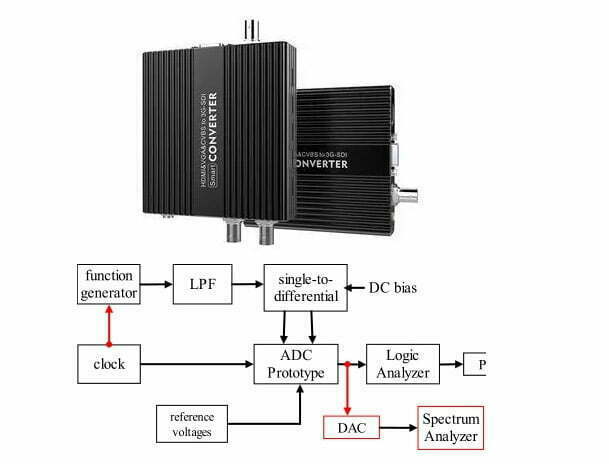
Unter den intelligenten Instrumenten spielen ADC- und DAC-Wandler eine zentrale Rolle. Wir wissen, dass die derzeit weit verbreiteten Mikroprozessoren nur mit diskreten digitalen Signalen umgehen können. Ohne einen ADC gibt es keine Möglichkeit, ein kontinuierliches analoges Signal aus der physikalischen Welt in einen Mikroprozessor einzuspeisen. Außerdem gibt es ohne einen DAC keine Möglichkeit, ein analoges Signal aus einem Mikroprozessor auszugeben. (Klicken Sie hier, um mehr über digitale Signale und analoge Signale zu erfahren.)
Analog-Digital-Wandler (ADC)
Definition von ADC
Im Messsystem ist es oft notwendig, die erfassten, sich ständig ändernden analogen Größen wie Temperatur, Druck, Durchfluss, Geschwindigkeit, Lichtintensität usw. in diskrete digitale Größen umzuwandeln, bevor sie zur Verarbeitung in den Computer eingegeben werden. Diese analogen Größen werden von Sensoren in elektrische Signale (in der Regel Spannungssignale) umgewandelt und müssen nach der Verstärkung durch Verstärker einer bestimmten Verarbeitung unterzogen werden, um zu digitalen Größen zu werden. Ein Gerät, das analoge in digitale Werte umwandelt, wird in der Regel als Analog-Digital-Wandler (ADC) oder kurz A/D bezeichnet.
Funktionsprinzip des ADC
Unter normalen Umständen muss die A/D-Wandlung im Allgemeinen vier Prozesse durchlaufen: Abtastung, Halten, Quantisierung und Codierung.
Probenahme und Aufbewahrung
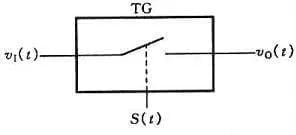
Abtastung bedeutet, eine analoge Größe, die sich kontinuierlich mit der Zeit ändert, in eine zeitdiskrete analoge Größe umzuwandeln. Das schematische Diagramm des Abtastvorgangs ist in Abbildung 1 dargestellt. Abbildung (a) zeigt den Aufbau einer Abtastschaltung, in der das Übertragungsgatter durch das Abtastsignal S(t) gesteuert wird. Während der Impulsbreite τ von S(t) ist das Übertragungsgatter eingeschaltet, das Ausgangssignal vO(t) ist das Eingangssignal v1, und während (Ts-τ) ist das Übertragungsgatter geschlossen und das Ausgangssignal vO(t)=0. Die Signalverläufe in der Schaltung sind in Abbildung (b) dargestellt.
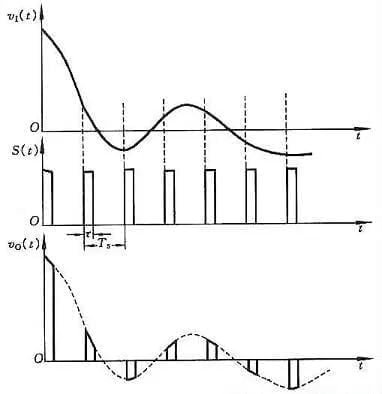
Aus der Analyse geht hervor, dass das erhaltene Signal das Eingangssignal nach dem Durchlaufen des Tiefpassfilters umso originalgetreuer wiedergeben kann, je höher die Frequenz des Abtastsignals S(t) ist. Das Problem dabei ist jedoch, dass die Datenmenge zunimmt. Um eine angemessene Abtastfrequenz zu gewährleisten, muss das Abtasttheorem erfüllt sein.
Abtasttheorem: Angenommen, die Frequenz des Abtastsignals S(t) beträgt fs und die Frequenz der höchsten Frequenzkomponente des analogen Eingangssignals v1(t) beträgt fimax, dann müssen fs und fimax die folgende Beziehung erfüllen: fs≥2fimax, wobei fs> in der Technik im Allgemeinen (3~5) fimax beträgt.
Es dauert eine gewisse Zeit, um das vom Abtastkreis erhaltene analoge Signal jedes Mal in ein digitales Signal umzuwandeln. Um einen stabilen Wert für den nachfolgenden Quantisierungs- und Codierungsprozess zu liefern, muss das jedes Mal erhaltene analoge Signal für einen bestimmten Zeitraum vom Halteschaltkreis gehalten werden.
Der Abtast- und Halteprozess wird häufig gleichzeitig durch die Abtast-Halte-Schaltung durchgeführt. Das schematische Diagramm und die Ausgangswellenform der Abtast-Halte-Schaltung sind in Abbildung 2 dargestellt.
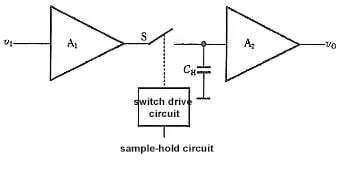
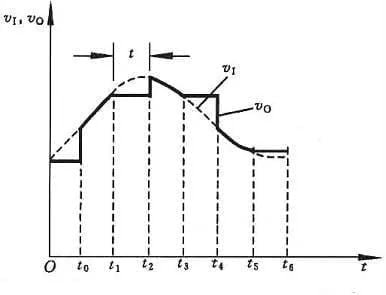
Die Schaltung besteht aus einem Eingangsverstärker A1, einem Ausgangsverstärker A2, einem Haltekondensator CH und einer Schaltansteuerschaltung. A1 muss eine hohe Eingangsimpedanz in der Schaltung aufweisen, um den Einfluss auf die Eingangssignalquelle zu verringern. Um die Entladung der auf CH gespeicherten Ladung während der Haltephase zu erschweren, sollte A2 ebenfalls eine hohe Eingangsimpedanz aufweisen, und A2 sollte außerdem eine niedrige Ausgangsimpedanz haben, wodurch die Belastbarkeit der Schaltung verbessert werden kann. Im Allgemeinen ist außerdem erforderlich, dass AV1·AV2=1 in der Schaltung gilt.
Analysieren wir nun anhand von Abbildung 2 die Funktionsweise der Schaltung. Bei t=t0 ist der Schalter S geschlossen und der Kondensator wird schnell aufgeladen. Da AV1 · AV2=1, v0=vI, liegt die Abtastperiode im Zeitintervall von t0 bis t1. Zum Zeitpunkt t=t1 wird S getrennt. Wenn die Eingangsimpedanz von A2 unendlich ist und S ein idealer Schalter ist, kann davon ausgegangen werden, dass der Kondensator CH keinen Entladungskreis hat und die Spannung an seinen beiden Enden konstant bei v0 bleibt. Der flache Abschnitt von t1 bis t2 in Abbildung 11.8.2(b) ist die Haltephase.
Die Sample-Hold-Schaltung kann durch verschiedene Arten von monolithischen integrierten Schaltungen hergestellt werden. Beispielsweise gibt es AD585 und AD684 für die bipolare Technologie sowie AD1154 und SHC76 für die gemischte Technologie.
Quantisierung und Codierung
Digitale Signale sind nicht nur zeitlich diskret, sondern auch in ihrer Amplitude unstetig. Die Größe einer digitalen Größe kann nur ein ganzzahliges Vielfaches einer festgelegten Mindestgrößeneinheit sein. Um das analoge Signal in eine digitale Größe umzuwandeln, muss im A/D-Wandlungsprozess die Ausgangsspannung der Sample-Hold-Schaltung ebenfalls auf eine bestimmte annähernde Weise auf den entsprechenden diskreten Pegel normiert werden. Dieser Umwandlungsprozess wird als Quantisierung bezeichnet. Die Quantifizierung wird als Quantisierung bezeichnet. Der quantisierte Wert muss schließlich durch den Codierungsprozess durch einen Code dargestellt werden. Der nach der Codierung erhaltene Code ist die vom A/D-Wandler ausgegebene digitale Größe.
Die kleinste Mengeneinheit, die im Quantisierungsprozess verwendet wird, wird als Quantisierungseinheit bezeichnet und durch △ dargestellt. Es handelt sich um die analoge Größe, die dem niedrigsten Bit des digitalen Signals entspricht, wenn dieses 1 ist, d. h. 1 LSB.
Da die Abtastspannung im Quantisierungsprozess nicht unbedingt durch △ teilbar ist, kommt es zwangsläufig zu einem Fehler vor und nach der Quantisierung. Dieser Fehler wird als Quantisierungsfehler bezeichnet und durch ε dargestellt. Der Quantisierungsfehler ist ein grundsätzlicher Fehler, der nicht beseitigt werden kann. Je mehr Bits der A/D-Wandler hat, desto geringer ist der Unterschied zwischen den diskreten Pegeln und desto geringer ist der Quantisierungsfehler.
Im Quantisierungsprozess werden häufig zwei approximative Quantisierungsmethoden verwendet: nur Rundungsquantisierung und Rundungsquantisierung.
nur Aufrunden der Quantisierungsmethode
Nehmen wir als Beispiel den 3-Bit-A/D-Wandler, wobei das Eingangssignal v1 im Bereich von 0 bis 8 V liegt. Bei Verwendung der Aufrundungsquantisierungsmethode nehmen wir △=1 V und verwerfen den Teil, der nicht in die Quantisierungseinheit passt. Liegt der Wert zwischen 0 und 8 V, wird die analoge Spannung zwischen 1 V als 0△ betrachtet, dargestellt durch die Binärzahl 000, und die analoge Spannung zwischen 1 V und 2 V wird als 1△ betrachtet, dargestellt durch die Binärzahl 001… Der maximale Fehler dieser Quantisierungsmethode beträgt △.
Rundungsquantisierungsverfahren
Wenn die Rundungsquantisierungsmethode angewendet wird, wird die Quantisierungseinheit △=8V/15 verwendet, und der Teil, der weniger als die Hälfte der Quantisierungseinheit beträgt, wird während des Quantisierungsprozesses verworfen, während der Teil, der gleich oder größer als die Hälfte der Quantisierungseinheit ist, als eine Quantisierungseinheit behandelt wird. Die analoge Spannung zwischen 0 und 8 V/15 wird als 0△ behandelt, dargestellt durch die Binärzahl 000, und die analoge Spannung zwischen 8 V/15 und 24 V/15 wird als 1△ behandelt, dargestellt durch die Binärzahl 001, was „Warten” bedeutet.
Vergleich
Der maximale Quantisierungsfehler │εmax│=1LSB beim erstgenannten Quantisierungsverfahren mit nur Rundung und der Quantisierungsfehler │εmax│=1LSB/2 beim zweitgenannten Quantisierungsverfahren mit Rundung und Rundung – der Quantisierungsfehler des zweitgenannten Verfahrens ist kleiner als der des erstgenannten, weshalb es bei den meisten A/D-Wandlern zum Einsatz kommt.
Mit der rasanten Entwicklung integrierter Schaltkreise entstehen ständig neue Designideen und Fertigungstechniken für A/D-Wandler. A/D-Wandler mit unterschiedlichen Strukturen und Leistungen werden entwickelt, um verschiedenen Erfassungs- und Steuerungsanforderungen gerecht zu werden.
Arten von ADC
Integration von ADC
Umwandlungsprinzip
Das Umwandlungsprinzip des integrierenden ADC basiert auf der Integration der Spannung und dem Vergleich der integrierten Spannung mit einer anderen Spannung, um den Zählwert zu steuern. Der Zählwert ist der Ausgang des ADC. Das Objekt der Integration basiert entweder auf der Referenzspannung oder auf der Referenzspannung und der Eingangsspannung.
Vor- und Nachteile
Vorteile:
- Der integrierte ADC hat eine hohe Auflösung, und die Anzahl der Stellen kann 12 oder sogar mehr betragen.
- Die Linearität ist sehr gut. Im Wesentlichen wird der Eingang mit einer integrierten Referenzspannung verglichen, um den Ausgang zu bestimmen, sodass die Linearität von der Genauigkeit des Komparators abhängt.
- Die Topologie der Schaltungsrealisierung ist einfach, und es werden relativ wenige Komponenten zur Realisierung dieser Bauelemente verwendet, sodass die Schaltung relativ einfach und die Produktionskosten gering sind.
Nachteil:
- Der Hauptnachteil ist die langsame Wandlungsgeschwindigkeit. Bei einem N-Bit-ADC kann die Ausgabe bis zu 2 N Taktzyklen benötigen, um einen einzelnen Abtastpunkt zu wandeln.
Anwendungen
Wird hauptsächlich in Sensoranwendungen und Geräten wie Voltmetern und Amperemetern verwendet, bei denen Genauigkeit wichtiger ist als Geschwindigkeit. Mit anderen Worten: Die Abtastgeschwindigkeit des integrierten ADC ist relativ niedrig, aber die Genauigkeit ist sehr hoch.
Klassifizierung
Es gibt verschiedene Arten von Integral-ADCs, wobei die gängigsten Single- und Double-Slope-Integrale sind. Durch Hinzufügen einer „Steigung” wird die Genauigkeit erhöht, was jedoch zu Lasten der Umwandlungszeit geht.
Einfach geneigter Integral-ADC
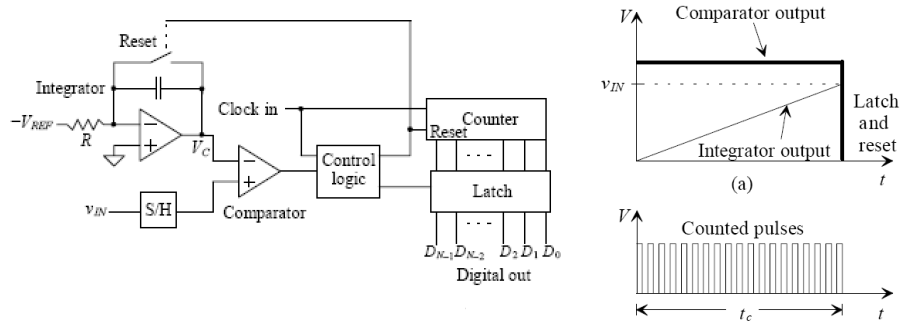
Der Komparator vergleicht die Eingangsspannung mit dem Wert der integrierten Referenzspannung (beachten Sie, dass wir diesen negativ machen, da er mit dem invertierenden Eingang des Operationsverstärkers verbunden ist). Gleichzeitig wird die Anzahl der Taktzyklen gezählt. Wenn der Ausgang des Integrators gleich ist, gibt der Komparator eine logische „0“ aus, wodurch ein Reset des Zählers und des Integrators ausgelöst wird, und der Latch hält den digitalen Ausgang.
VINVREFVrefVrefVin
Dies ist die Umwandlungszeit. Ich weiß, warum dieser integrierte ADC langsam ist. Betrachten wir den ungünstigsten Fall, angenommen die Eingangsspannung beträgt , angenommen , angenommen es handelt sich um einen 20-Bit-ADC, dann!
VIN=VREFTCLK=1ustc=220us=1048576us
Einfach geneigter Integral-ADC
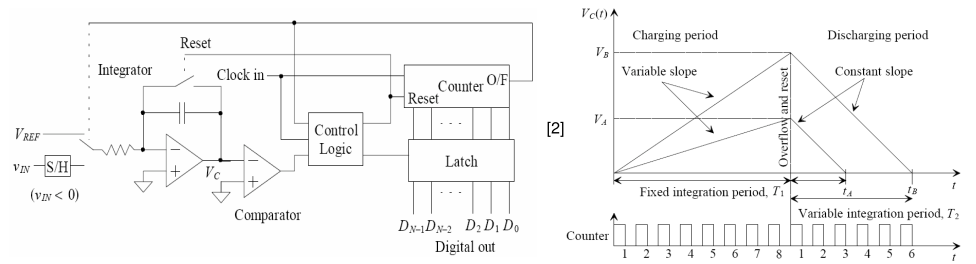
Ein Dual-Slope-ADC unterscheidet sich von einem Single-Slope-ADC dadurch, dass nun der Vergleich mit Masse erfolgt und zwei Spannungssummen integriert werden. Zu Beginn wird der negative Eingang an den Integrator angeschlossen, der so lange ansteigt, bis der Zähler überläuft. Da die Integration am invertierenden Eingang zu einem negativen Wert wechselt, ist der Ausgang des Integrators immer positiv und größer als Null, sodass der Zähler so lange läuft, bis er überläuft, was 2N Taktzyklen (=T1) dauert.
VCVREFVINVC
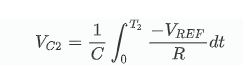
Zum Zeitpunkt T2 entspricht sie der Summe aus und und
VC=VC1+VC2=0
Aber:
VIN/VREF=T2/T1
Daher ist das Prinzip der ADC-Wandlung, Dual-Slope-ADC, langsamer als Single-Slope-ADC, da die Integration zweimal durchgeführt wird, wodurch der Fehler in Bezug auf die Steigung des Integrators aufgehoben wird, was grundsätzlich die Genauigkeit verbessert.
Sigma-Delta Σ-Δ ADC
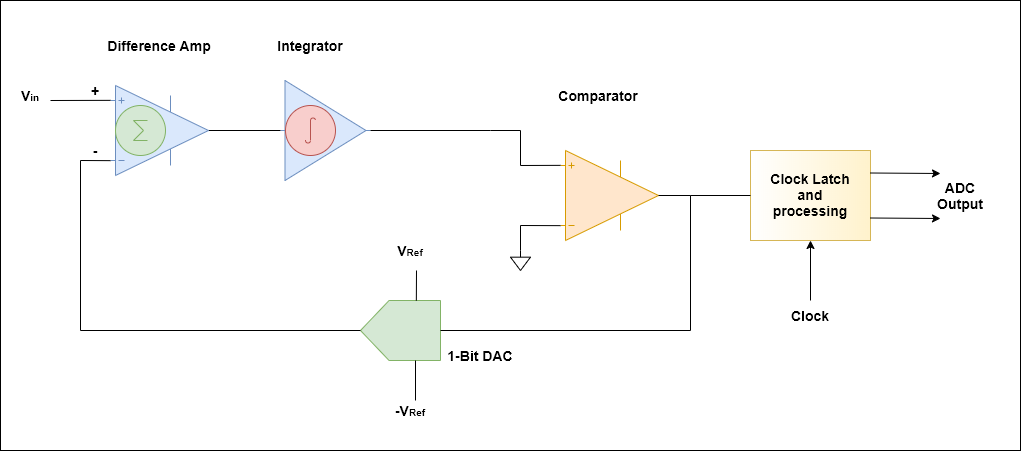
Ausgehend vom Eingang erzeugt der Differenzverstärker einen Ausgang, der der Differenz zwischen Vin und dem 1-Bit-DAC-Ausgang entspricht. Der Ausgang eines 1-Bit-DAC kann einen von zwei Werten annehmen: OR . In dieser Topologie kann man sich einen Integrator als einen gleitenden Durchschnitt des vorherigen Werts und des aktuellen Eingangswerts vorstellen.
–Vref+Vref
Unter der Annahme, dass das positive Segment des Komparators anfänglich auf einen kleinen Wert über 0 V festgelegt ist, kehrt sich der Komparator um. Sein Wert ist hoch oder 1. Dann ist der DAC-Ausgang . Bei der nächsten Iteration wird dieser Wert vom aktuellen Wert von subtrahiert. Da der vorherige Wert 0 V war, ist der Integratorausgang nun – Vref. Zu diesem Zeitpunkt ist der Komparatorausgang 0 und der DAC-Ausgang.
+VrefVin-Vref
Bei der nächsten Abtastung ist der Integratorausgang aufgrund des vorherigen Werts 0, und der Differenzverstärker subtrahiert tatsächlich , wodurch zu addiert wird. Der Komparatorausgang ist 1.
-Vref-Vref+VrefVin
Dieser Vorgang wiederholt sich iterativ, sodass bei einer Eingabe von 0 V die Ausgabe des Komparators ein stetiger Strom von 101010… ist. Denken Sie daran, dass logisch 1 bedeutet und logisch 0 bedeutet. Wenn also N Abtastwerte abgetastet und gemittelt werden, ist es leicht zu erkennen, dass der Durchschnittswert 0 V beträgt. Der Verarbeitungsblock nach dem Komparator gibt dies einfach als einen einzigen Wert 0000… aus, wobei ein Referenzwert von ( ~ ) oder 2 x angenommen wird.
+Vref-Vref-Vref+VrefVref
Angenommen, 1 V, dann handelt es sich um einen 5-V-ADC. ist ±2,5 V. Wenn man die gleichen Schritte wie zuvor iterativ durchführt, lautet die Ausgabe: 1011101… Die Ausgabe beträgt 1,07 V.
Vin±Vref
Zusammenfassend:
Ein Sigma-Delta-ADC überabtastet das zu verarbeitende Signal (siehe „Analog-Digital-Abtastung“ für dieses Konzept) und filtert das zu verarbeitende Signal mit einem Tiefpassfilter. In der Regel ist die Anzahl der mit dem Flash-ADC nach dem Filter konvertierten Bits geringer als die erforderliche Anzahl von Bits. Das resultierende Signal wird zusammen mit den Fehlern aus den diskreten FLASH-Pegeln zurückgeführt, vom Eingang subtrahiert und dem Filter zugeführt. Diese negative Rückkopplung dämpft das Rauschen, sodass es nicht bei der gewünschten Signalfrequenz auftritt. Ein Digitalfilter nach dem ADC (unter Verwendung eines Dezimierungsfilters) reduziert die Abtastrate, filtert unerwünschte Rauschsignale heraus und erhöht die Ausgangsauflösung (daher der Name Sigma-Delta-Modulation, auch bekannt als Delta-Sigma-Modulation).
Flash-ADC (Direktvergleichstyp)
Das Prinzip des FLASH-ADC ist vielleicht am einfachsten zu verstehen. Die folgende Abbildung zeigt ein schematisches Diagramm eines 2-Bit-ADC, der aus vielen Komparatoren besteht, von denen jeder mit einer Referenzspannung versorgt wird, die um ein Bit höher ist als der vorherige Referenzwert. Für einen 8-Bit-ADC sind daher 256 solcher Komparatoren erforderlich. Für 10 Bit benötigen Sie 1024.
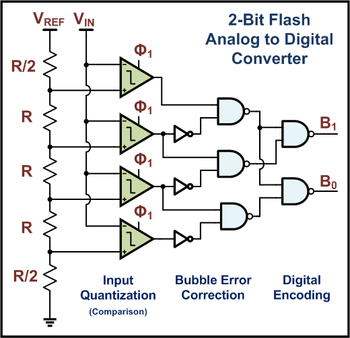
LASH-ADC (Direktvergleichstyp) ist schnell. Er wandelt die Eingabe direkt um, ohne dass eine Abtastung oder aufwendige Nachbearbeitung erforderlich ist. Das Problem dabei ist, dass dafür viele Komparatoren benötigt werden, die viel Platz auf dem Chip einnehmen. Verwenden Sie Fash-ADCs daher nur, wenn Sie extrem hohe Geschwindigkeiten benötigen, die mit anderen ADC-Implementierungen nicht erreicht werden können.
In Hardware verkörperte Dichotomie
In der Praxis gibt es eine weitere Variante, die häufiger verwendet wird, den Semi-FLASH-ADC. Er nutzt einen zweistufigen Prozess, um die Anzahl der in der eigentlichen Wandlerkette benötigten Wandler zu reduzieren:
Zunächst wird das Eingangssignal mit den Pegelwerten verglichen, die genau in der Mitte liegen. Ist es niedriger, wird das höchstwertige Bit (MSB) auf 0 gesetzt und der Eingang wird an eine Kette von Komparatoren mit der Referenzspannung weitergeleitet, um die restlichen Bits umzuwandeln.
Wenn das Eingangssignal über liegt, wird das MSB auf 1 gesetzt und vom Eingangssignal subtrahiert. Die Komparatorenkette wird erneut verwendet, um die restlichen Bits zu erhalten. Im Wesentlichen verzichtet der Halbschritt-FLASH-ADC also auf einen zusätzlichen Vergleich, um die Hälfte des Komparators einzusparen. Diese Art des Denkens lässt sich auch weiter ableiten und ausbauen, beispielsweise zum 4-Punkt-FLASH-ADC und so weiter.
Das sukzessive Approximationsregister (SAR)
Das Successive Approximation Register (SAR) ist ein integraler Bestandteil des sukzessiven Approximations-ADCs. Es nutzt einen Komparator, um den Bereich, der die Eingangsspannung enthält, schrittweise einzugrenzen. Dazu vergleicht der Wandler die Eingangsspannung mit dem Ausgang eines Digital-Analog-Wandlers, der in der Regel die Mitte des gewählten Spannungsbereichs angibt. Bei jedem Schritt des Prozesses wird die Schätzung im SAR gespeichert.
Nehmen wir beispielsweise an, die Eingangsspannung beträgt 6,3 V und der anfängliche Bereich liegt zwischen 0 und 16 V.
- Im ersten Schritt werden 6,3 V eingegeben, um sie mit 8 V (dem Mittelpunkt des Bereichs von 0 bis 16 V) zu vergleichen. Der Komparator meldet eine Eingangsspannung von weniger als 8 V, sodass der SAR aktualisiert wird, um den Bereich auf 0 bis 8 V zu reduzieren.
- Im zweiten Schritt wird die Eingangsspannung mit 4 V (dem Mittelpunkt von 0 bis 8 V) verglichen. Der Komparator meldet, dass die Eingangsspannung über 4 V liegt, sodass der SAR aktualisiert wird, um widerzuspiegeln, dass die Eingangsspannung im Bereich von 4 bis 8 V liegt.
- Im dritten Schritt wird die Eingangsspannung mit 6 V (der Hälfte von 4 V bis 8 V) verglichen; der Komparator meldet eine Eingangsspannung von mehr als 6 Volt, und der Suchbereich wird auf 6 bis 8 Volt festgelegt.
Wiederholen Sie diese Schritte, bis Sie die gewünschte Lösung erreichen. Die Topologie sieht wie folgt aus:
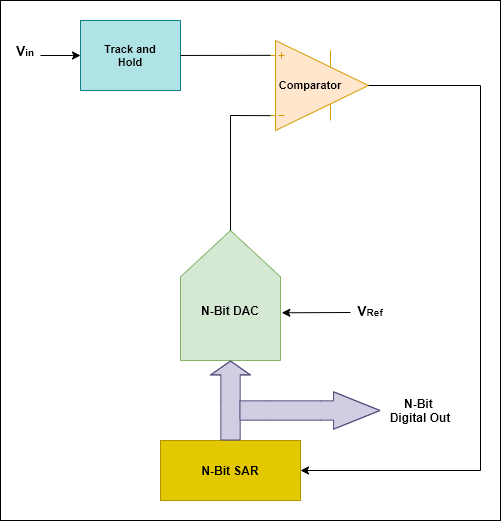
Zur Veranschaulichung sehen Sie sich bitte die folgende Animation an:
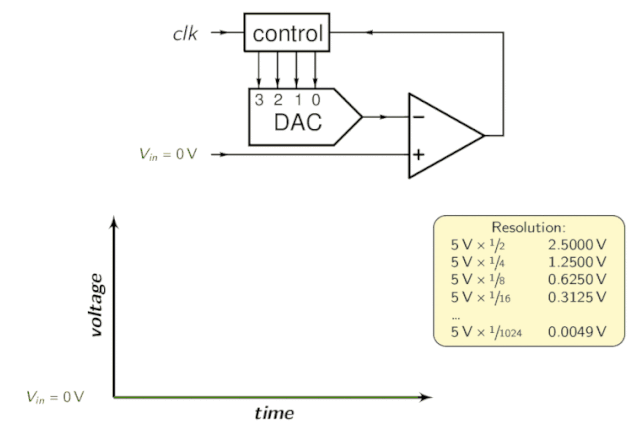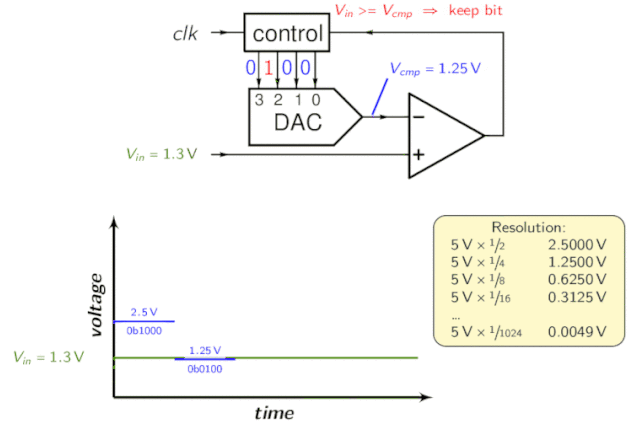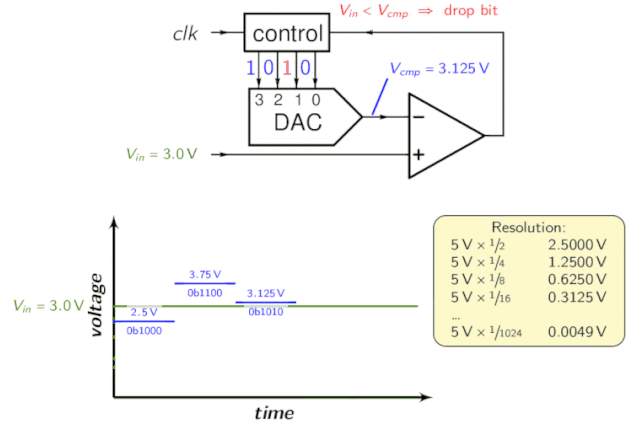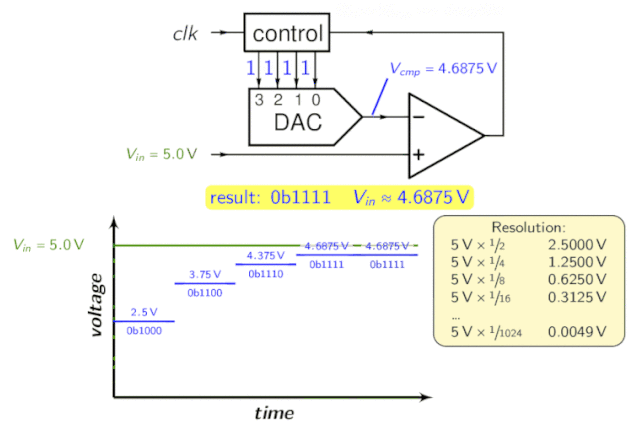
Pipelined-ADC
Ein Pipeline-ADC (auch als Subroutine-Quantisierer bekannt) verwendet zwei oder mehr Pipelines. Zunächst wird eine grobe Umwandlung durchgeführt. Im zweiten Schritt wird ein Digital-Analog-Wandler (DAC) verwendet, um die Differenz im Eingangssignal zu bestimmen. Diese Differenz wird dann in feinere Werte umgewandelt und die Ergebnisse werden in einem letzten Schritt kombiniert. Dies kann als Verbesserung gegenüber nachfolgenden Approximations-ADCs angesehen werden, bei denen das Rückkopplungsreferenzsignal aus Zwischenübergängen über den gesamten Bitbereich (z. B. 4 Bit) besteht und nicht nur aus dem nächsthöheren Bit. Dieser Typ vereint die Vorteile der sukzessiven Approximationsmethode und des Flash-ADCs und zeichnet sich durch hohe Geschwindigkeit, hohe Auflösung und geringe Baugröße aus.
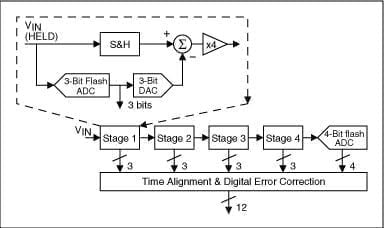
In diesem Schaltplan wird der analoge Eingang VIN zunächst durch einen Sample-and-Hold-Schaltkreis (S&H) abgetastet und stabil gehalten, während der Flash-ADC in der ersten Stufe ihn auf drei Bit quantisiert. Der 3-Bit-Ausgang wird dann an einen 3-Bit-DAC (12-Bit-Genauigkeit) weitergeleitet und der analoge Ausgang vom Eingang subtrahiert. Dieser „Rest” wird um den Faktor 4 vergrößert und an die nächste Stufe (Stufe 2) weitergeleitet. Dieser hinzugefügte Rest wird durch die unteren Stufen der Pipeline weitergeleitet und liefert 3 Bit pro Stufe, bis er den 4-Bit-Flash-ADC erreicht, der die letzten 4 LSB-Bits auflöst. Da die Bits für jede Stufe zu unterschiedlichen Zeitpunkten bestimmt werden, werden alle Bits, die derselben Abtastung entsprechen, mit dem Schieberegister zeitlich abgeglichen, bevor sie an die digitale Fehlerkorrekturlogik weitergeleitet werden. Beachten Sie, dass eine Pipeline, nachdem sie die Verarbeitung der Eingangsabtastwerte abgeschlossen, das Erfassungsbit für diese Pipeline bestimmt und den Rest an die nächste Pipeline weitergeleitet hat, mit der Verarbeitung des nächsten Abtastwerts beginnen kann, der vom in jeder Pipeline eingebetteten Abtastwertspeicher empfangen wird. Diese Pipeline-Verarbeitung ist der Grund für den hohen Durchsatz, der auch das Konzept der Pipeline-Verarbeitung ausmacht.
Andere
Zusätzlich zu den oben genannten gängigen ADCs gibt es auch ADCs nach dem Ladungsausgleichsprinzip, Time-Sharing-ADCs, FM-ADCs, Time-Stretching-ADCs, inkrementelle Kodierungs-ADCs, Wilkinson-ADCs usw.
Digital-Analog-Wandler (DAC)
Definition von DAC
Die vom digitalen System verarbeitete digitale Größe muss manchmal für die praktische Verwendung in eine analoge Größe umgewandelt werden. Diese Umwandlung wird als „Digital-Analog-Wandlung” bezeichnet. Die Schaltung, die die Digital-Analog-Wandlung durchführt, wird als Digital-Analog-Wandler oder kurz DAC (Digital to Analog Converter) bezeichnet.
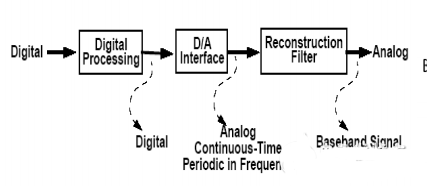
DAC-Parameter
Auflösung
Die Auflösung in DAC wird definiert als die Anzahl aller möglichen analogen Ausgangspegel unter verschiedenen digitalen Eingangswertcodes. Eine N-Bit-Auflösung bedeutet, dass DAC 2 N −1 verschiedene analoge Pegel erzeugen kann. Im Allgemeinen bezieht sich dies auf die Anzahl der Stellen des digitalen Eingangswertcodes.
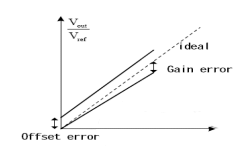
Offset- und Verstärkungsfehler
Der Offset ist definiert als der Wert des tatsächlichen analogen Ausgangssignals, wenn ein Codewert von 0 eingegeben wird, und der Verstärkungsfehler ist definiert als die Differenz zwischen dem idealen Vollausgangswert und dem tatsächlichen Ausgangswert nach Abzug des Offsets, wie in der Abbildung dargestellt.
Genauigkeit
Die Genauigkeit in DAC wird in absolute Genauigkeit und relative Genauigkeit unterteilt. Die absolute Genauigkeit ist definiert als die Differenz zwischen der idealen Ausgabe und der tatsächlichen Ausgabe, einschließlich verschiedener Offset- und nichtlinearen Fehler. Die relative Genauigkeit ist definiert als der maximale integrale nichtlineare Fehler. Die Genauigkeit wird als Verhältnis des Skalenendwerts ausgedrückt, angegeben in effektiven Stellen. Eine Genauigkeit von 8 Bit bedeutet beispielsweise, dass der Fehler des DAC weniger als 1/8 2 des Vollausgangs des DAC beträgt. Beachten Sie, dass das Konzept der Genauigkeit nicht mit der Auflösung zusammenhängt. Ein DAC mit einer Auflösung von 12 Bit kann nur eine Genauigkeit von 10 Bit haben, und ein DAC mit einer Auflösung von 10 Bit kann eine Genauigkeit von 12 Bit haben. Genauigkeit vor Auflösung bedeutet, dass die Übertragungsantwort des DAC präziser gesteuert werden kann.
INL-Integral-Nichtlinearität
Wenn Offset- und Verstärkungsfehler beseitigt sind, wird der integrale Linearitätsfehler als Abweichung der tatsächlichen Ausgangstransfercharakteristik von der idealen Transfercharakteristik (einer geraden Linie) definiert, wie in der Abbildung dargestellt.
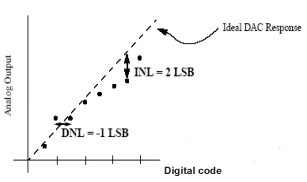
DNL-Differential-Nichtlinearität
In einem idealen DAC mit mindestens 1 LSB pro analoger Ausgangsänderung wird der differentielle Linearitätsfehler als Abweichung von 1 LSB pro minimaler analoger Ausgangsänderung definiert (ohne Verstärkungsfehler und Offset). Der von uns definierte DNL gilt für jeden digitalen Eingangs-Codewert, und manchmal wird der größte DNL verwendet, um den DNL des gesamten DAC zu definieren. Ein idealer DAC hätte einen differentiellen Linearitätsfehler von Null für jeden digitalen Eingang, während ein DAC mit einem maximalen DNL von 0,5 LSB eine minimale Ausgangsänderung zwischen 0,5 LSB und 1,5 LSB pro Ausgang hätte. Die integralen und differentiellen Linearitätsfehler des DAC sind in der Abbildung dargestellt.
Jitter-Energie (Glitch-Impulsfläche)
Die maximale Fläche unter dem Jitter, der nach einer Änderung des Eingangssignals am Ausgang auftritt.
Ablagerungszeit
Die Einschwingzeit liegt innerhalb eines bestimmten Fehlerbereichs des Endwerts und ist die Zeit, die benötigt wird, bis die Ausgabe die volle Skalierung erreicht hat.
Monotonie Ein monotoner DAC ist ein DAC, bei dem der analoge Ausgangspegel immer mit steigendem digitalen Eingangswert zunimmt. Wenn die maximale DNL innerhalb von 0,5 LSB gehalten wird, kann die Monotonie des DAC auf natürliche Weise gewährleistet werden.
Spurious Dynamic Range (SFDR) SFDR steht für Spurious Free Dynamic Range, also den Dynamikbereich ohne Rauschen und Oberwellen. Sowohl Rauschen als auch Oberwellen werden als Störsignale bezeichnet.
Prinzip des DAC
Wandeln Sie jeden eingegebenen Binärcode entsprechend seinem Gewicht in eine entsprechende analoge Größe um und addieren Sie dann die analogen Größen, die jedes Bit darstellen. Die erhaltene analoge Gesamtgröße ist proportional zur digitalen Größe, wodurch die Umwandlung von einer digitalen Größe in eine analoge Größe realisiert wird. Analoge Umwandlung.
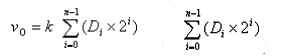
Es handelt sich um den Dezimalwert, der durch Bitgewichtserweiterung in eine Binärzahl umgewandelt wurde.
Zusammensetzung und Eigenschaften von DAC
Der DAC besteht hauptsächlich aus digitalen Registern, analogen elektronischen Schaltern, einem Bitgewichtungsnetzwerk, einem Summierverstärker und einer Referenzspannungsquelle (oder einer Konstantstromquelle). Verwenden Sie die Ziffern der im digitalen Register gespeicherten digitalen Größen, um die analogen elektronischen Schalter der entsprechenden Ziffern jeweils zu steuern, sodass die Ziffer mit der Ziffer 1 einen Stromwert erzeugt, der proportional zu ihrem Zifferngewicht im Zifferngewichtungsnetzwerk ist, und dann steuert der Operationsverstärker jeden Stromwert, der summiert und in einen Spannungswert umgewandelt wird.
Durch Variieren der Bitgewichtungsnetzwerke können verschiedene Arten von DACs zusammengebaut werden, darunter der DAC mit Gewichtswiderstandsnetzwerk, der DAC mit R-2R-invertiertem T-förmigem Widerstandsnetzwerk und der DAC mit Einzelwert-Stromnetzwerk usw. Die Genauigkeit der durch den DAC mit Gewichtswiderstandsnetzwerk erzeugten Umwandlung hängt von der Genauigkeit der Referenzspannung VREF sowie von der Qualität der analogen elektronischen Schalter, Operationsverstärker und Gewichtswiderstandswerte ab. Sein Nachteil besteht darin, dass die Widerstandswerte der einzelnen Gewichtswiderstände unterschiedlich sind und bei vielen Stellen die Widerstandswerte stark variieren, was die Gewährleistung der Genauigkeit erheblich erschwert, insbesondere bei der Herstellung von integrierten Schaltkreisen. Daher wird diese Schaltung in integrierten DACs selten allein verwendet.
Wichtigste technische Indikatoren des DAC
Wandlungsgenauigkeit und Wandlungsgeschwindigkeit von DAC: Die Wandlungsgenauigkeit wird im Allgemeinen durch die Auflösung und den Wandlungsfehler im DAC beschrieben.
Auflösung
Im Allgemeinen wird die Anzahl der Bits des DAC zur Messung der Auflösung verwendet, da je höher die Anzahl der Bits ist, desto mehr Werte (2n) der Ausgangsspannung vO vorhanden sind und desto besser die subtilen Änderungen der Ausgangsspannung wiedergegeben werden können.
Darüber hinaus kann die Auflösung auch durch das Verhältnis der minimalen Ausgangsspannung 1 LSB, die der DAC unterscheiden kann, zur maximalen Ausgangsspannung FSR definiert werden. Diese lautet:
Auflösung = 1 LSB/FSR = k/k(2n-1) = 1/(2n-1)
Je kleiner der Wert, desto höher die Auflösung.
Konvertierungsfehler
Der Umwandlungsfehler ist die maximale Abweichung zwischen der tatsächlichen analogen Ausgangsspannung und dem Idealwert. Er wird üblicherweise als Prozentsatz oder als mehrere LSBs des Verhältnisses dieser maximalen Abweichung zum FSR ausgedrückt. Tatsächlich handelt es sich dabei um einen umfassenden Indikator für die drei Fehler.
Umwandlungsgeschwindigkeit
Die Umwandlungsgeschwindigkeit wird im Allgemeinen durch die Einschwingzeit bestimmt. Der Zeitraum zwischen dem Zeitpunkt, zu dem sich der Eingang von allen Nullen zu allen Einsen ändert, und dem Zeitpunkt, zu dem sich die Ausgangsspannung innerhalb des Bereichs von FSR±½ LSB (oder dem durch FSR±x%FSR angegebenen Bereich) stabilisiert, wird als Einschwingzeit bezeichnet. Dies ist die maximale Reaktionszeit des DAC. Verwenden Sie diesen Wert daher zur Messung der Umwandlungsgeschwindigkeit.
Arten von DAC
Widerstandstyp
Die Struktur ist in Abbildung 1 dargestellt. Abbildung 1 zeigt einen Wandler vom Typ R-2R-Leiternetzwerk. Sein Vorteil besteht darin, dass er eine sehr gute Linearität erzielen kann. Da alle Stromquellen gleichwertig sind, können wir spezielle zusätzliche Technologien einsetzen, um den Fehler zwischen ihnen zu verringern, und seine Struktur ist viel einfacher als die eines Widerstandsteilers. Der Nachteil ist, dass der Widerstand immer nichtlinear ist und er auch parasitäre Kapazitäten enthält, die mit dem Signal zusammenhängen, sodass es schwierig ist, eine vollständige Anpassung zu erreichen. Gleichzeitig wird die Geschwindigkeit durch den Ausgangsbuffer begrenzt und kann nicht sehr hoch sein.
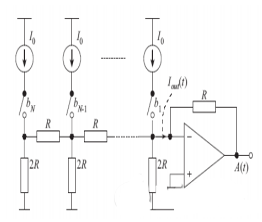
Kapazitiver Typ
Die Struktur ist in Abbildung 2 dargestellt. Die Kapazität höchster Ordnung CN ist 1 2N− mal so groß wie die Kapazität niedrigster Ordnung C1. Der Vorteil besteht darin, dass der Stromverbrauch gering ist und die Anpassungsgenauigkeit höher ist als bei einem Widerstand. Die wichtigsten begrenzenden Faktoren sind die Fehlanpassung der Kondensatoren, der Einschaltwiderstand der Schalter, große RC-Verzögerungen und der Einfluss der begrenzten Bandbreite des Verstärkers auf die Geschwindigkeit des DAC. Ein großer Nachteil von DACs mit Ladungsverteilung ist, dass Kondensatoren in CMOS-Prozessen viel Chipfläche für die Implementierung beanspruchen. Da die Kapazität im CMOS-Prozess von Natur aus nichtlinear ist, wird schließlich die Linearität des gesamten DAC unterdrückt. Geeignet für mittlere und breite Bandbreiten mit hoher Präzision.
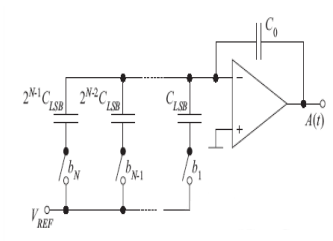
Aktueller Typ
Die Struktur ist in Abbildung 3 dargestellt. Der Vorteil besteht darin, dass bei einer Genauigkeit von weniger als 10 Bit die Fläche sehr klein gehalten werden kann und die Geschwindigkeit nicht durch die Bandbreite des Verstärkers und die große RC-Verzögerung begrenzt wird. Es kann eine sehr hohe Geschwindigkeit erreicht werden. Da der gesamte Strom direkt zum Ausgangsanschluss fließt, ist der Energieverbrauch sehr effizient und einfach zu realisieren. Die Nachteile sind die Empfindlichkeit gegenüber Gerätefehlanpassungen und die begrenzte Ausgangsimpedanz der Stromquelle. Geeignet für Anforderungen an hohe Geschwindigkeiten und große Bandbreiten.
Es ist auch möglich, keinen Operationsverstärker für den Ausgang zu verwenden und stattdessen direkt den Lastwiderstand zu nutzen, um den Strom in einen Spannungsausgang umzuwandeln, wie in Abbildung 4 dargestellt. Bei dieser Form wird die Rate des DAC nicht durch die Bandbreite des Operationsverstärkers begrenzt.
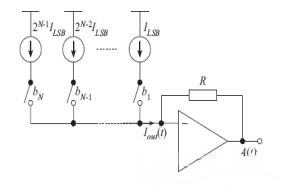
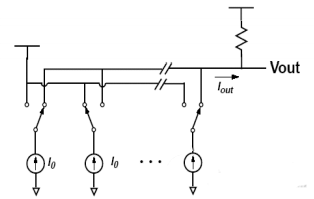
Typische Vermehrung
Einige DA-Wandler verwenden eine konstante Referenzspannung, andere fügen dem Referenzspannungseingang ein Wechselstromsignal hinzu. Letztere werden als Multiplikations-DA-Wandler bezeichnet, da sie das Ergebnis der Multiplikation des digitalen Eingangs und des Referenzspannungseingangs liefern können. Im Allgemeinen kann ein Multiplikations-DA-Wandler nicht nur Multiplikationen durchführen, sondern auch als Dämpfungsglied zur digitalen Dämpfung eines Eingangssignals und als Modulator zur Modulation eines Eingangssignals verwendet werden.
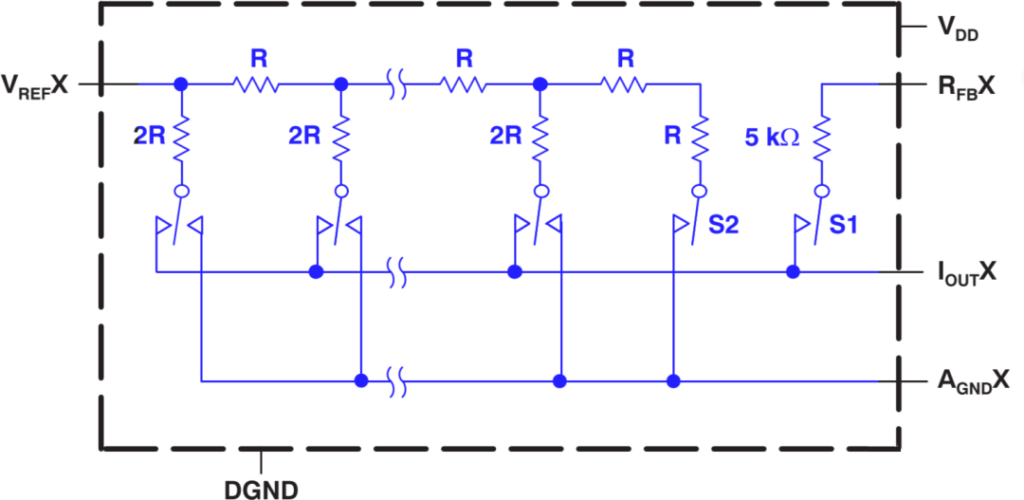
Ein DA-Wandler
Im Gegensatz zu dem gerade beschriebenen Wandlersystem verwendet ein DA-Wandler ein spezielles Verfahren, um digitale Werte in eine Pulsweitenmodulation oder Frequenzmodulation umzuwandeln, die dann mit einem digitalen Filter geglättet wird, um einen häufig verwendeten Spannungsausgang (auch als Bitstrommodus bekannt) für Audio usw. zu erzeugen.
Fazit
Der ADC- und DAC-Wandler sind zwei wesentliche Komponenten jedes digitalen Systems. Sie helfen dabei, analoge Signale in digitale Signale umzuwandeln und umgekehrt. Der ADC (Analog-Digital-Wandler) nimmt ein analoges Signal auf und wandelt es in ein digitales Signal um, während der DAC (Digital-Analog-Wandler) ein digitales Signal aufnimmt und es in ein analoges Signal umwandelt. Beide Komponenten sind für eine Vielzahl von Anwendungen wichtig, von der Audio- und Videoverarbeitung bis hin zur Datenübertragung. In diesem Artikel haben wir die Funktionsweise dieser Wandler und ihre Bedeutung in verschiedenen Anwendungen erläutert. Außerdem haben wir die verschiedenen Wandlertypen, die verschiedenen Signaltypen, die sie umwandeln können, sowie die Vor- und Nachteile der einzelnen Typen untersucht.