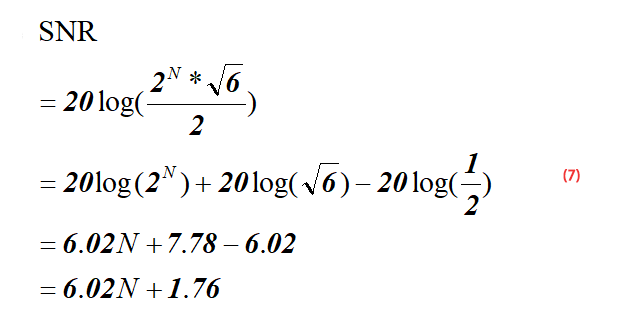Was ist das Signal-Rausch-Verhältnis?
Das Signal-Rausch-Verhältnis (SNR) ist ein in Wissenschaft und Technik verwendetes Maß, das den Pegel eines gewünschten Signals mit dem Pegel des Hintergrundrauschens vergleicht. Es ist definiert als das Verhältnis der Signalleistung zur Rauschleistung. Ein Verhältnis von mehr als 1:1 bedeutet, dass das Signal stärker ist als das Rauschen.
Wie berechnet man das Signal-Rausch-Verhältnis?
Das SNR wird normalerweise in Dezibel (dB) angegeben. Die Formel für das Signal-Rausch-Verhältnis lautet:
SNR=10lg(Ps/Pn)
oder
SNR=20lg(Vs/Vn)
Dabei stehen „Ps” und „Pn” für die effektive Leistung des Signals bzw. des Rauschens und „Vs” und „Vn” für die effektiven Werte der Signal- bzw. Rauschspannung.
Simulationsberechnung
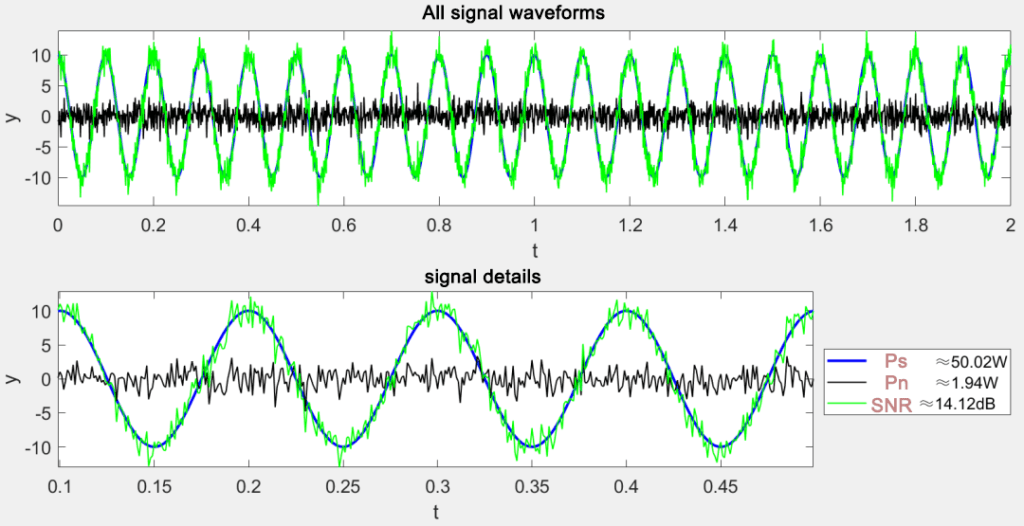
Der folgende Fall verwendet das Leistungsverhältnis als Beispiel für die Durchführung von Simulationsberechnungen:
%% Calculating the SNR Simulation
clear; clc; close all; warning off;
% parameter settings
T = 2; % Simulation time
fs = 1000; % Sampling frequency
t = 0 : 1/fs : T;
L = length(t);
A = 10; % Amplitude
fc = 10; % carrier frequency
P_n = 2; % noise power
% generate simulated signal
signal = A * cos(2 * pi * fc .* t); % generate a valid signal
noise = sqrt(P_n) .* randn(1, L); % Generate white Gaussian noise signal
% Calculating SNR
P_s = sum(signal .^ 2) / L; % signal power
P_n = sum(noise .^ 2) / L; % noise power
SNR = 10 * log10(P_s / P_n); % signal-to-noise ratio
fprintf('\t Ps:%.2fW\n', P_s);
fprintf('\t Pn:%.2fW\n', P_n);
fprintf('\t SNR:%.2fdB\n', SNR);
figure(1); clf;
subplot(2, 1, 1);
plot(t, signal, 'b', 'linewidth', 2); hold on;
plot(t, noise, 'k', 'linewidth', 1); hold on;
plot(t, signal+noise, 'g', 'linewidth', 1);
xlabel('t'); ylabel('y'); axis('tight'); title('All waveforms'); set(gca, 'fontsize', 14);
subplot(2, 1, 2);
plot(t(100:500), signal(100:500), 'b', 'linewidth', 2); hold on;
plot(t(100:500), noise(100:500), 'k', 'linewidth', 1); hold on;
plot(t(100:500), signal(100:500)+noise(100:500), 'g', 'linewidth', 1);
legend(['signal power≈', num2str(P_s, '%.2f'), 'W'], ['noise power≈', num2str(P_n, '%.2f'), 'W'], ...
['SNR≈', num2str(SNR, '%.2f'), 'dB'], 'location', 'eastoutside');
xlabel('t'); ylabel('y'); axis('tight'); title('Zoom in to observe signal details'); set(gca, 'fontsize', 14);
set(gcf, 'position', [12, 60, 1450, 650]);
Analog-Digital-Wandler Signal-Rausch-Verhältnis
ADC SNR wird verwendet, um die Qualität eines Digital-Analog-Wandlers (DAC) oder Analog-Digital-Wandlers (ADC) zu messen. Um mehr über diese wichtigen Komponenten zu erfahren, lesen Sie unseren Leitfaden zu ADC- und DAC-Wandlern: Wie sie funktionieren. Je höher der ADC-SNR-Wert, desto besser ist die Leistung des Wandlersystems. Für jedes Signalsystem ist es unerlässlich, einen guten ADC-SNR-Wert aufrechtzuerhalten, um genaue Ausgangssignale zu liefern.
ADC-SNR-Berechnung
ADC-SNR-Formel:
SNR=6,02N+1,76dB
„N” ist die Anzahl der Bits des ADC.
Formelableitung
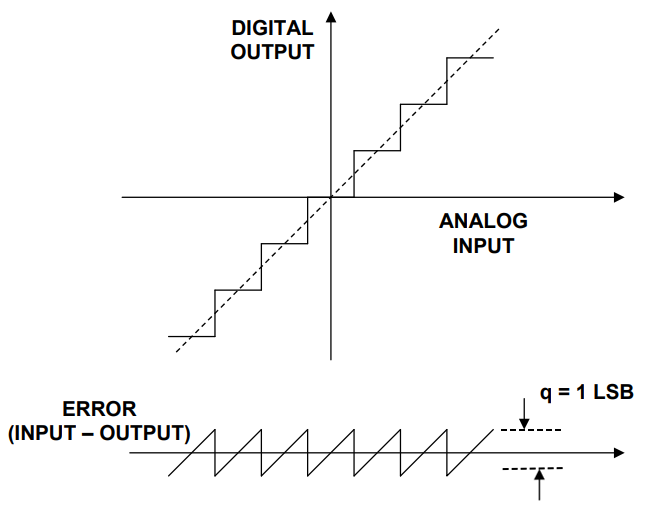
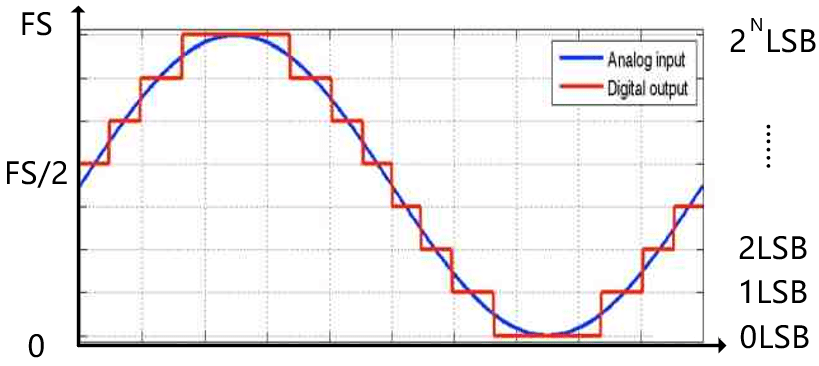
Die folgende Abbildung zeigt ein schematisches Diagramm des Quantisierungsrauschens eines idealen ADC. Wie aus der Abbildung ersichtlich ist, erzeugt der ADC bei einem linearen analogen Eingangssignal ein stufenförmiges Ausgangssignal. Die Fehlerwellenform dieses Eingangs und Ausgangs ähnelt einer Sägezahnwelle mit einem Spitze-Spitze-Wert q=1LSB. Der Berechnungsprozess für den effektiven Wert RMS ist in Formel (1) (q=1LSB) dargestellt, der Berechnungsprozess für LSB ist in Formel (2) dargestellt, wobei FS der Eingangsspannungsbereich des ADC ist.
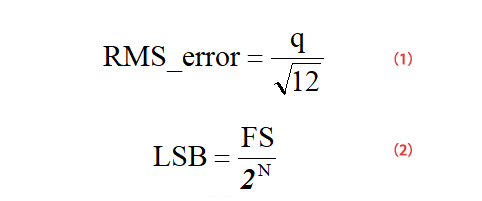
Da das Signal-Rausch-Verhältnis der Effektivwert (RMS) des Signals geteilt durch den Effektivwert (RMS) des Rauschens ist, erhalten wir die Formel (3):
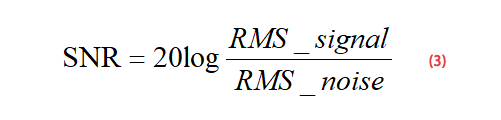
Für ein sinusförmiges Eingangssignal voller Amplitude, wie in Formel (4) dargestellt, lässt sich gemäß Formel (4) die Formel (5) ableiten:
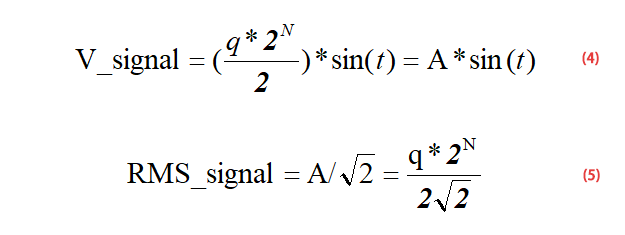
Bei einem ADC mit vollem Messbereich beträgt sein Eingangsbereich 0-FS, dann ist der Amplitudenbereich des sinusförmigen Eingangssignals 0-Fs/2, siehe das folgende schematische Diagramm, sodass der Nenner in Formel (4) 2 ist.
Bisher kennen wir den Effektivwert (RMS) des Signals – Formel (5) – und den Effektivwert (RMS) des ADC-Quantisierungsrauschens – Formel (1). Nun setzen wir Formel (5) und Formel (1) in Formel (3) ein, um Formel (6) zu erhalten:
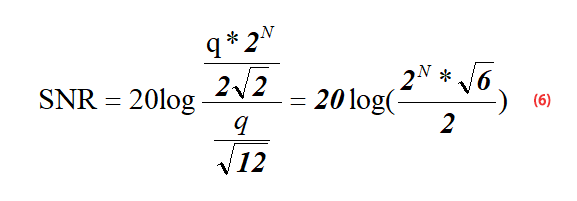
Nach Vereinfachung der Formel (6) erhalten wir die folgende Formel 7: