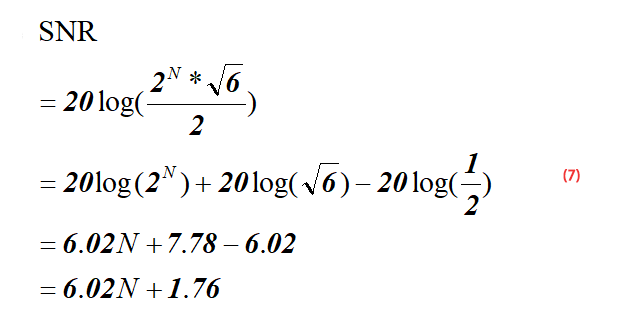Qu'est-ce que le rapport signal sur bruit ?
Le rapport signal sur bruit (SNR) est une mesure utilisée en science et en ingénierie qui compare le niveau d’un signal souhaité au niveau du bruit de fond. Il est défini comme le rapport de la puissance du signal à la puissance du bruit. Un rapport supérieur à 1:1 indique plus de signal que de bruit.
Comment calculer le rapport signal sur bruit ?
Le SNR est généralement exprimé en décibels (dB). La formule du rapport signal sur bruit est :
SNR=10lg(Ps/Pn)
ou
SNR=20lg(Vs/Vn)
Parmi eux, “Ps” et “Pn” représentent la puissance effective du signal et du bruit respectivement, et “Vs” et “Vn” sont les valeurs efficaces de la tension du signal et du bruit.
Calcul de simulation
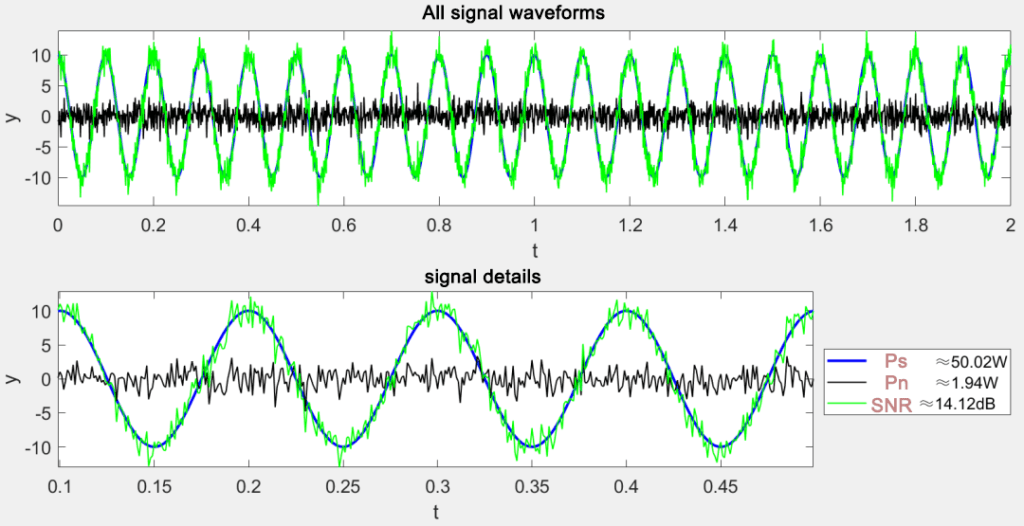
Le cas suivant utilisera le rapport de puissance comme exemple pour effectuer des calculs de simulation :
%% Calculating the SNR Simulation
clear; clc; close all; warning off;
% parameter settings
T = 2; % Simulation time
fs = 1000; % Sampling frequency
t = 0 : 1/fs : T;
L = length(t);
A = 10; % Amplitude
fc = 10; % carrier frequency
P_n = 2; % noise power
% generate simulated signal
signal = A * cos(2 * pi * fc .* t); % generate a valid signal
noise = sqrt(P_n) .* randn(1, L); % Generate white Gaussian noise signal
% Calculating SNR
P_s = sum(signal .^ 2) / L; % signal power
P_n = sum(noise .^ 2) / L; % noise power
SNR = 10 * log10(P_s / P_n); % signal-to-noise ratio
fprintf('\t Ps:%.2fW\n', P_s);
fprintf('\t Pn:%.2fW\n', P_n);
fprintf('\t SNR:%.2fdB\n', SNR);
figure(1); clf;
subplot(2, 1, 1);
plot(t, signal, 'b', 'linewidth', 2); hold on;
plot(t, noise, 'k', 'linewidth', 1); hold on;
plot(t, signal+noise, 'g', 'linewidth', 1);
xlabel('t'); ylabel('y'); axis('tight'); title('All waveforms'); set(gca, 'fontsize', 14);
subplot(2, 1, 2);
plot(t(100:500), signal(100:500), 'b', 'linewidth', 2); hold on;
plot(t(100:500), noise(100:500), 'k', 'linewidth', 1); hold on;
plot(t(100:500), signal(100:500)+noise(100:500), 'g', 'linewidth', 1);
legend(['signal power≈', num2str(P_s, '%.2f'), 'W'], ['noise power≈', num2str(P_n, '%.2f'), 'W'], ...
['SNR≈', num2str(SNR, '%.2f'), 'dB'], 'location', 'eastoutside');
xlabel('t'); ylabel('y'); axis('tight'); title('Zoom in to observe signal details'); set(gca, 'fontsize', 14);
set(gcf, 'position', [12, 60, 1450, 650]);
SNR ADC
Le rapport signal sur bruit (SNR) ADC est utilisé pour mesurer la qualité d’un convertisseur numérique-analogique (DAC) ou d’un convertisseur analogique-numérique (ADC). Pour en savoir plus sur ces composants essentiels, consultez notre guide sur Les convertisseurs ADC et DAC : comment ils fonctionnent. Plus la valeur du SNR ADC est élevée, meilleures sont les performances du système de conversion. Il est essentiel pour tout système de signal de maintenir une bonne valeur de SNR ADC afin de fournir des signaux de sortie précis.
Calcul du SNR ADC
formule du SNR ADC :
SNR=6.02N+1.76dB
« N » est le nombre de bits de l’ADC.
Dérivation de la formule
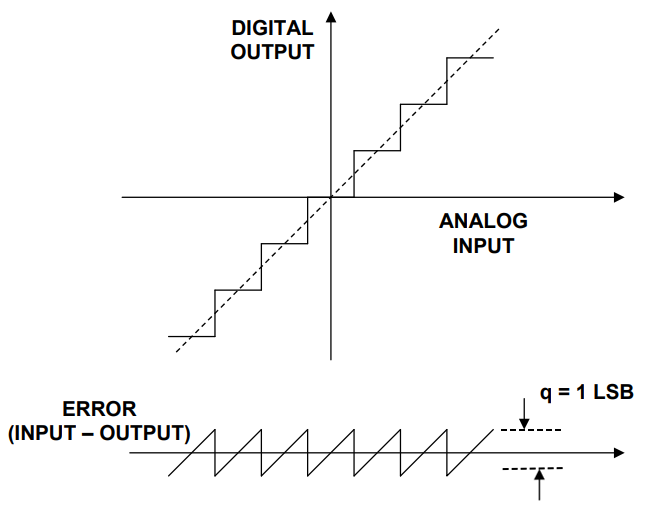
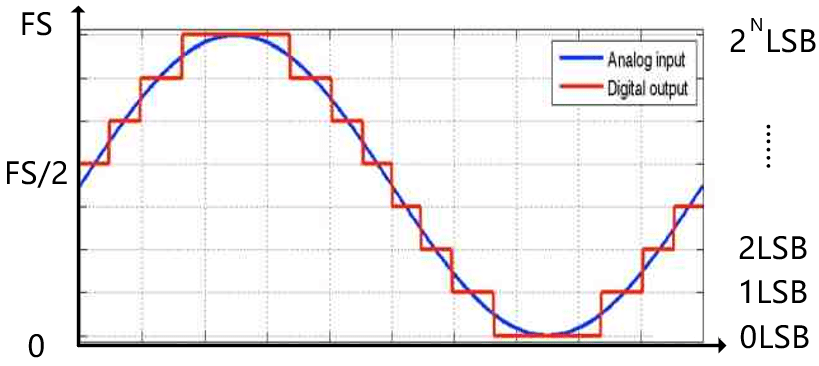
La figure ci-dessous est un schéma du bruit de quantification d’un ADC idéal. Comme on peut le voir sur la figure ci-dessous, pour un signal analogique d’entrée linéaire, l’ADC produira une sortie échelonnée. La forme d’onde d’erreur de cette entrée et de cette sortie est similaire à une dent de scie avec une valeur crête à crête q=1LSB, son processus de calcul de la valeur efficace RMS est présenté dans la formule (1) (q=1LSB), le processus de calcul de LSB est présenté dans la formule (2), où FS est la plage de tension d’entrée de l’ADC.
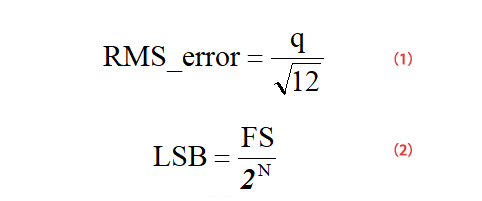
Puisque le rapport signal sur bruit est la valeur efficace (RMS) du signal divisée par la valeur efficace (RMS) du bruit, nous pouvons obtenir la formule (3) :
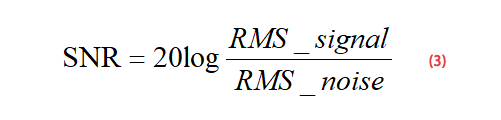
Pour un signal sinusoïdal d’entrée à pleine échelle comme indiqué dans la formule (4), la formule (5) peut être obtenue selon la formule (4) :
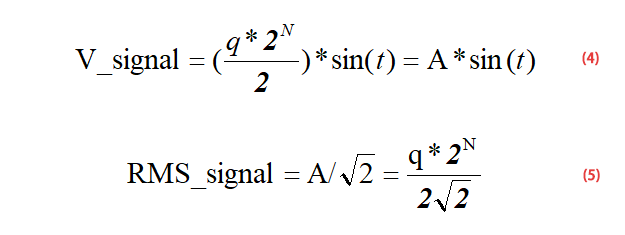
Pour un ADC à pleine échelle, sa plage d’entrée est de 0 à FS, alors la plage d’amplitude du signal sinusoïdal d’entrée est de 0 à Fs/2, voir le schéma ci-dessous, donc le dénominateur dans la formule (4) est 2.
Jusqu’à présent, nous connaissons la valeur efficace (RMS) du signal – formule (5), et la valeur efficace (RMS) du bruit de quantification du CAN – formule (1). Maintenant, nous introduisons la formule (5) et la formule (1) dans la formule (3) pour obtenir la formule (6) :
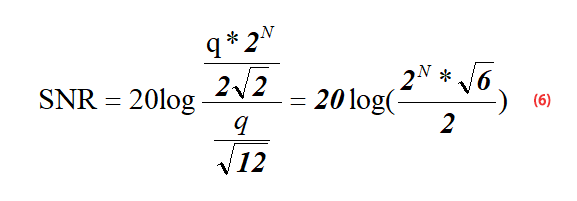
Après simplification de la formule (6), nous pouvons obtenir la formule 7 ci-dessous :