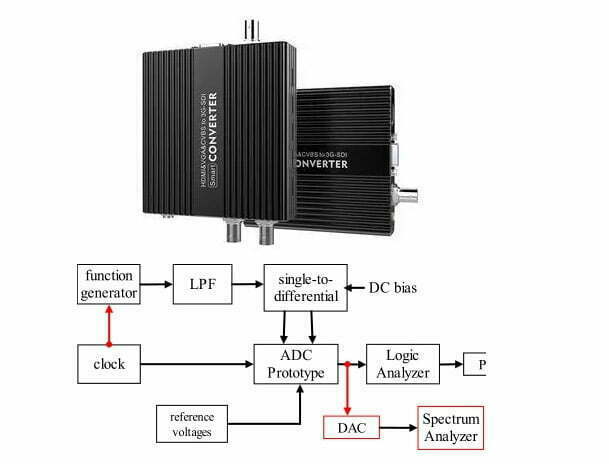
Entre os instrumentos inteligentes, os conversores ADC e DAC desempenham um papel fundamental. Sabemos que os microprocessadores amplamente utilizados atualmente só conseguem lidar com sinais digitais discretos. Não há como alimentar um sinal analógico contínuo do mundo físico em um microprocessador sem um ADC. Além disso, sem um DAC, não há como emitir um sinal analógico a partir de um microprocessador. (clique aqui para saber mais sobre sinal digital e sinal analógico)
Conversor analógico-digital (ADC)
Definição de ADC
No sistema de instrumentação, muitas vezes é necessário converter as grandezas analógicas detectadas em constante mudança, como temperatura, pressão, vazão, velocidade, intensidade luminosa, etc., em grandezas digitais discretas antes de inseri-las no computador para processamento. Essas grandezas analógicas são convertidas em sinais elétricos (geralmente sinais de tensão) por sensores e, após serem amplificadas por amplificadores, precisam passar por um determinado processamento para se tornarem grandezas digitais. Um dispositivo que converte analógico em digital é geralmente chamado de conversor analógico-digital (ADC) ou A/D, para abreviar.
Princípio de funcionamento do ADC
Em circunstâncias normais, a conversão A/D geralmente precisa passar por quatro processos: amostragem, retenção, quantização e codificação.
Amostragem e retenção
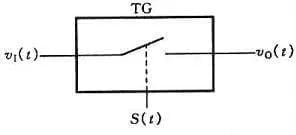
A amostragem consiste em converter uma quantidade analógica que muda continuamente com o tempo numa quantidade analógica discreta no tempo. O diagrama esquemático do processo de amostragem é apresentado na Figura 1. A Figura (a) é uma estrutura de circuito de amostragem, na qual a porta de transmissão é controlada pelo sinal de amostragem S(t). Durante a largura de pulso τ de S(t), a porta de transmissão é ativada, o sinal de saída vO(t) é o sinal de entrada v1 e, durante (Ts-τ), a porta de transmissão é fechada e o sinal de saída vO(t)=0. As formas de onda do sinal no circuito são mostradas na Figura (b).
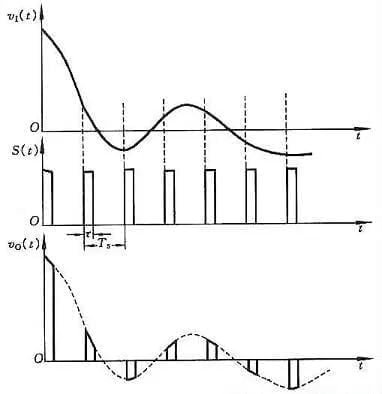
A partir da análise, pode-se observar que quanto maior a frequência do sinal de amostragem S(t), mais fielmente o sinal obtido pode reproduzir o sinal de entrada após passar pelo filtro passa-baixa. Mas o problema é que a quantidade de dados aumenta. Para garantir uma frequência de amostragem adequada, ela deve satisfazer o teorema da amostragem.
Teorema de amostragem: Suponha que a frequência do sinal de amostragem S(t) seja fs e que a frequência do componente de frequência mais alta do sinal analógico de entrada v1(t) seja fimax. Então, fs e fimax devem satisfazer a seguinte relação: fs≥2fimax, e fs> é geralmente considerado em engenharia (3~5) fimax.
Leva um certo tempo para converter o sinal analógico obtido pelo circuito de amostragem em um sinal digital a cada vez. Para fornecer um valor estável para o processo subsequente de quantização e codificação, o sinal analógico obtido a cada vez deve ser mantido por um período de tempo pelo circuito de retenção.
O processo de amostragem e retenção é frequentemente concluído simultaneamente através do circuito de amostragem-retenção. O diagrama esquemático e a forma de onda de saída do circuito de amostragem-retenção são mostrados na Figura 2.
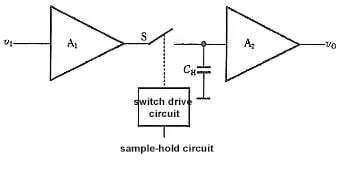
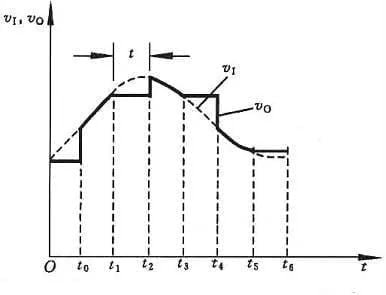
O circuito é composto por um amplificador de entrada A1, um amplificador de saída A2, um capacitor de retenção CH e um circuito de acionamento do interruptor. O A1 deve ter uma alta impedância de entrada no circuito para reduzir a influência na fonte do sinal de entrada. Para dificultar a descarga da carga armazenada no CH durante a fase de retenção, o A2 também deve ter uma alta impedância de entrada e uma baixa impedância de saída, o que pode melhorar a capacidade de carga do circuito. Geralmente, também é necessário que AV1·AV2=1 no circuito.
Agora, em conjunto com a Figura 2, analise a amostra – mantenha o princípio de funcionamento do circuito. Em t=t0, o interruptor S é fechado e o capacitor é carregado rapidamente. Como AV1 · AV2=1, v0=vI, o período de amostragem é durante o intervalo de tempo de t0~t1. No momento t=t1, S é desconectado. Se a impedância de entrada de A2 for infinita e S for um interruptor ideal, pode-se considerar que o capacitor CH não tem circuito de descarga e que a tensão em ambas as extremidades permanece constante em v0. A seção plana de t1 a t2 na Figura 11.8.2(b) é o estágio de retenção.
O circuito de amostragem e retenção pode ser produzido por vários tipos de circuitos integrados monolíticos. Por exemplo, existem AD585 e AD684 para tecnologia bipolar; AD1154 e SHC76 para tecnologia mista.
Quantização e codificação
Os sinais digitais não são apenas discretos no tempo, mas também descontínuos em amplitude. O tamanho de qualquer quantidade digital só pode ser um múltiplo inteiro de uma unidade de quantidade mínima especificada. Para converter o sinal analógico em uma quantidade digital, no processo de conversão A/D, a tensão de saída do circuito de amostragem e retenção também deve ser normalizada para o nível discreto correspondente de uma determinada maneira aproximada. Esse processo de conversão é chamado de valor numérico. Quantificação, referida como quantificação. O valor quantizado precisa finalmente ser representado por um código através do processo de codificação. O código obtido após a codificação é a quantidade digital emitida pelo conversor A/D.
A menor unidade de quantidade considerada no processo de quantização é chamada de unidade de quantização, representada por △. É a quantidade analógica correspondente a quando o bit mais baixo do sinal digital é 1, ou seja, 1LSB.
No processo de quantização, como a tensão de amostragem não é necessariamente divisível por △, há inevitavelmente um erro antes e depois da quantização. Esse erro é chamado de erro de quantização e é representado por ε. O erro de quantização é um erro de princípio, que não pode ser eliminado. Quanto mais bits o conversor A/D tiver, menor será a diferença entre os níveis discretos e menor será o erro de quantização.
Dois métodos de quantização aproximada são frequentemente usados no processo de quantização: apenas quantização de arredondamento e quantização de arredondamento.
apenas arredondando o método de quantização
Tomando como exemplo o conversor A/D de 3 bits, deixe o sinal de entrada v1 variar de 0 a 8 V. Ao usar o método de quantização arredondada, considere △=1 V e descarte a parte que não é suficiente na unidade de quantização. Se o valor estiver entre 0 e 8 V, a tensão analógica entre 1 V é considerada como 0△, representada pelo número binário 000, e a tensão analógica entre 1 V e 2 V é considerada como 1△, representada pelo número binário 001… O erro máximo desse método de quantização é △.
método de quantização de arredondamento
Se for adotado o método de quantização por arredondamento, será utilizada a unidade de quantização △=8V/15, e a parte inferior a metade da unidade de quantização será descartada durante o processo de quantização, enquanto a parte igual ou superior a metade da unidade de quantização será tratada como uma unidade de quantização. Ele trata a tensão analógica entre 0 ~ 8V/15 como 0△, representada pelo binário 000, e a tensão analógica entre 8V/15 ~ 24V/15 é considerada como 1△, representada pelo número binário 001, que significa espera.
Comparação
O erro máximo de quantização│εmax│=1LSB no método de quantização anterior com apenas arredondamento, e o método de quantização│εmax│=1LSB/2 no método de quantização posterior com arredondamento e arredondamento, o erro de quantização do último é menor do que o do primeiro, por isso é o conversor A/D mais utilizado.
Com o rápido desenvolvimento dos circuitos integrados, novas ideias de design e técnicas de fabricação para conversores A/D surgem em um fluxo interminável. Conversores A/D com diferentes estruturas e desempenhos são projetados para atender a várias necessidades de detecção e controle.
Tipos de ADC
Integração do ADC
princípio de conversão
O princípio de conversão da integração do ADC baseia-se na integração da tensão e na comparação da tensão integrada com outra tensão para controlar a contagem, sendo que a saída da contagem é a saída do ADC. O objeto da integração baseia-se na tensão de referência ou na tensão de referência e na tensão de entrada.
Prós e contras
Vantagens:
- O ADC integral tem alta resolução, e o número de dígitos pode ser 12 ou até mais.
- A linearidade é muito boa. Essencialmente, a entrada é comparada com uma tensão de referência integrada para determinar a saída, portanto, a linearidade dependerá da precisão do comparador.
- A topologia de realização do circuito é simples e há relativamente poucos componentes usados para realizar esses dispositivos, portanto, o circuito é relativamente simples e o custo de produção é baixo.
Desvantagem:
- A principal desvantagem é a baixa velocidade de conversão. No ADC de N bits, a saída pode levar até 2 N ciclos de clock para converter um único ponto de amostra.
Aplicações
Utilizado principalmente em aplicações e dispositivos sensores, tais como voltímetros e amperímetros, onde a precisão é mais importante do que a velocidade. Por outras palavras, a velocidade de amostragem do ADC integral é relativamente baixa, mas a precisão é muito elevada.
classificação
Existem diferentes tipos de ADCs integrais, sendo os mais comuns os integrais de inclinação simples e dupla. Adicionar uma "inclinação" aumenta a precisão, mas aumenta o tempo de conversão.
ADC integral de inclinação única
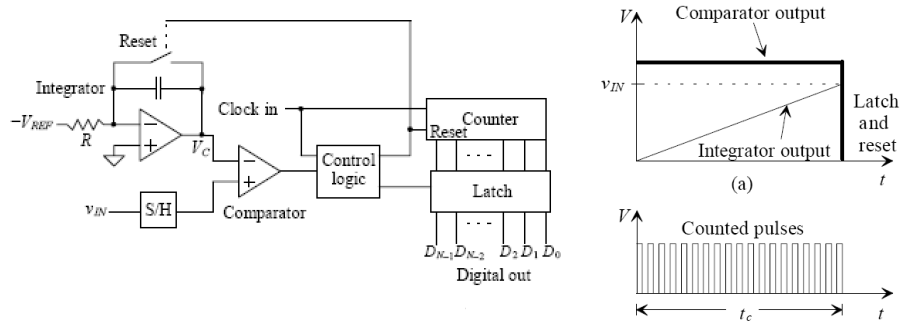
O comparador compara a tensão de entrada com o valor da tensão de referência integrada (note que vamos torná-la negativa, uma vez que está ligada à entrada inversora do amplificador operacional). Conta simultaneamente o número de ciclos de relógio. Quando a saída do integrador é igual, o comparador emite um "0" lógico, desencadeando uma reinicialização do contador e do integrador, e o latch mantém a saída digital.
VINVREFVrefVrefVin
Este é o tempo de conversão. Eu sei por que este ADC integral é lento. Vamos examinar o pior caso, assumindo a tensão de entrada , assumindo , assumindo que é um ADC de 20 bits, então!
VIN=VREFTCLK=1ustc=220us=1048576us
ADC integral de inclinação única
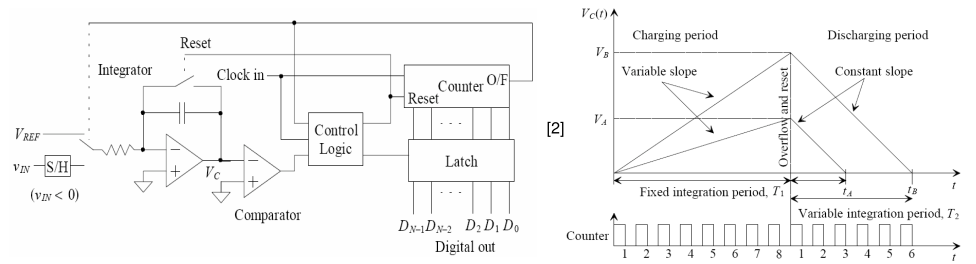
Um ADC de dupla inclinação difere de um ADC de inclinação única, pois a comparação com o terra é agora feita e duas somas de tensões são integradas. Inicialmente, a entrada negativa é conectada ao integrador, que aumenta até o contador transbordar. Como a integração na entrada inversora muda para um valor negativo, a saída do integrador será sempre positiva e maior que zero, de modo que o contador continuará funcionando até transbordar, o que leva 2N ciclos de clock (=T1).
VCVREFVINVC
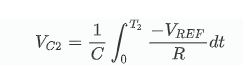
No tempo T2, será igual à soma de e, e
VC=VC1+VC2=0
Mas:
VIN/VREF=T2/T1
Portanto, pelo princípio da conversão ADC, o ADC de dupla inclinação é mais lento que o ADC de inclinação única, já que a integração é feita duas vezes, o erro relacionado à inclinação do integrador vai ser cancelado, melhorando assim a precisão em princípio.
ADC Sigma-Delta Σ-Δ
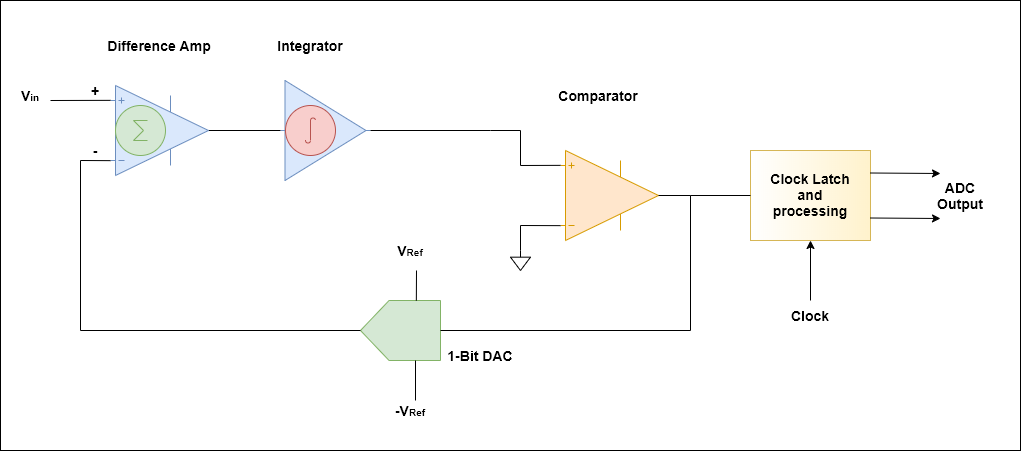
Começando na entrada, o amplificador diferencial produz uma saída que é a diferença entre Vin e a saída DAC de 1 bit. A saída de um DAC de 1 bit pode ser um dos dois valores: OR . Nesta topologia, um integrador pode ser considerado como tomando uma média móvel do valor anterior e do valor de entrada atual.
–Vref+Vref
Portanto, supondo que o segmento positivo do comparador esteja inicialmente fixado em um pequeno valor acima de 0 V, o comparador se inverte. Seu valor será alto ou 1. Então, a saída do DAC será . Na próxima iteração, esse valor será subtraído do valor atual de . Como o valor anterior era 0 V, a saída do integrador agora será – Vref. Nesse ponto, a saída do comparador será 0 e a saída do DAC será.
+VrefVin-Vref
Na próxima amostra , a saída do integrador será 0 devido ao valor anterior, e o amplificador diferencial irá subtrair , adicionando assim a . A saída do comparador será 1.
-Vref-Vref+VrefVin
Esse processo continua iterativamente, portanto, para uma entrada de 0 V, a saída do comparador será um fluxo constante de 101010…. Lembre-se de que a lógica 1 significa , a lógica 0 significa , portanto, se N amostras forem amostradas e calculadas, é fácil ver que o valor médio é 0 V. O bloco de processamento após o comparador simplesmente emitirá isso como um único valor 0000…, assumindo um valor de referência de ( ~ ) ou 2 x.
+Vref-Vref-Vref+VrefVref
Agora, assumindo 1 V, este é um ADC de 5 V. é ±2,5 V. Seguindo os mesmos passos de antes iterativamente, a saída será: 1011101… A saída é 1,07 V.
Vin±Vref
Em resumo:
Um ADC sigma-delta sobreamostra o sinal que está sendo processado (consulte Como funciona a amostragem analógica-digital para entender esse conceito) e aplica um filtro passa-baixa ao sinal a ser processado. Normalmente, o número de bits convertidos usando o ADC Flash após o filtro é menor do que o número de bits necessário. O sinal resultante, juntamente com os erros dos níveis discretos FLASH, é realimentado e subtraído da entrada e enviado ao filtro. Esse feedback negativo amortece o ruído para que ele não apareça na frequência de sinal desejada. Um filtro digital após o ADC (usando um filtro de decimação) reduz a taxa de amostragem, filtra sinais de ruído indesejados e aumenta a resolução de saída (daí o nome modulação sigma-delta, também conhecida como modulação delta-sigma).
ADC Flash (tipo de comparação direta)
O princípio do FLASH ADC pode ser o mais fácil de entender. A figura abaixo é um diagrama esquemático de um ADC de dois bits, que consiste em muitos comparadores, cada um dos quais é fornecido com uma tensão de referência que é um bit mais alta do que o valor de referência anterior. Portanto, para um ADC de 8 bits, são necessários 256 desses comparadores. Para 10 bits, são necessários 1024.
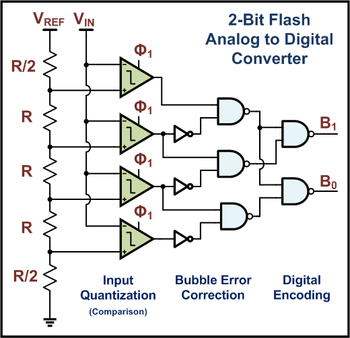
O LASH ADC (tipo de comparação direta) é rápido. Ele converte diretamente a entrada sem qualquer amostragem ou pós-processamento pesado. O problema é que ele requer muitos comparadores, e muitos comparadores ocupam muito espaço de silício no chip. Portanto, use ADCs Fash apenas quando precisar de velocidades extremamente altas que não podem ser alcançadas com outras implementações de ADC.
Dicotomia incorporada no hardware
Em aplicações práticas, existe outra variante mais comumente usada, o ADC semi-FLASH. Ele usa um processo de duas etapas para reduzir o número de conversores necessários na cadeia de conversão real:
Primeiro, o sinal de entrada é comparado com o conjunto de níveis que se encontram exatamente na metade . Se for inferior, o bit mais significativo, MSB, é definido como 0 e a entrada é alimentada a uma cadeia de comparadores com a tensão de referência definida para converter o resto dos bits.
Se o sinal de entrada estiver acima, defina o MSB como 1 e subtraia do sinal de entrada. A cadeia de comparadores é usada novamente para obter os bits restantes. Portanto, em essência, o ADC FLASH de meio passo sacrifica uma comparação extra para economizar metade do comparador. Esse tipo de raciocínio também pode continuar a ser deduzido e expandido, como o ADC FLASH de 4 pontos e assim por diante.
O registro de aproximação sucessiva (SAR)
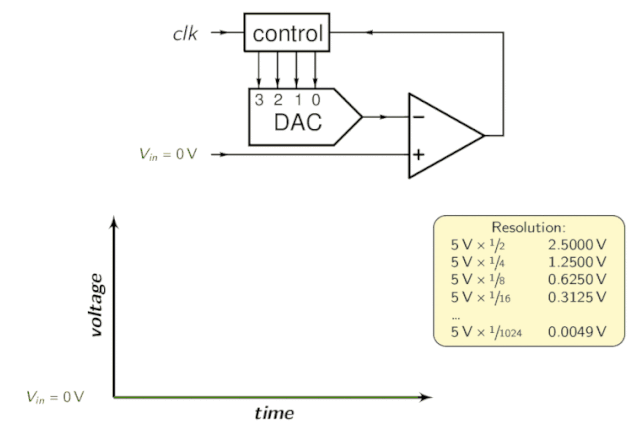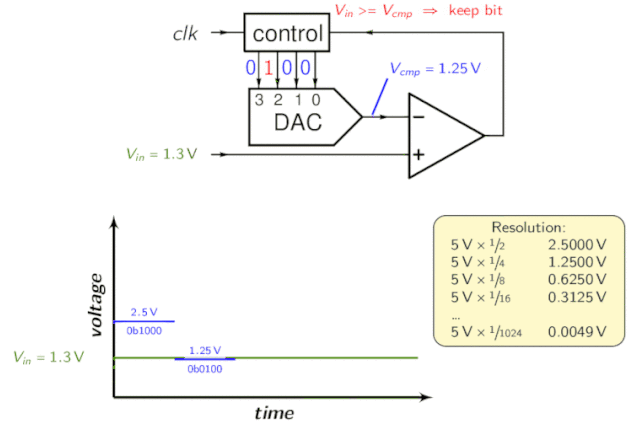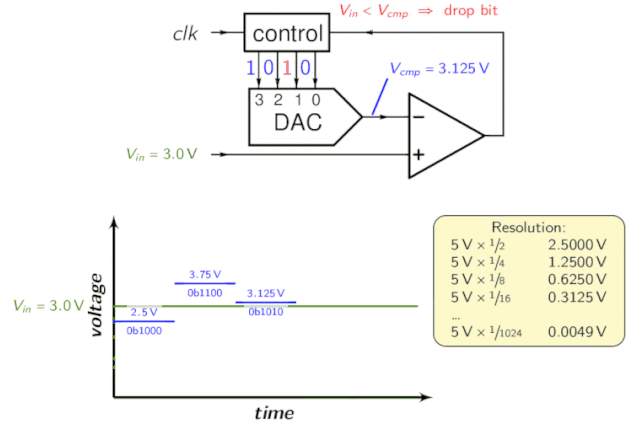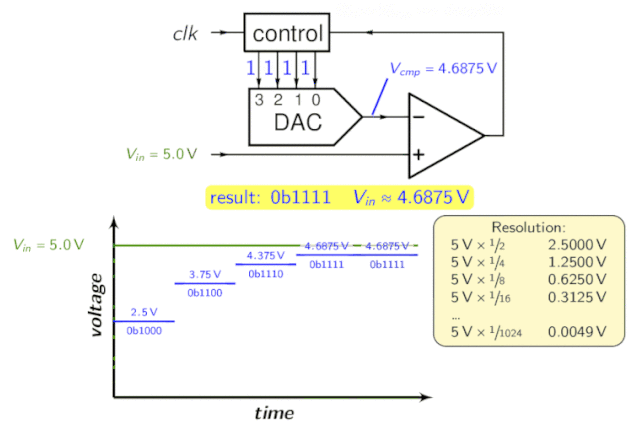
O Registro de Aproximação Sucessiva (SAR) é parte integrante do ADC de aproximação sucessiva. Ele funciona utilizando um comparador para reduzir gradualmente a área que contém a tensão de entrada. Para fazer isso, o conversor compara a tensão de entrada com a saída de um conversor digital-analógico, que geralmente indica o meio da faixa de tensão escolhida. A cada etapa do processo, a estimativa é armazenada no SAR.
Por exemplo, suponha que a tensão de entrada seja 6,3 V e a faixa inicial seja de 0 a 16 V.
- Na primeira etapa, insira 6,3 V para comparar com 8 V (o ponto médio da faixa de 0 a 16 V). O comparador relata uma tensão de entrada inferior a 8 V, então o SAR é atualizado para reduzir a faixa para 0 a 8 V.
- Na segunda etapa, a tensão de entrada é comparada a 4 V (o ponto médio de 0 a 8 V), o comparador relata que a tensão de entrada está acima de 4 V, então o SAR é atualizado para refletir que a tensão de entrada está na faixa de 4 a 8 V.
- Na terceira etapa, a tensão de entrada é comparada a 6 V (metade de 4 V a 8 V); o comparador relata uma tensão de entrada superior a 6 volts, e a faixa de pesquisa passa a ser de 6 a 8 volts.
Continue essas etapas até chegar à solução desejada. Sua topologia é a seguinte:
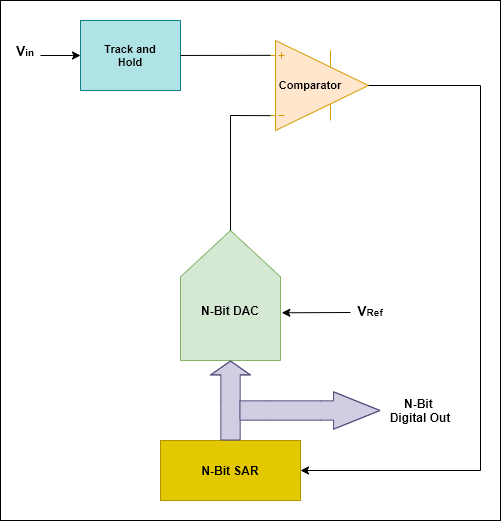
Para entender melhor, veja a animação a seguir:
ADC em pipeline
Um ADC em pipeline (também conhecido como quantizador de sub-rotina) usa dois ou mais pipelines. Primeiro, faça uma conversão aproximada. Na segunda etapa, um conversor digital-analógico (DAC) é usado para determinar a diferença no sinal de entrada. Essa diferença é então convertida em valores mais precisos e os resultados são combinados em uma etapa final. Isso pode ser considerado uma melhoria em relação aos ADCs de aproximação sucessiva, nos quais o sinal de referência de feedback consiste em transições intermediárias em toda a faixa de bits (por exemplo, 4 bits), em vez de apenas o próximo bit mais significativo. Combinando as vantagens do método de aproximação sucessiva e do ADC flash, esse tipo tem as vantagens de alta velocidade, alta resolução e tamanho de molde pequeno.
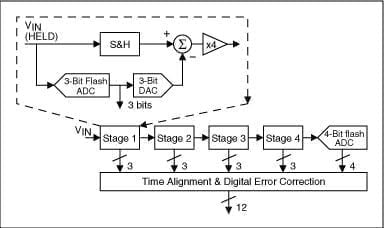
Neste esquema, a entrada analógica VIN é primeiro amostrada e mantida estável por um amostrador e retentor (S&H), enquanto o ADC flash no primeiro estágio a quantiza para três bits. A saída de 3 bits é então enviada para um DAC de 3 bits (precisão de 12 bits) e a saída analógica é subtraída da entrada. Esse "restante" é ampliado por um fator de 4 e enviado para o próximo estágio (estágio 2). Esse restante adicionado continua pelos estágios inferiores do pipeline, fornecendo 3 bits por estágio, até chegar ao ADC flash de 4 bits, que resolverá os 4 bits 4LSB finais. Como os bits para cada estágio são determinados em momentos diferentes, todos os bits correspondentes à mesma amostra são alinhados no tempo com o registro de deslocamento antes de serem enviados para a lógica de correção de erros digitais. Observe que, quando um pipeline termina de processar as amostras de entrada, determina o bit de aquisição para esse pipeline e passa o resíduo para o próximo pipeline, ele pode começar a processar a próxima amostra recebida do suporte de amostras incorporado em cada pipeline. Esse pipeline é a razão para o alto rendimento, que também é o conceito de pipeline.
Outros
Além dos vários ADCs comuns acima mencionados, existem também ADCs com princípio de equilíbrio de carga, ADCs com partilha de tempo, ADCs FM, ADCs com alongamento de tempo, ADCs com codificação incremental, ADCs Wilkinson, etc.
Conversor digital-analógico (DAC)
Definição de DAC
A quantidade digital processada pelo sistema digital às vezes precisa ser convertida em uma quantidade analógica para uso prático. Essa conversão é chamada de "conversão digital-analógica". O circuito que realiza a conversão digital-analógica é chamado de conversor digital-analógico, ou DAC (Digital to Analog Converter) para abreviar.
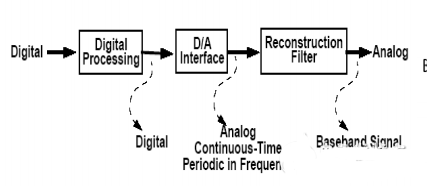
Parâmetros DAC
Resolução
A resolução no DAC é definida como o número de todos os níveis analógicos de saída possíveis sob diferentes valores de código digital de entrada. A resolução de N bits significa que o DAC pode gerar 2 N −1 níveis analógicos diferentes. Geralmente, refere-se ao número de dígitos do código digital de entrada.
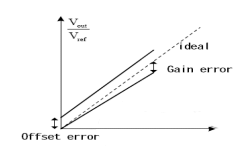
Erros de desvio e ganho
O desvio é definido como o valor do sinal analógico de saída real quando um valor de código 0 é inserido, e o erro de ganho é definido como a diferença entre o valor de saída ideal em escala total e o valor de saída real após deduzir o desvio, conforme mostrado na figura.
Precisão
A precisão no DAC é dividida em precisão absoluta e precisão relativa. A precisão absoluta é definida como a diferença entre a saída ideal e a saída real, incluindo vários erros de desvio e não lineares. A precisão relativa é definida como o erro não linear integral máximo. A precisão é expressa como uma razão da escala total, expressa em dígitos efetivos. Por exemplo, precisão de 8 bits significa que o erro do DAC é inferior a 1/8 2 da saída em escala total do DAC. Observe que o conceito de precisão não está relacionado à resolução. Um DAC com resolução de 12 bits pode ter apenas precisão de 10 bits; e um DAC com resolução de 10 bits pode ter precisão de 12 bits. Precisão sobre resolução significa que a resposta de transmissão do DAC pode ser controlada com mais precisão.
INL - Não linearidade integral
Quando os erros de desvio e ganho são removidos, o erro de linearidade integral é definido como o desvio da característica de transferência de saída real em relação à característica de transferência ideal (uma linha reta), conforme mostra a imagem.
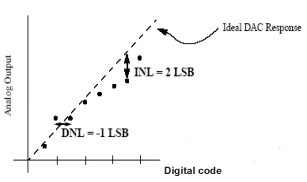
DNL - Não linearidade diferencial
Em um DAC ideal com um mínimo de 1 LSB por alteração na saída analógica, o erro de linearidade diferencial é definido como o desvio de 1 LSB por alteração mínima na saída analógica (excluindo erro de ganho e desvio). O DNL que definimos é para cada valor de código de entrada digital e, às vezes, o maior DNL é usado para definir o DNL de todo o DAC. Um DAC ideal teria erro de linearidade diferencial zero para cada entrada digital, enquanto um DAC com um DNL máximo de 0,5 LSB teria uma alteração mínima de saída entre 0,5 LSB e 1,5 LSB por saída. Os erros de linearidade integral e diferencial do DAC são mostrados na figura.
Energia de instabilidade (área de impulso de falha)
A área máxima sob o jitter que aparece na saída após a alteração do sinal de entrada.
Tempo de estabilização
O tempo de estabilização está dentro de uma faixa de erro específica do valor final e é o tempo necessário para que a saída passe por uma conversão em escala total.
Monotonicidade Um DAC monotônico é aquele em que o nível analógico de saída sempre aumenta à medida que o valor do código digital de entrada aumenta. Se o DNL máximo for controlado dentro de 0,5 LSB, a monotonicidade do DAC pode ser garantida naturalmente.
Faixa dinâmica espúria (SFDR) SFDR é a faixa dinâmica livre de espúrias, ou seja, a faixa dinâmica sem ruído e harmônicos. Tanto o ruído quanto os harmônicos são chamados de sinais espúrios.
Princípio do DAC
Converta cada código binário de entrada em uma quantidade analógica correspondente de acordo com seu peso e, em seguida, some as quantidades analógicas que representam cada bit. A quantidade analógica total obtida é proporcional à quantidade digital, realizando assim a conversão de quantidade digital para quantidade analógica. Conversão analógica.
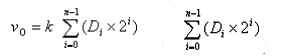
É o valor decimal convertido em um número binário por expansão do peso do bit.
Composição e características do DAC
O DAC é composto principalmente por registros digitais, interruptores eletrônicos analógicos, rede de peso de bits, amplificador operacional somador e fonte de tensão de referência (ou fonte de corrente constante). Use os dígitos das quantidades digitais armazenadas no registro digital para controlar os interruptores eletrônicos analógicos dos dígitos correspondentes, respectivamente, de modo que o dígito com um dígito 1 gere um valor de corrente proporcional ao seu peso de dígito na rede de peso de dígito e, em seguida, o amplificador operacional controle cada valor de corrente somado e convertido em um valor de tensão.
Redes de peso de bits variáveis permitem a montagem de vários tipos de DACs, incluindo o DAC de rede de resistência ponderada, o DAC de rede de resistência em forma de T invertido R-2R e o DAC de rede do tipo corrente de valor único, etc. A precisão da conversão produzida pelo DAC de rede de resistores ponderados depende da precisão da tensão de referência VREF, bem como da qualidade dos interruptores eletrônicos analógicos, amplificadores operacionais e valores de resistores ponderados. Sua desvantagem é que os valores de resistência de cada resistor de peso são diferentes e, quando há muitos dígitos, os valores de resistência variam muito, o que traz grandes dificuldades para garantir a precisão, especialmente para a produção de circuitos integrados. Portanto, no DAC integrado, esse circuito raramente é usado sozinho.
Principais indicadores técnicos do DAC
Precisão e velocidade de conversão do DAC: A precisão da conversão é geralmente descrita pela resolução e pelo erro de conversão no DAC.
Resolução
Geralmente, o número de bits do DAC é usado para medir a resolução, porque quanto maior o número de bits, mais valores (2n) da tensão de saída vO e mais ele pode refletir as mudanças sutis da tensão de saída. quanto maior.
Além disso, a resolução também pode ser definida pela relação entre a tensão de saída mínima 1 LSB que o DAC pode distinguir e a tensão de saída máxima FSR. que é:
resolução=1LSB/FSR=k/k(2n-1)=1/(2n-1)
Quanto menor o valor, maior a resolução.
Erro de conversão
O erro de conversão é o desvio máximo entre a tensão analógica de saída real e o valor ideal. Normalmente expresso como uma porcentagem ou vários LSBs da relação entre esse desvio máximo e o FSR. Na verdade, é um indicador abrangente dos três erros.
Velocidade de conversão
A velocidade de conversão é geralmente determinada pelo tempo de estabilização. Desde o momento em que a entrada muda de todos os 0s para todos os 1s, até que a tensão de saída se estabilize dentro da faixa de FSR±½ LSB (ou a faixa especificada por FSR±x%FSR), esse período é chamado de tempo de estabilização, que é a resposta máxima do DAC Time, portanto, use-o para medir a velocidade de conversão.
Tipos de DAC
Tipo de resistência
A estrutura é mostrada na Figura 1. O que a Fig. 1 mostra é um conversor do tipo rede em escada R-2R. Sua vantagem é que ele pode alcançar uma linearidade muito boa. Como todas as fontes de corrente são equivalentes, podemos usar tecnologia adicional especial para diminuir o erro entre elas, e sua estrutura é muito mais simples do que a do divisor de resistência. A desvantagem é que a resistência é sempre não linear e também contém capacitância parasítica relacionada ao sinal, por isso é difícil obter uma correspondência completa. Ao mesmo tempo, a velocidade é limitada pelo buffer de saída e não pode ser muito alta.
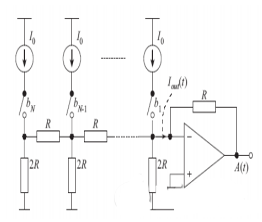
Tipo capacitivo
A estrutura é mostrada na Figura 2. A capacitância de ordem mais alta CN é 1 2N− vezes maior que a capacitância de ordem mais baixa C1. A vantagem é que o consumo de energia é pequeno e a precisão de correspondência é maior do que a do resistor. Os principais fatores limitantes são a incompatibilidade dos capacitores, a resistência dos interruptores, grandes atrasos RC e o impacto da largura de banda limitada do amplificador na velocidade do DAC. Uma grande desvantagem dos DACs de distribuição de carga é que os capacitores nos processos CMOS ocupam muita área do chip para serem implementados. Finalmente, como a capacitância no processo CMOS é de natureza não linear, a linearidade do DAC geral será suprimida. Adequado para alta precisão de banda média e larga.
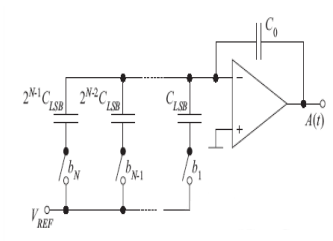
Tipo atual
A estrutura é mostrada na Figura 3. A vantagem é que, quando a precisão é inferior a 10 bits, a área pode ser muito pequena e a velocidade não é limitada pela largura de banda do amplificador e pelo grande atraso RC. Pode atingir uma velocidade muito alta. Como toda a corrente flui diretamente para o terminal de saída, o consumo de energia é altamente eficiente e fácil de implementar. As desvantagens são a sensibilidade à incompatibilidade do dispositivo e a impedância de saída limitada da fonte de corrente. Adequado para requisitos de banda larga de alta velocidade.
Também é possível não usar um amplificador operacional para saída e usar diretamente a resistência de carga para converter a corrente em uma saída de tensão, conforme mostrado na Figura 4. Essa forma permite que a taxa do DAC não seja limitada pela largura de banda do amplificador operacional.
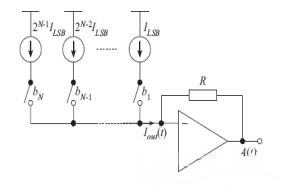
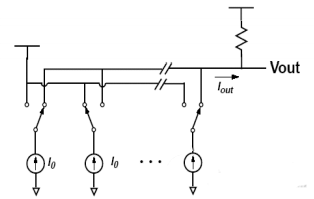
Multiplicação típica
Alguns dos conversores DA utilizam uma tensão de referência constante e outros adicionam um sinal CA à entrada da tensão de referência. Estes últimos são denominados conversores DA do tipo multiplicador, pois podem obter o resultado da multiplicação entre a entrada digital e a entrada da tensão de referência. Em geral, um conversor DA multiplicador não só pode realizar multiplicações, como também pode ser utilizado como atenuador para atenuar digitalmente um sinal de entrada e como modulador para modular um sinal de entrada.
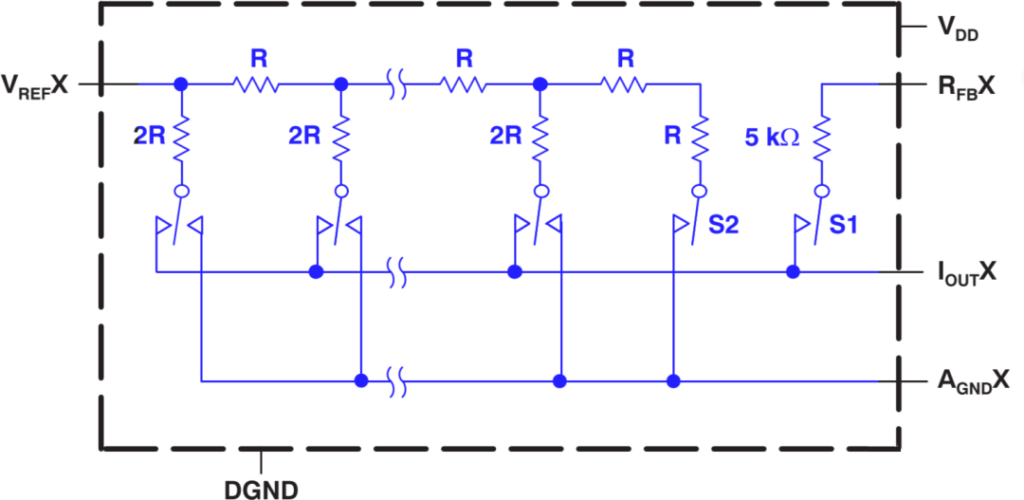
One DA converter
Ao contrário do sistema de conversão acabado de referir, um conversor DA utiliza um método especial para transformar valores digitais numa modulação por largura de impulso ou modulação por frequência, que é depois suavizada com um filtro digital para produzir uma saída de tensão comummente utilizada (também conhecida como modo de fluxo de bits) para áudio, etc.
Conclusão
Os conversores ADC e DAC são dois componentes essenciais de qualquer sistema digital. Eles ajudam a converter sinais analógicos em sinais digitais e vice-versa. O ADC (conversor analógico-digital) recebe um sinal analógico e o converte em um sinal digital, enquanto o DAC (conversor digital-analógico) recebe um sinal digital e o converte em um sinal analógico. Ambos os componentes são importantes para uma ampla gama de aplicações, desde processamento de áudio e vídeo até transmissão de dados. Neste artigo, discutimos como esses conversores funcionam e sua importância em diferentes aplicações. Também exploramos os diferentes tipos de conversores, os diferentes tipos de sinais que eles podem converter e as vantagens e desvantagens de cada tipo.