Radio Horizon Calculator
Accurately calculate radio signal propagation distance considering antenna height and Earth's curvature. Essential for amateur radio, broadcasting, and maritime communication.
Radio Horizon Calculator
Enter antenna height to calculate the theoretical propagation distance of radio signals. Supports single and dual antenna systems with optional atmospheric refraction consideration.
Using effective Earth radius model (4/3 × actual Earth radius)
Calculation Result
Note: Results are theoretical under ideal conditions. Actual communication range may be affected by terrain, weather, and interference.
Antenna Height vs. Horizon Distance Relationship
Radio Horizon Principles
Understand the fundamental concepts, influencing factors, and calculation principles of radio horizon to better interpret and apply results.
What is Radio Horizon?
The radio horizon is the maximum distance over which radio waves can propagate in a straight line due to the curvature of the Earth. Beyond this point, the Earth's surface blocks further line-of-sight propagation.
Unlike the optical horizon, the radio horizon is typically farther because atmospheric refraction bends radio waves, effectively increasing the Earth's radius.
Antenna height is the most critical factor affecting radio horizon, with distance proportional to the square root of antenna height.
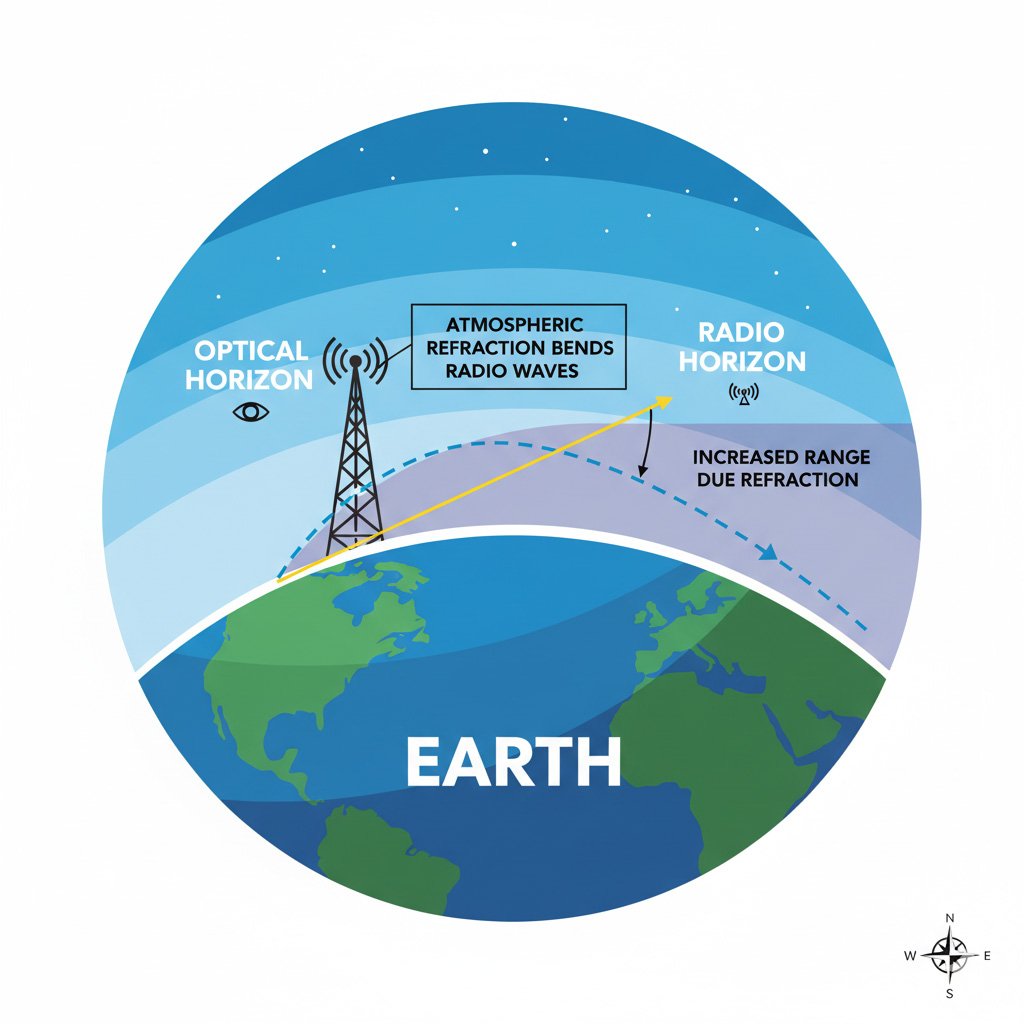
Radio wave propagation is affected by Earth's curvature – higher antennas achieve greater signal distance.
Antenna Height
Antenna height is the primary determinant of radio horizon. Higher antennas significantly increase propagation distance, though with diminishing returns due to the square root relationship.
Atmospheric Refraction
Atmospheric conditions affect radio wave paths. The effective Earth radius model (4/3 × actual radius) approximates atmospheric refraction effects.
Signal Frequency
Different frequencies respond differently to atmosphere and terrain. VHF/UHF bands follow line-of-sight, while HF bands can reflect off the ionosphere for longer distances.
Radio Horizon vs. Optical Horizon
| Characteristic | Radio Horizon | Optical Horizon |
|---|---|---|
| Calculation Formula | d ≈ 3.96 × √h | d ≈ 3.57 × √h |
| Atmospheric Effect | Significant, strongly affected by refraction | Less significant, primarily affected by visibility |
| Distance at Same Height | Farther | Closer |
| Primary Applications | Radio communication, radar, broadcasting | Optical observation, visual navigation |
Calculation Formulas & Derivation
Understand the mathematical principles and formulas behind radio horizon calculations for proper application in various scenarios.
Basic Formula
Where:
- d = Radio horizon distance (km)
- r = Earth's radius (approximately 6371 km)
- h = Antenna height (km)
This formula derives from geometric relationships, based on the right triangle formed by antenna height, Earth radius, and horizon distance.
Simplified Formula (meters)
Where:
- d = Radio horizon distance (km)
- h = Antenna height (meters)
This simplified version substitutes Earth's radius (6371 km) into the basic formula, ideal for quick estimates.
With Atmospheric Refraction
Where:
- d = Radio horizon distance (km)
- h = Antenna height (meters)
This formula uses effective Earth radius (approximately 8500 km, or 4/3 × actual radius) to approximate atmospheric refraction effects, better reflecting real-world conditions.
Dual Antenna System
Where:
- d1 = Transmit antenna horizon distance
- d2 = Receive antenna horizon distance
For point-to-point communication systems, total distance equals the sum of each antenna's individual horizon distances.
Formula Derivation Process
The radio horizon formula originates from basic geometric relationships. Considering Earth as a perfect sphere with an antenna at height h above its surface, the radio horizon is the distance to the point where signals just graze the Earth's surface.
Geometrically, the antenna position, Earth's center, and horizon point form a right triangle:
- Hypotenuse = Earth radius r + antenna height h: r + h
- One leg = Earth radius r
- Other leg = Radio horizon distance d
According to the Pythagorean theorem:
Expanding and simplifying:
d² = 2rh + h²
Since h is much smaller than r, the h² term can be neglected:
Substituting Earth's radius r = 6371 km and converting h to meters gives the simplified formula:
When considering atmospheric refraction using effective Earth radius (approximately 8500 km), the formula becomes:
Practical Applications
Explore real-world applications of radio horizon calculations across different fields and learn how to apply this knowledge to solve practical problems.
Amateur Radio
Ham radio operators use radio horizon calculations to plan communication ranges, select appropriate antenna heights and locations, and optimize communication effectiveness.
Typical Application:
In 10m band communications, a 20m high antenna provides approximately 16km line-of-sight range.
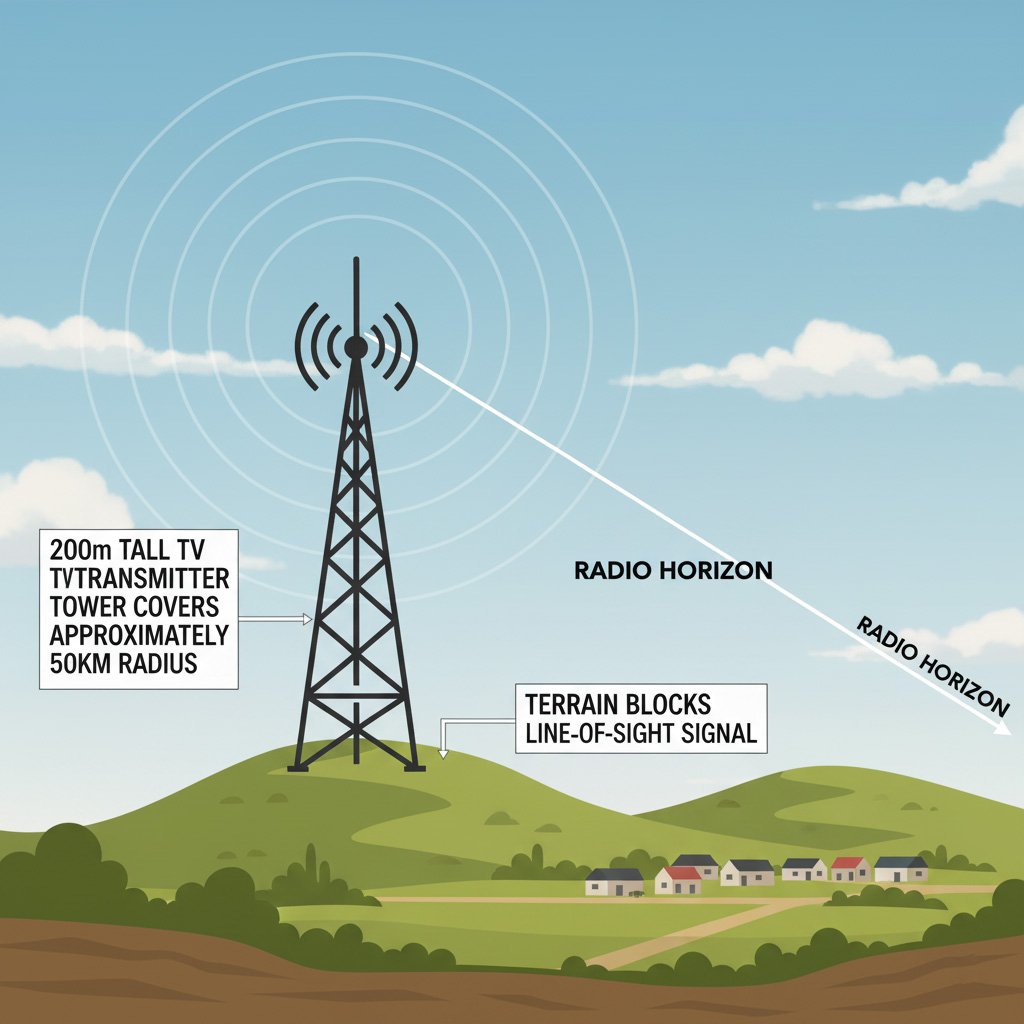
Broadcast Television
TV and radio stations use radio horizon calculations to determine transmitter coverage areas, optimize signal coverage, and minimize interference.
Typical Application:
A 200m tall TV transmitter tower can cover an area approximately 50km in radius.
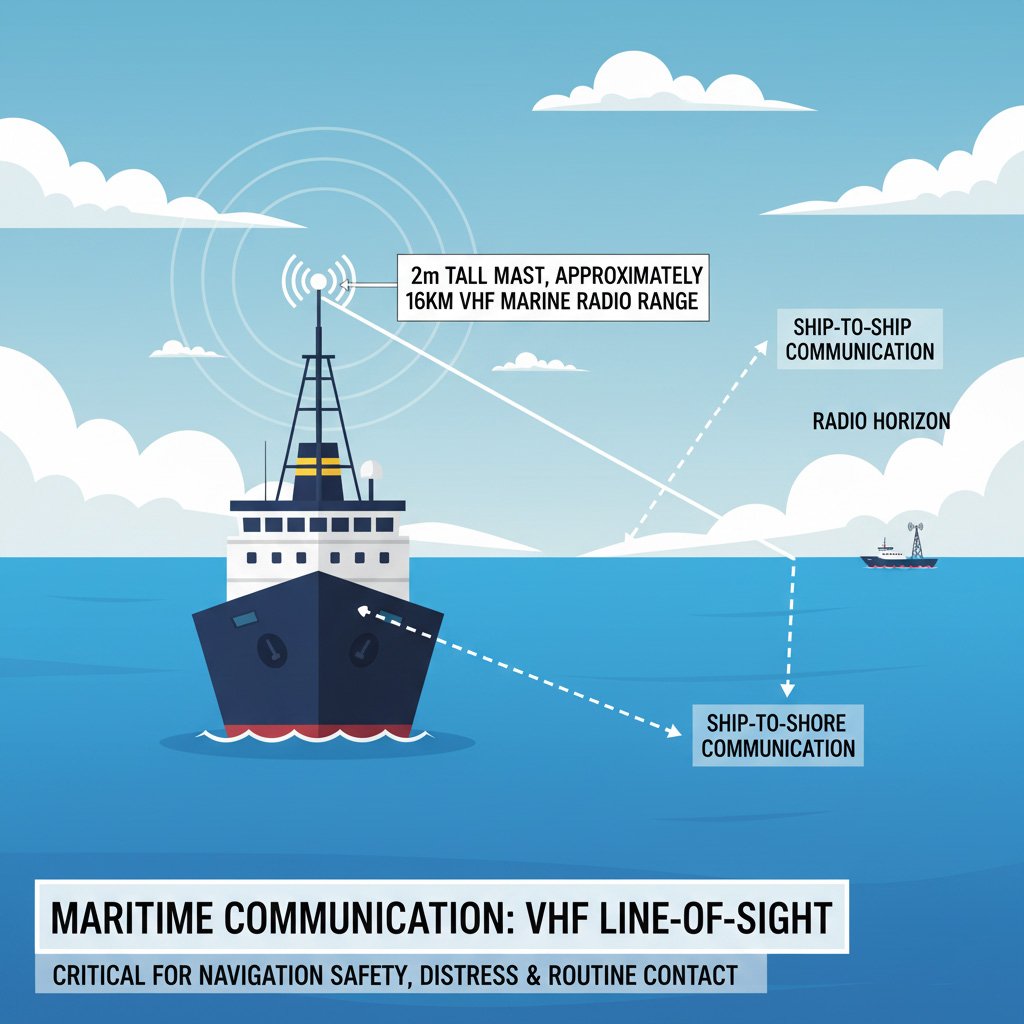
Maritime Communication
In maritime applications, radio horizon calculations plan ship-to-ship and ship-to-shore communications, ensuring navigation safety.
Typical Application:
A ship with a 20m tall mast has approximately 16km range for VHF marine radio.
Radar Systems
Radar engineers use horizon calculations to determine detection ranges, optimizing radar deployment and target detection capabilities.
Typical Application:
A 10m high radar antenna can detect 15m tall targets at approximately 11km.
Mobile Communications
Mobile network operators use radio horizon calculations to plan base station locations and heights, optimizing 5G/6G coverage and capacity.
Typical Application:
A 50m tall communication tower provides approximately 25km theoretical coverage.
Drone Communications
Drone operators use horizon calculations to determine safe communication ranges, preventing signal loss and vehicle out of control.
Typical Application:
A drone at 500m altitude can maintain line-of-sight communication with ground control up to approximately 70km.
Case Study: Intercity Communication Link Design
Problem: Establishing a VHF communication link between two cities 200km apart with a 75m transmit antenna. What receive antenna height is needed for line-of-sight communication?
Solution:
- Calculate transmit antenna radio horizon: d₁ = 3.96 × √75 ≈ 3.96 × 8.66 ≈ 34.3 km
- Calculate required receive antenna coverage: Required d₂ = 200 - 34.3 = 165.7 km
- Calculate required receive antenna height: h₂ = (d₂ / 3.96)² ≈ (165.7 / 3.96)² ≈ (41.8)² ≈ 1747 m
Conclusion: Since a 1747m receive antenna height is impractical, a relay station or alternative communication method (such as satellite communication) would be necessary to connect these two cities.
In practical applications, beyond antenna height considerations, factors like terrain obstacles, signal attenuation, and interference must be evaluated, potentially requiring field testing and adjustments.
Frequently Asked Questions
Answers to common questions about radio horizon calculations to help you better understand and apply this knowledge.
