PCB Trace Width Calculator

Welcome to the PCB Trace Width Calculator! This tool helps you determine the optimal width of a copper trace for your PCB design, ensuring it can safely carry a specified current without exceeding a desired temperature rise. By inputting your trace length, we can also estimate key electrical parameters such as resistance, voltage drop, and power loss, which are critical for efficient circuit performance. Please note that these results are based on standard IPC-2221 formulas and are estimates; real-world performance may vary depending on your unique application. For internal layers, you’ll likely need wider traces compared to surface traces, so be sure to select the appropriate calculation based on your design needs.

Internal Layer Results:

Required Trace Width (W):

Resistance:

Voltage Drop:

Power Loss:

External Layer Results:

Required Trace Width (W):

Resistance:

Voltage Drop:

Power Loss:

Understanding the IPC - 2221 Standard

The IPC – 2221 (and its updated version, IPC – 2221A) is the industry – recognized standard for PCB design. It provides empirical formulas for calculating trace width based on the following factors:

Current Carrying Capacity: The maximum current a trace can carry without overheating.
Temperature Rise: The increase in temperature due to the current flowing through the trace.
Copper Thickness: Thicker copper layers can handle more current.
Layer Type: External layers dissipate heat more effectively than internal layers.

The current – carrying capacity refers to the maximum current that a conductor (such as a PCB trace) can safely carry without generating excessive heat or causing damage. It mainly depends on the following factors:

Conductor Material: Different conductor materials have different resistivities. For example, copper is a commonly used conductor material in PCBs because it has a relatively low resistivity, allowing it to conduct larger currents with a smaller cross – sectional area.
Conductor Cross – Sectional Area: The larger the cross – sectional area, the lower the resistance of the conductor, and the greater the current it can carry. This is because a larger cross – sectional area provides more paths for electrons to flow, reducing the collision between electrons and atoms and thus lowering the resistance.
Heat Dissipation Conditions: Good heat dissipation conditions can effectively dissipate the heat generated by the conductor, thereby improving its current – carrying capacity. For example, in PCB design, heat dissipation layers and thermal vias can be added to improve heat dissipation.

When current passes through a conductor, due to the conductor’s resistance, heat is generated, causing the conductor’s temperature to rise. Temperature rise refers to the increase in the conductor’s temperature relative to the ambient temperature. The magnitude of the temperature rise mainly depends on the following factors:

Current Magnitude: According to Joule’s law $Q = I^{2} Rt$ (where $Q$ is heat, $I$ is current, $R$ is resistance, and $t$ is time), the larger the current, the more heat is generated, and the higher the temperature rise.
Conductor Resistance: The higher the resistance, the more heat is generated under the same current, resulting in a higher temperature rise.
Heat Dissipation Conditions: Good heat dissipation conditions can allow heat to be dissipated more quickly, thereby reducing the temperature rise.

IPC - 2221 Formulas:

According to the IPC-2221 standard, the key formulas are as follows:

Cross-Sectional Area:

A = \frac{I}{k \cdot ΔT b}

Variables:

A: Cross-sectional area (mm²)
I: Current (Amperes)
k: Material constant
0.024 for internal layers
0.048 for external layers
ΔT: Temperature rise (°C)
b: Empirical exponent (0.44 for ΔT ≤ 100°C)

Required Trace Width (W):

W = \frac{A}{T \cdot 1.378}

Variables:

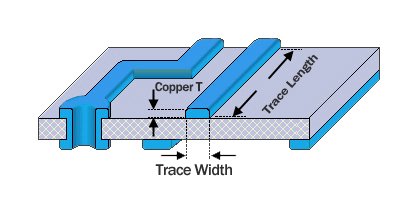
W:Trace width (mils)
A: Cross-sectional area from Formula 1 (mm²)
T: Copper thickness (oz/ft²)
1.378: Imperial conversion factor

Internal Layer Trace Width:

W = \frac{0.048 \cdot I^{0.44} \cdot T^{0.725}}{{ΔT}^{0.44}}

External Layer Trace Width:

W = \frac{0.024 \cdot I^{0.44} \cdot T^{0.725}}{{ΔT}^{0.44}}

Resistance:

R = ρ \cdot \frac{L}{T \cdot W} \cdot [1 + α \cdot (t e m p - 25)]

Variables:

R: Trace resistance (Ω)
ρ: Copper resistivity
- 1.72×10⁻⁸ Ω·m (standard)
- 2.44×10⁻⁸ Ω·m @ 100°C
L: Trace length (meters)
T: Copper thickness
- 1 oz/ft² = 0.0347 mm
- 2 oz/ft² = 0.0694 mm
W: Trace width (meters)
α: Temperature coefficient
- 0.00393/°C for copper
- ≈ 3900 ppm/°C
temp: Operating temperature (°C)

Voltage Drop:

V = I \cdot R = I \cdot \frac{ρ \cdot L}{A}

Variables:

V: Voltage drop (Volts)
I: Current (Amperes)
ρ: Copper resistivity
- 1.72×10⁻⁸ Ω·m @ 20°C
- Temperature adjusted value shown
L: Trace length
- In meters (SI units)
- 1 inch = 0.0254 m

Power Loss:

P = I^{2} \cdot R

Variables:

P: Power dissipation
- Unit: Watts (W)
- Critical for thermal management
- Max limit determined by PCB material
I: Current
- Unit: Amperes (A)
- RMS value for AC circuits
- Peak value consideration required
R: Trace resistance
- Unit: Ohms (Ω)
- Calculated by: $R = \frac{ρ \cdot L}{T \cdot W}$
- Temperature-dependent property

Environmental Conditions:

W_{adj} = W \cdot {(1 + \frac{RH}{100})}^{0.25}

Variables:

W_adj: Adjusted trace width
W: Base width from Formula 2
RH: Relative humidity (%)
0.25: Environmental factor exponent

Derivation of the IPC - 2221 Equation

IPC – 2221 is a general standard for printed circuit board (PCB) design. The equation for calculating trace width in it is derived based on experimental data and theoretical analysis.

Basic Principle

The derivation of this equation is based on the principle of thermal equilibrium of the conductor, that is, the heat generated by the conductor is equal to the heat dissipated. When the conductor reaches thermal equilibrium, the temperature rise remains stable.

Derivation Process

Step1: Heat Generation

According to Joule's law, when a current $I$ passes through a conductor with resistance $R$ , the heat generated per unit time $P_{gen}$ is given by the formula:

P_{gen} = I^{2} R

Step2: Heat Dissipation

Heat dissipation mainly occurs through convection and radiation. For PCB traces, convection is the main heat - dissipation method. The power of convective heat dissipation $P_{diss}$ can be expressed as:

P_{diss} = h A Δ T

where $h$ is the convective heat - transfer coefficient, $A$ is the heat - dissipation area of the conductor, and $Δ T$ is the temperature rise.

Step3: Thermal Equilibrium

When thermal equilibrium is reached, the heat generated equals the heat dissipated, so we have:

P_{gen} = P_{diss}

Substituting the expressions for $P_{gen}$ and $P_{diss}$ , we get $I^{2} R = h A Δ T$ .

Resistance Calculation

The resistance of the conductor $R$ is calculated using the formula:

R = ρ \frac{l}{A_{c}}

where $ρ$ is the resistivity of the conductor, $l$ is the length of the conductor, and $A_{c}$ is the cross - sectional area of the conductor.

Step5: Trace Width Calculation

Substituting $R$ into the thermal equilibrium equation and after a series of experimental data fitting and corrections, the formula for calculating the trace width $W$ in IPC - 2221 is obtained.

For internal layer traces:

W = \frac{0.048 \times I^{0.44} \times T^{0.725}}{{Δ T}^{0.44}}

For external layer traces:

W = \frac{0.024 \times I^{0.44} \times T^{0.725}}{{Δ T}^{0.44}}

where $W$ is the trace width (in inches), $I$ is the current (in amperes), $T$ is the copper foil thickness (in ounces per square foot), and $Δ T$ is the temperature rise (in degrees Celsius).

Factors Affecting Trace Width

While the IPC – 2221 standard serves as a solid foundation, there are additional factors to consider:

Environmental Conditions:

Altitude: At higher altitudes, the air is thinner, which reduces heat dissipation.
Enclosures: Traces inside enclosed spaces may not cool as effectively.
Conformal Coatings: These coatings can insulate the trace and affect heat transfer.

Material Properties:

Resistivity: Different copper alloys have different electrical resistivities.
Trace Geometry: Wide and short traces are more efficient at handling current.

Design Goals:

Signal Integrity: Narrow traces can cause impedance mismatches in high – frequency circuits.
Power Integrity: Thick traces are essential for minimizing voltage drops in power – delivery networks.

How to Use the Calculator Effectively?

Determine Your Design Requirements: Decide on the maximum current, temperature rise, and operating environment.
Input Parameters: Enter the values into the calculator. Use the “Advanced” mode for detailed calculations.
Review the Results: Check the trace width and electrical parameters. Adjust the inputs if necessary.
Validate with Your Manufacturer: Confirm the results with your PCB fabricator to ensure manufacturability.

Common Questions Answered

Q: Can I use the calculator for high - voltage designs?

A: Yes, but also refer to safety standards like IPC – 2221 for creepage and clearance.

Q: What if my PCB has multiple layers?

A: Use the calculator for each layer separately, considering the thermal properties of each.

Q: How accurate are the results?

A: The calculator provides estimates. Always conduct thermal simulations for critical designs.

PCB Trace Width Calculator

Understanding the IPC - 2221 Standard

IPC - 2221 Formulas:

Derivation of the IPC - 2221 Equation

Basic Principle

Derivation Process

Step1: Heat Generation

Step2: Heat Dissipation

Step3: Thermal Equilibrium

Resistance Calculation

Step5: Trace Width Calculation

Factors Affecting Trace Width

Environmental Conditions:

Material Properties:

Design Goals:

How to Use the Calculator Effectively?

Common Questions Answered

Our PCB Services

Resources

Contact

PCB Trace Width Calculator

Understanding the IPC - 2221 Standard

IPC - 2221 Formulas:

Derivation of the IPC - 2221 Equation

Basic Principle

Derivation Process

Step1: Heat Generation

Step2: Heat Dissipation

Step3: Thermal Equilibrium

Resistance Calculation

Step5: Trace Width Calculation

Factors Affecting Trace Width

Environmental Conditions:

Material Properties:

Design Goals:

How to Use the Calculator Effectively?

Common Questions Answered

Our PCB Services

Resources

Contact

Instant Quote