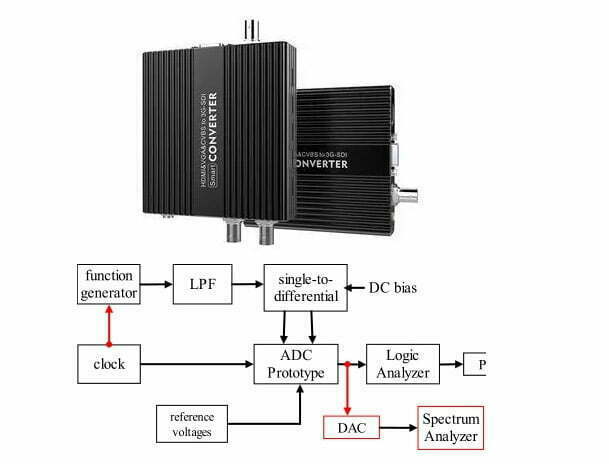
Parmi les instruments intelligents, les convertisseurs ADC et DAC jouent un rôle essentiel. Nous savons que les microprocesseurs largement utilisés actuellement ne peuvent traiter que des signaux numériques discrets. Il n’est pas possible d’alimenter un signal analogique continu provenant du monde physique dans un microprocesseur sans un ADC. De même, sans un DAC, il n’est pas possible de sortir un signal analogique d’un microprocesseur. (cliquez ici pour en savoir plus sur le signal numérique et le signal analogique)
Convertisseur analogique-numérique (ADC)
Définition de l'ADC
Dans le système d’instrumentation, il est souvent nécessaire de convertir les quantités analogiques continuellement changeantes détectées, telles que la température, la pression, le débit, la vitesse, l’intensité lumineuse, etc., en quantités numériques discrètes avant de les introduire dans l’ordinateur pour traitement. Ces quantités analogiques sont converties en signaux électriques (généralement des signaux de tension) par des capteurs, et après avoir été amplifiées par des amplificateurs, elles doivent subir un certain traitement pour devenir des quantités numériques. Un dispositif qui convertit l’analogique en numérique est généralement appelé convertisseur analogique-numérique (ADC), ou A/D en abrégé.
Principe de fonctionnement de l'ADC
Dans des circonstances normales, la conversion A/N doit généralement passer par quatre processus d’échantillonnage, de maintien, de quantification et d’encodage.
Échantillonnage et maintien
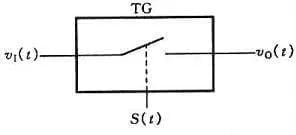
L’échantillonnage consiste à convertir une quantité analogique qui varie continuellement dans le temps en une quantité analogique discrète dans le temps. Le schéma du processus d’échantillonnage est présenté à la Figure 1. La Figure (a) est une structure de circuit d’échantillonnage, dans laquelle la porte de transmission est contrôlée par le signal d’échantillonnage S(t), pendant la largeur d’impulsion τ de S(t), la porte de transmission est activée, le signal de sortie vO(t) est le signal d’entrée v1, et pendant (Ts-τ), la porte de transmission est fermée et le signal de sortie vO(t)=0. Les formes d’onde des signaux dans le circuit sont présentées à la Figure (b).
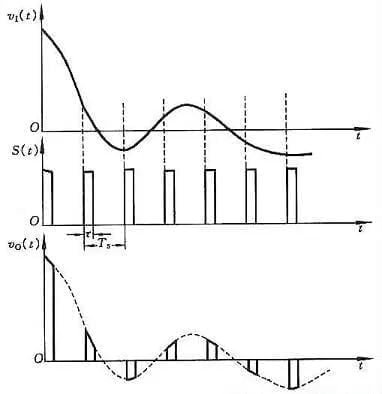
Il ressort de l’analyse que plus la fréquence du signal d’échantillonnage S(t) est élevée, plus le signal obtenu peut reproduire fidèlement le signal d’entrée après être passé par le filtre passe-bas. Mais le problème est que la quantité de données augmente. Afin de garantir une fréquence d’échantillonnage appropriée, elle doit satisfaire le théorème d’échantillonnage.
Théorème d’échantillonnage : Supposons que la fréquence du signal d’échantillonnage S(t) soit fs, et que la fréquence de la composante de fréquence la plus élevée du signal analogique d’entrée v1(t) soit fimax, alors fs et fimax doivent satisfaire la relation suivante fs≥2fimax, et fs> est généralement pris en ingénierie (3~5) fimax.
Il faut un certain temps pour convertir le signal analogique obtenu par le circuit d’échantillonnage en un signal numérique à chaque fois. Afin de fournir une valeur stable pour le processus de quantification et d’encodage ultérieur, le signal analogique obtenu à chaque fois doit être maintenu pendant un certain temps par le circuit de maintien.
Le processus d’échantillonnage et de maintien est souvent réalisé simultanément par le circuit d’échantillonnage-maintien. Le schéma et la forme d’onde de sortie du circuit d’échantillonnage-maintien sont présentés à la Figure 2.
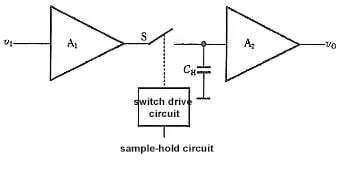
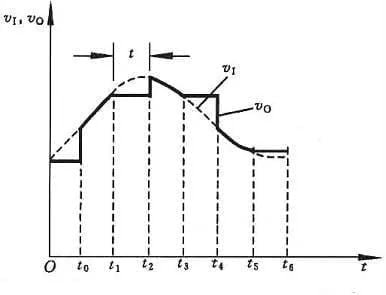
Le circuit est composé d’un amplificateur d’entrée A1, d’un amplificateur de sortie A2, d’un condensateur de maintien CH et d’un circuit de commande de commutateur. A1 doit avoir une impédance d’entrée élevée dans le circuit afin de réduire l’influence sur la source du signal d’entrée. Afin de rendre difficile la décharge de la charge stockée sur CH pendant la phase de maintien, A2 doit également avoir une impédance d’entrée élevée, et A2 doit également avoir une impédance de sortie faible, ce qui peut améliorer la capacité de charge du circuit. Généralement, il est également requis que AV1⋅AV2=1 dans le circuit.
Analysons maintenant, en conjonction avec la figure 2, le principe de fonctionnement de l’échantillonnage et du maintien du circuit. À t=t0, l’interrupteur S est fermé et le condensateur est chargé rapidement. Puisque AV1 ⋅ AV2=1, v0=vI, la période d’échantillonnage se situe pendant l’intervalle de temps de t0⩽t1. Au temps t=t1, S est déconnecté. Si l’impédance d’entrée de A2 est infinie et que S est un interrupteur idéal, on peut considérer que le condensateur CH n’a pas de circuit de décharge et que la tension à ses bornes reste constante à v0. La section plate de t1 à t2 dans la figure 11.8.2(b) est la phase de maintien.
Le circuit d’échantillonnage et de maintien peut être produit par divers types de circuits intégrés monolithiques. Par exemple, il existe AD585 et AD684 pour la technologie bipolaire ; AD1154 et SHC76 pour la technologie mixte.
Quantification et codage
Les signaux numériques sont non seulement discrets dans le temps, mais aussi discontinus en amplitude. La taille de toute quantité numérique ne peut être qu’un multiple entier d’une unité de quantité minimale spécifiée. Afin de convertir le signal analogique en une quantité numérique, dans le processus de conversion A/D, la tension de sortie du circuit d’échantillonnage-maintien doit également être normalisée au niveau discret correspondant d’une certaine manière approximative. Ce processus de conversion est appelé quantification numérique, désignée par le terme de quantification. La valeur quantifiée doit finalement être représentée par un code grâce au processus d’encodage. Le code obtenu après l’encodage est la quantité numérique fournie en sortie par le convertisseur A/D.
L’unité de quantité minimale prise dans le processus de quantification est appelée unité de quantification, représentée par △. Il s’agit de la quantité analogique correspondant au moment où le bit de poids faible du signal numérique est à 1, c’est-à-dire 1LSB.
Dans le processus de quantification, étant donné que la tension d’échantillonnage n’est pas nécessairement divisible par △, il y a inévitablement une erreur avant et après la quantification. Cette erreur est appelée erreur de quantification et est représentée par ε. L’erreur de quantification est une erreur de principe qui ne peut être éliminée. Plus le convertisseur A/D a de bits, plus la différence entre les niveaux discrets est faible et plus l’erreur de quantification est faible.
Deux méthodes de quantification approximatives sont souvent utilisées dans le processus de quantification : la quantification par arrondi uniquement et la quantification par arrondi.
seulement arrondir la méthode de quantification
Prenons l’exemple du convertisseur A/N 3 bits, supposons que le signal d’entrée v1 varie de 0 à 8V. En utilisant la méthode de quantification par arrondi supérieur, on prend △=1V, et on élimine la partie qui n’est pas suffisante dans l’unité de quantification. Si la valeur est comprise entre 0 et 8V, la tension analogique entre 1V est considérée comme 0△, représentée par le nombre binaire 000, et la tension analogique entre 1V et 2V est considérée comme 1△, représentée par le nombre binaire 001… L’erreur maximale de cette méthode de quantification est △.
méthode de quantification par arrondi
Si la méthode de quantification par arrondi est adoptée, l’unité de quantification △=8V/15 est utilisée, et la partie inférieure à la moitié de l’unité de quantification sera éliminée pendant le processus de quantification, et la partie égale ou supérieure à la moitié de l’unité de quantification sera traitée comme une unité de quantification. Elle traite la tension analogique entre 0 ~ 8V/15 comme 0△, représentée par 000 en binaire, et la tension analogique entre 8V/15 ~ 24V/15 est considérée comme 1△, représentée par le nombre binaire 001 signifie attendre.
Comparaison
L’erreur de quantification maximale│εmax│=1LSB dans la première méthode de quantification avec arrondi uniquement, et la méthode de quantification│εmax│=1LSB/2 dans la dernière méthode de quantification avec arrondi et arrondi, l’erreur de quantification de la dernière est inférieure à la première, elle est donc utilisée par la majorité des convertisseurs A/N.
Avec le développement rapide des circuits intégrés, de nouvelles idées de conception et de nouvelles techniques de fabrication pour les convertisseurs A/N apparaissent sans cesse. Des convertisseurs A/N avec différentes structures et performances sont conçus pour répondre à divers besoins de détection et de contrôle.
Types de ADC
ADC Intégrateur
principe de conversion
Le principe de conversion de l’intégration ADC est basé sur l’intégration de la tension et la comparaison de la tension intégrée avec une autre tension pour contrôler le comptage, et la sortie du comptage est la sortie ADC. L’objet de l’intégration est soit basé sur la tension de référence, soit basé sur la tension de référence et la tension d’entrée.
Avantages et inconvénients
Avantages :
- L’ADC intégrateur a une haute résolution, et le nombre de chiffres peut être de 12 ou plus.
- La linéarité est très bonne. Essentiellement, l’entrée est comparée à une tension de référence intégrée pour déterminer la sortie, de sorte que la linéarité dépendra de la précision du comparateur.
- La topologie de réalisation du circuit est simple, et il y a relativement peu de composants utilisés pour réaliser ces dispositifs, de sorte que le circuit est relativement simple et le coût de production est faible.
Inconvénient :
- Le principal inconvénient est la lenteur de la conversion. ADC N bits, la sortie peut prendre jusqu’à 2 N cycles d’horloge pour convertir un seul point d’échantillon.
Applications
Principalement utilisé dans les applications de capteurs et les dispositifs tels que les voltmètres et les ampèremètres où la précision est plus importante que la vitesse. En d’autres termes, la vitesse d’échantillonnage de l’ADC intégrateur est relativement faible, mais la précision est très élevée.
classification
Il existe différents types d’ADC intégrateurs, et les plus courants sont les intégrateurs à simple et double pente. Ajouter une « pente » augmente la précision au détriment du temps de conversion.
ADC intégrateur à simple pente
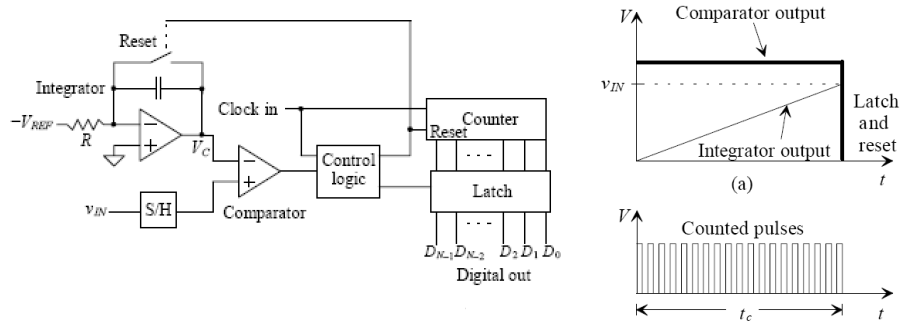
Le comparateur compare la tension d’entrée à la valeur de la tension de référence intégrée (notez que nous la rendrons négative car elle est connectée à l’entrée inverseuse de l’amplificateur opérationnel). Comptez simultanément le nombre de cycles d’horloge. Lorsque la sortie de l’intégrateur est égale, le comparateur émet une logique « 0 », déclenchant une réinitialisation du compteur et de l’intégrateur, et le verrou maintient la sortie numérique.
VINVREFVrefVrefVin
C’est le temps de conversion. Je sais pourquoi ce ADC intégral est lent. Examinons le pire des cas, en supposant la tension d’entrée, en supposant, en supposant qu’il s’agit d’un ADC 20 bits, alors !
VIN=VREFTCLK=1ustc=220us=1048576us
ADC intégral à pente unique
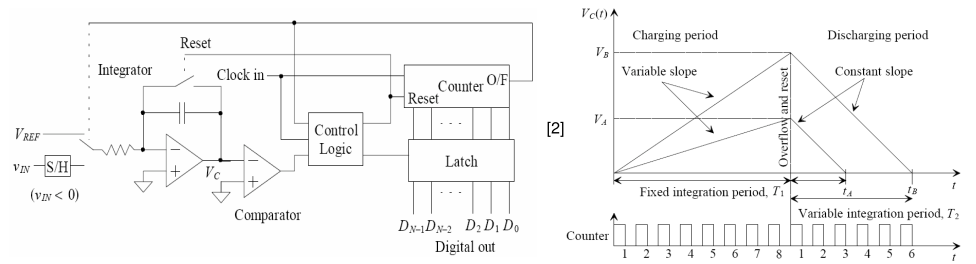
Un ADC à double pente diffère d’un ADC à simple pente en ce sens que la comparaison au sol est maintenant effectuée et que deux sommes de tensions sont intégrées. Initialement, l’entrée négative est connectée à l’intégrateur, qui augmente jusqu’à ce que le compteur déborde. Étant donné que l’intégration à l’entrée inverseuse passe à une valeur négative, la sortie de l’intégrateur sera toujours positive et supérieure à zéro, de sorte que le compteur continuera à fonctionner jusqu’à ce qu’il déborde, ce qui prend 2N cycles d’horloge (=T1).
VCVREFVINVC
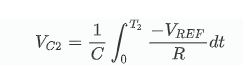
Au temps T2, il sera égal à la somme de et, et il
VC=VC1+VC2=0
Mais:
VIN/VREF=T2/T1
Par conséquent, le principe de conversion ADC, l’ADC à double pente est plus lent que l’ADC à simple pente, car l’intégration est effectuée deux fois, l’erreur liée à la pente de l’intégrateur sera annulée, améliorant ainsi la précision en principe.
Sigma-Delta Σ-Δ ADC
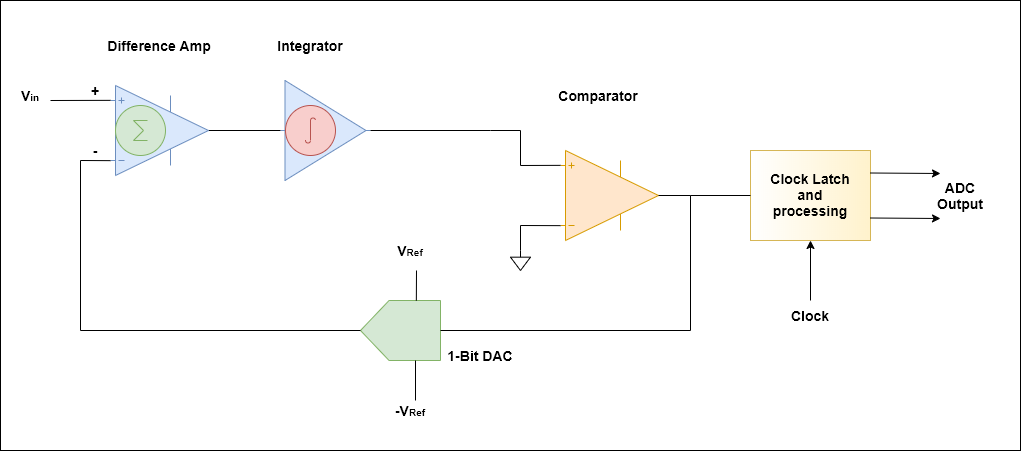
En partant de l’entrée, l’amplificateur différentiel produit une sortie qui est la différence entre Vin et la sortie du DAC 1 bit. La sortie d’un DAC 1 bit peut prendre l’une de deux valeurs : OR . Dans cette topologie, un intégrateur peut être considéré comme prenant une moyenne mobile de la valeur précédente et de la valeur d’entrée actuelle.
–Vref+Vref
Par conséquent, en supposant que le segment positif du comparateur est initialement fixé à une petite valeur supérieure à 0V, le comparateur s’inverse. Sa valeur sera élevée ou 1. Ensuite, la sortie du DAC sera . Lors de l’itération suivante, cette valeur sera soustraite de la valeur actuelle de . Puisque la valeur précédente était de 0V, la sortie de l’intégrateur sera maintenant – Vref. À ce stade, la sortie du comparateur sera de 0 et la sortie du DAC sera .
+VrefVin-Vref
Lors de l’échantillon suivant, la sortie de l’intégrateur sera de 0 en raison de la valeur précédente, et l’amplificateur différentiel soustraira en fait , ajoutant ainsi à . La sortie du comparateur sera de 1.
-Vref-Vref+VrefVin
Ce processus se poursuit de manière itérative, de sorte que, pour une entrée de 0V, la sortie du comparateur sera un flux régulier de 101010…. Rappelez-vous que la logique 1 signifie , la logique 0 signifie , donc si N échantillons sont échantillonnés et moyennés, il est facile de voir que la valeur moyenne est de 0V. Le bloc de traitement après le comparateur affichera simplement cela comme une seule valeur 0000…, en supposant une valeur de référence de ( ~ ) ou 2 x.
+Vref-Vref-Vref+VrefVref
Maintenant, en supposant 1V, il s’agit d’un ADC 5V. est ±2.5V. En suivant les mêmes étapes qu’avant de manière itérative, la sortie sera : 1011101… La sortie est de 1.07V.
Vin±Vref
En résumé :
Un ADC sigma-delta suréchantillonne le signal traité (voir Comment l’échantillonnage analogique-numérique pour ce concept) et filtre passe-bas le signal à traiter. Habituellement, le nombre de bits convertis à l’aide de l’ADC Flash après le filtre est inférieur au nombre de bits requis. Le signal résultant, ainsi que les erreurs des niveaux discrets FLASH, sont renvoyés et soustraits de l’entrée et alimentés au filtre. Cette rétroaction négative atténue le bruit afin qu’il n’apparaisse pas à la fréquence du signal souhaitée. Un filtre numérique après l’ADC (utilisant un filtre de décimation) réduit la fréquence d’échantillonnage, filtre les signaux de bruit indésirables et augmente la résolution de sortie (d’où le nom de modulation sigma-delta, également connue sous le nom de modulation delta-sigma).
ADC Flash (type à comparaison directe)
Le principe de l’ADC FLASH est peut-être le plus facile à comprendre. La figure ci-dessous est un schéma d’un ADC 2 bits, qui se compose de nombreux comparateurs, chacun étant doté d’une tension de référence qui est un bit plus élevée que la valeur de référence précédente. Par conséquent, pour un ADC 8 bits, 256 de ces comparateurs sont nécessaires. Pour 10 bits, vous en avez besoin de 1024.
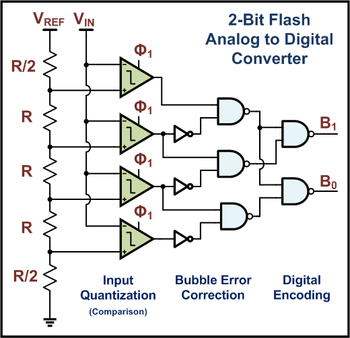
L’ADC FLASH (type à comparaison directe) est rapide. Il convertit directement l’entrée sans échantillonnage ni post-traitement lourd. Le problème est qu’il nécessite beaucoup de comparateurs, et beaucoup de comparateurs prennent beaucoup de place sur la puce. Par conséquent, n’utilisez les ADC Flash que lorsque vous avez besoin de vitesses extrêmement élevées qui ne peuvent pas être atteintes avec d’autres implémentations d’ADC.
Dichotomie incarnée dans le matériel
Dans les applications pratiques, il existe une autre variante plus couramment utilisée, le ADC semi-FLASH. Il utilise un processus en deux étapes pour réduire le nombre de convertisseurs nécessaires dans la chaîne de conversion réelle :
Tout d’abord, le signal d’entrée est comparé à l’ensemble des niveaux qui se situent exactement à la moitié. S’il est inférieur, le bit de poids fort (MSB) est défini sur 0 et l’entrée est transmise à une chaîne de comparateurs avec la tension de référence réglée pour convertir le reste des bits.
Si le signal d’entrée est supérieur, définissez le MSB sur 1, soustrayez de le signal d’entrée. La chaîne de comparateurs est à nouveau utilisée pour obtenir les bits restants. Ainsi, en essence, l’ADC semi-FLASH à demi-pas sacrifie une comparaison supplémentaire pour économiser la moitié du comparateur. Ce type de raisonnement peut également continuer à être déduit et étendu, comme l’ADC FLASH à 4 points et ainsi de suite
Le registre à approximation successive (SAR)
Le registre à approximation successive (SAR) est un élément essentiel du convertisseur analogique-numérique à approximation successive. Il fonctionne en utilisant un comparateur pour réduire progressivement la zone contenant la tension d’entrée. Pour ce faire, le convertisseur compare la tension d’entrée à la sortie d’un convertisseur numérique-analogique, qui indique généralement le milieu de la plage de tension choisie. À chaque étape du processus, l’estimation est stockée dans le SAR.
Par exemple, supposons que la tension d’entrée est de 6,3 V et que la plage initiale est de 0 à 16 V.
- Pour la première étape, entrez 6,3 V pour comparer avec 8 V (le point médian de la plage de 0 à 16 V). Le comparateur indique une tension d’entrée inférieure à 8 V, de sorte que le SAR est mis à jour pour réduire la plage à 0 – 8 V.
- Dans la deuxième étape, la tension d’entrée est comparée à 4 V (le point médian de 0 – 8 V), le comparateur indique que la tension d’entrée est supérieure à 4 V, de sorte que le SAR est mis à jour pour refléter que la tension d’entrée se situe dans la plage de 4 à 8 V.
- Dans la troisième étape, la tension d’entrée est comparée à 6 V (la moitié de 4 V à 8 V) ; le comparateur indique une tension d’entrée supérieure à 6 volts, et la plage de recherche devient de 6 à 8 volts.
Continuez ces étapes jusqu’à ce que vous atteigniez la solution souhaitée. Sa topologie est la suivante:
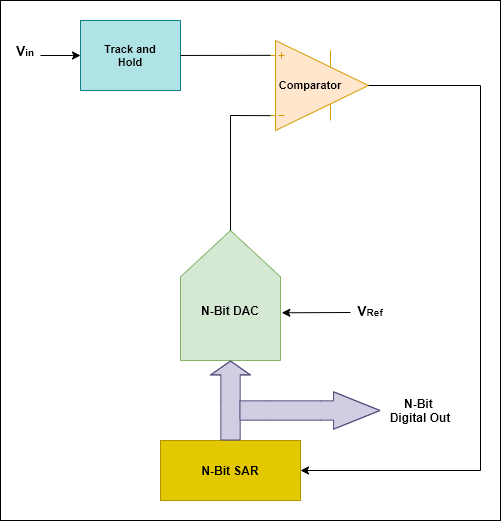
Pour l’intuition, regardez l’animation suivante:
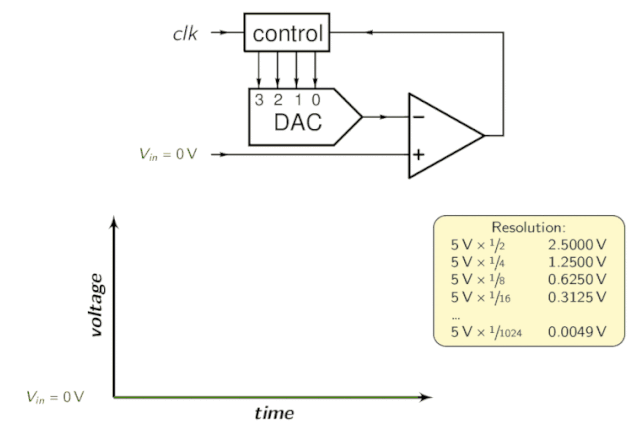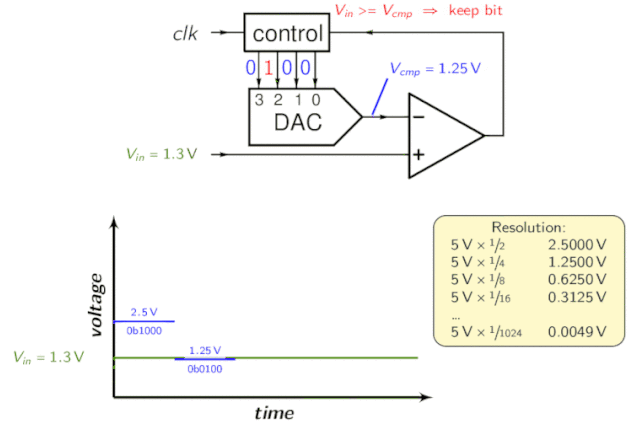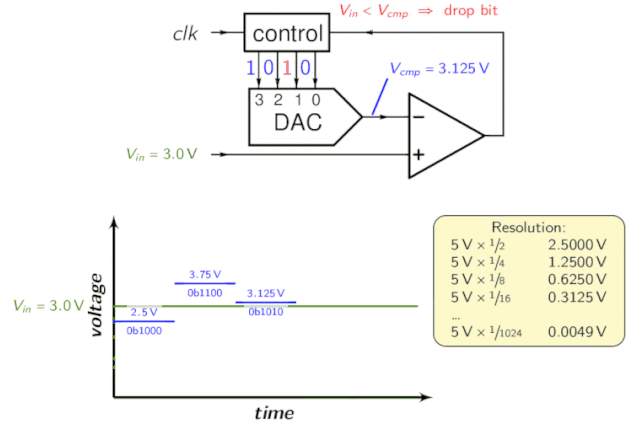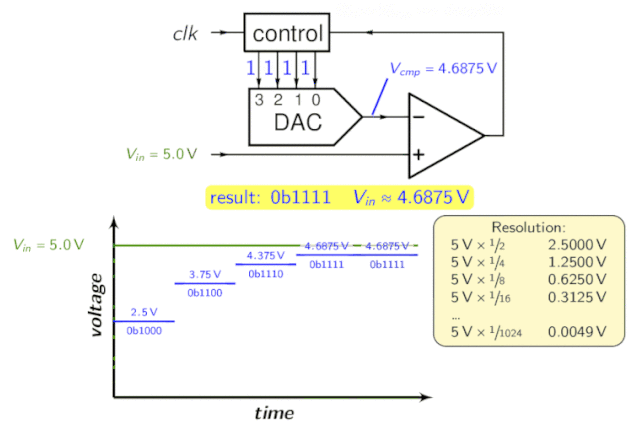
Convertisseur ADC à pipeline
Un ADC à pipeline (également connu sous le nom de quantificateur de sous-routine) utilise deux pipelines ou plus. Tout d’abord, effectuez une conversion approximative. Dans la deuxième étape, un convertisseur numérique-analogique (DAC) est utilisé pour déterminer la différence dans le signal d’entrée. Cette différence est ensuite convertie en valeurs plus fines et les résultats sont combinés dans une étape finale. Cela peut être considéré comme une amélioration par rapport aux ADC à approximation successive, où le signal de référence de rétroaction consiste en des transitions intermédiaires sur l’ensemble de la plage de bits (par exemple, 4 bits), plutôt que seulement le bit significatif suivant. Combinant les avantages de la méthode d’approximation successive et de l’ADC flash, ce type présente les avantages d’une grande vitesse, d’une haute résolution et d’une petite taille de moule.
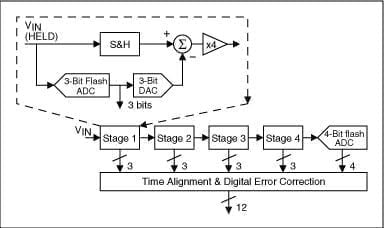
Dans ce schéma, l’entrée analogique VIN est d’abord échantillonnée et maintenue stable par un échantillonneur-bloqueur (S&H), tandis que l’ADC flash au premier étage la quantifie en trois bits. La sortie 3 bits est ensuite envoyée à un DAC 3 bits (précision 12 bits) et la sortie analogique est soustraite de l’entrée. Ce « reste » est amplifié par un facteur de 4 et envoyé à l’étape suivante (étape 2). Ce reste ajouté continue à travers les étages inférieurs du pipeline, fournissant 3 bits par étage, jusqu’à ce qu’il atteigne l’ADC flash 4 bits, qui résoudra les 4 bits de poids faible (4LSB) finaux. Étant donné que les bits de chaque étage sont déterminés à différents moments, tous les bits correspondant au même échantillon sont alignés dans le temps avec le registre à décalage avant d’être envoyés à la logique de correction d’erreur numérique. Notez que lorsqu’un pipeline a terminé de traiter les échantillons d’entrée, en déterminant le bit d’acquisition pour ce pipeline et en transmettant le résidu au pipeline suivant, il peut commencer à traiter le prochain échantillon reçu à partir du maintien d’échantillon intégré dans chaque pipeline. Ce pipelining est la raison du débit élevé, qui est également le concept de pipelining.
Autres
En plus des ADC courants mentionnés ci-dessus, il existe également des ADC basés sur le principe de l’équilibre de charge, des ADC à multiplexage temporel, des ADC FM, des ADC à étirement temporel, des ADC à codage incrémental, des ADC Wilkinson, etc.
Convertisseur Numérique-Analogique (CNA)
Définition du CNA
La quantité numérique traitée par le système numérique doit parfois être convertie en une quantité analogique pour une utilisation pratique. Cette conversion est appelée « conversion numérique-analogique ». Le circuit qui effectue la conversion numérique-analogique est appelé convertisseur numérique-analogique, ou CNA (Convertisseur Numérique-Analogique) en abrégé.
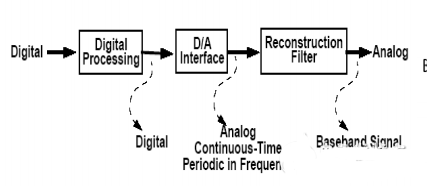
Paramètres du CNA
Résolution
La résolution dans un CNA est définie comme le nombre de tous les niveaux analogiques de sortie possibles pour différentes valeurs de code numérique en entrée. Une résolution de N bits signifie que le CNA peut générer 2N-1 niveaux analogiques différents. Généralement, cela fait référence au nombre de chiffres du code numérique en entrée.
Erreurs d'offset et de gain
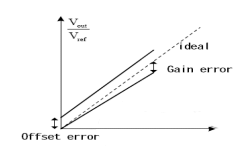
L’offset est défini comme la valeur du signal analogique de sortie réel lorsqu’une valeur de code de 0 est entrée, et l’erreur de gain est définie comme la différence entre la valeur de sortie à pleine échelle idéale et la valeur de sortie réelle après déduction de l’offset, comme le montre la figure.
Précision
La précision dans un DAC est divisée en précision absolue et précision relative. La précision absolue est définie comme la différence entre la sortie idéale et la sortie réelle, incluant divers décalages et erreurs non linéaires. La précision relative est définie comme l’erreur non linéaire intégrale maximale. La précision est exprimée comme un rapport de la pleine échelle, exprimé en chiffres effectifs. Par exemple, une précision de 8 bits signifie que l’erreur du DAC est inférieure à 1/8 de la sortie à pleine échelle du DAC. Notez que le concept de précision n’est pas lié à la résolution. Un DAC avec une résolution de 12 bits peut n’avoir qu’une précision de 10 bits ; et un DAC avec une résolution de 10 bits peut avoir une précision de 12 bits. La précision par rapport à la résolution signifie que la réponse de transmission du DAC peut être contrôlée plus précisément.
INL - Non-linéarité intégrale
Une fois les erreurs de décalage et de gain supprimées, l’erreur de linéarité intégrale est définie comme la déviation de la caractéristique de transfert réelle de la caractéristique de transfert idéale (une ligne droite). comme le montre l’image.
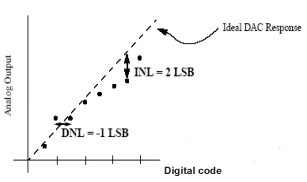
DNL - Non-linéarité différentielle
Dans un DAC idéal avec un minimum de 1 LSB par changement de sortie analogique, l’erreur de non-linéarité différentielle est définie comme la déviation de 1 LSB par changement de sortie analogique minimum (à l’exclusion de l’erreur de gain et du décalage). Le DNL que nous définissons concerne chaque valeur de code d’entrée numérique, et parfois le DNL le plus grand est utilisé pour définir le DNL de l’ensemble du DAC. Un DAC idéal aurait une erreur de non-linéarité différentielle nulle pour chaque entrée numérique, tandis qu’un DAC avec un DNL maximal de 0,5 LSB aurait un changement de sortie minimum entre 0,5 LSB et 1,5 LSB par sortie. Les erreurs de linéarité intégrale et différentielle du DAC sont illustrées dans la figure.
Énergie de gigue (Surface d'impulsion de gigue)
La surface maximale sous la gigue qui apparaît à la sortie après que le signal d’entrée change.
Temps de stabilisation
Le temps de stabilisation se situe dans une plage d’erreur spécifique de la valeur finale, et le temps nécessaire pour que la sortie subisse une conversion à pleine échelle.
Monotonicité Un DAC monotone est un DAC dans lequel le niveau analogique de sortie augmente toujours lorsque la valeur du code numérique d’entrée augmente. Si le DNL maximum est contrôlé dans une plage de 0,5 LSB, alors la monotonicité du DAC peut être naturellement garantie.
Plage dynamique sans échelon (SFDR) SFDR est la plage dynamique sans échelon, c’est-à-dire la plage dynamique sans bruit ni harmoniques. Le bruit et les harmoniques sont appelés signaux parasites.
Principe du DAC
Convertir chaque code binaire d’entrée en une quantité analogique correspondante en fonction de son poids, puis additionner les quantités analogiques représentant chaque bit. La quantité analogique totale obtenue est proportionnelle à la quantité numérique, réalisant ainsi la conversion de la quantité numérique à la quantité analogique.
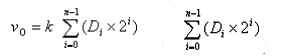
C’est la valeur décimale convertie en un nombre binaire par expansion du poids des bits.
Composition et caractéristiques du DAC
Un DAC est principalement composé de registres numériques, de commutateurs électroniques analogiques, d’un réseau de poids binaires, d’un amplificateur opérationnel de sommation et d’une source de tension de référence (ou d’une source de courant constant). Les chiffres des quantités numériques stockées dans le registre numérique sont utilisés pour contrôler les commutateurs électroniques analogiques des chiffres correspondants, de sorte que le chiffre avec un chiffre de 1 génère une valeur de courant proportionnelle à son poids de chiffre sur le réseau de poids de chiffre, puis l’amplificateur opérationnel contrôle chaque valeur de courant sommée et convertie en une valeur de tension.
La variation des réseaux de poids binaires permet l’assemblage de plusieurs types de DAC, notamment le DAC à réseau de résistance pondérée, le DAC à réseau de résistance inversé en T en R-2R et le DAC à réseau de courant à valeur unique, etc. La précision de la conversion produite par le DAC à réseau de résistance pondérée dépend de la précision de la tension de référence VREF, ainsi que de la qualité des commutateurs électroniques analogiques, des amplificateurs opérationnels et des valeurs de résistance pondérées. Son inconvénient est que les valeurs de résistance de chaque résistance pondérée sont différentes, et lorsqu’il y a beaucoup de chiffres, les valeurs de résistance varient considérablement, ce qui pose de grandes difficultés pour assurer la précision, en particulier pour la production de circuits intégrés. Par conséquent, dans le DAC intégré, ce circuit est rarement utilisé seul.
Indicateurs techniques principaux du DAC
Précision et vitesse de conversion du DAC : La précision de conversion est généralement décrite par la résolution et l’erreur de conversion dans un DAC.
Résolution
Généralement, le nombre de bits du DAC est utilisé pour mesurer la résolution, car plus le nombre de bits est élevé, plus le nombre de valeurs (2n) de la tension de sortie vO est important, et plus il peut refléter les subtiles variations de la tension de sortie. Plus la résolution est élevée.
De plus, la résolution peut également être définie par le rapport de la tension de sortie minimale 1 LSB que le DAC peut distinguer à la tension de sortie maximale FSR. qui est :
résolution=1LSB/FSR=k/k(2n-1)=1/(2n-1)
Plus la valeur est petite, plus la résolution est élevée.
Erreur de conversion
L’erreur de conversion est l’écart maximal entre la tension analogique de sortie réelle et la valeur idéale. Généralement exprimée en pourcentage ou en plusieurs LSB du rapport de cet écart maximal à la FSR. En fait, il s’agit d’un indicateur complet des trois erreurs.
Vitesse de conversion
La vitesse de conversion est généralement déterminée par le temps de stabilisation. Du moment où l’entrée passe de tous les 0 à tous les 1, jusqu’à ce que la tension de sortie se stabilise dans la plage de FSR ± ½ LSB (ou la plage spécifiée par FSR ± x% FSR), cette période est appelée le temps de stabilisation, qui est la réponse maximale du DAC Temps, donc utilisez-le pour mesurer la vitesse de conversion.
Types de DAC
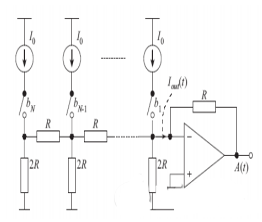
Type résistif
La structure est illustrée à la Figure 1. Ce que montre la Figure 1 est un convertisseur de type réseau échelle R-2R. Son avantage est qu’il peut atteindre une très bonne linéarité. Étant donné que toutes les sources de courant sont équivalentes, nous pouvons utiliser une technologie supplémentaire spéciale pour réduire l’erreur entre elles, et sa structure est beaucoup plus simple que celle d’un diviseur de résistance. L’inconvénient est que la résistance est toujours non linéaire, et elle contient également une capacitance parasite liée au signal, ce qui rend difficile une correspondance parfaite. En même temps, la vitesse est limitée par la mémoire tampon de sortie, et la vitesse ne peut pas être très élevée.
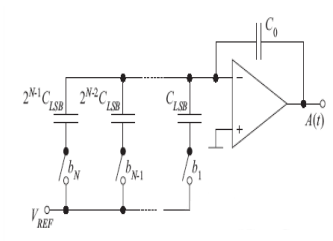
De type capacitif
La structure est illustrée à la Figure 2. La capacitance de l’ordre le plus élevé CN est 1 2N− fois supérieure à celle de la capacitance de l’ordre le plus faible C1. L’avantage est que la consommation d’énergie est faible et que la précision de la correspondance est supérieure à celle de la résistance. Les principaux facteurs limitants sont le désaccord des condensateurs, la résistance à l’état passant des commutateurs, les retards RC importants et l’impact de la bande passante limitée de l’amplificateur sur la vitesse du DAC. Un inconvénient majeur des DAC à distribution de charge est que les condensateurs dans les processus CMOS occupent une grande surface de puce pour être mis en œuvre. Enfin, étant donné que la capacitance dans le processus CMOS est intrinsèquement non linéaire, la linéarité du DAC global sera supprimée. Convient aux applications de haute précision à bande moyenne et large.
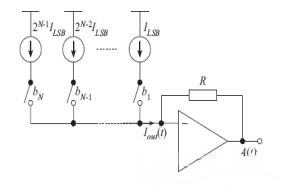
De type courant
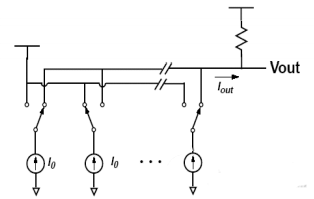
La structure est illustrée à la figure 3. L’avantage est que lorsque la précision est inférieure à 10 bits, la zone peut être rendue très petite, et la vitesse n’est pas limitée par la bande passante de l’amplificateur et le grand délai RC. Elle peut atteindre une vitesse très élevée. Étant donné que tous les courants s’écoulent directement vers la borne de sortie, la consommation d’énergie est très efficace et facile à mettre en œuvre. Les inconvénients sont la sensibilité aux défauts de correspondance des dispositifs et l’impédance de sortie limitée de la source de courant. Convient aux exigences haut débit.
Il est également possible de ne pas utiliser d’amplificateur opérationnel pour la sortie, et d’utiliser directement la résistance de charge pour convertir le courant en une sortie de tension, comme le montre la figure 4. Cette forme permet au débit du DAC de ne pas être limité par la bande passante de l’ampli opérationnel.
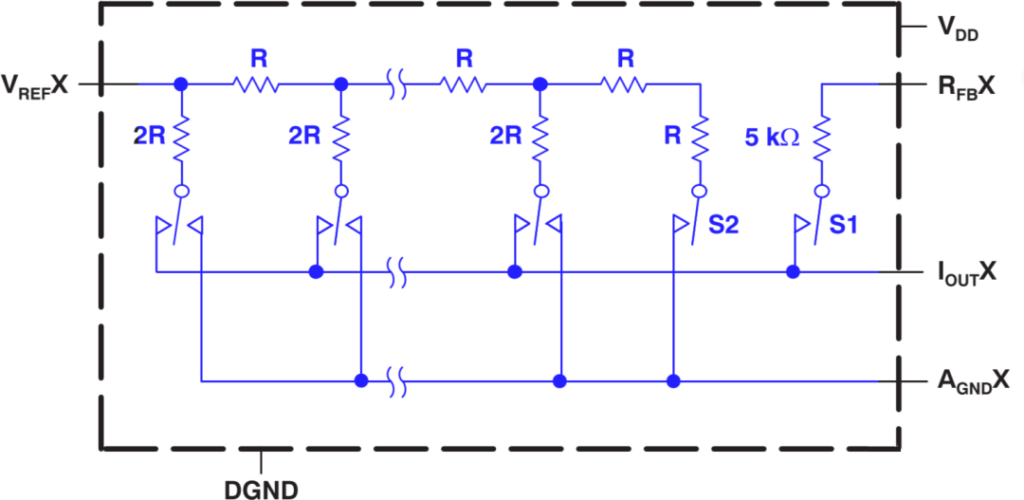
Type multiplicateur
Certains des convertisseurs DA utilisent une tension de référence constante, et d’autres ajoutent un signal AC à l’entrée de tension de référence. Ce dernier est appelé convertisseur DA de type multiplicateur car il peut obtenir le résultat de la multiplication de l’entrée numérique et de l’entrée de tension de référence. En général, un convertisseur DA multiplicateur peut non seulement effectuer une multiplication, mais également être utilisé comme atténuateur pour atténuer numériquement un signal d’entrée et comme modulateur pour moduler un signal d’entrée.
Un convertisseur DA
Par opposition au système de conversion dont nous venons de parler, un convertisseur DA utilise une méthode spéciale pour transformer les valeurs numériques en une modulation de largeur d’impulsion ou une modulation de fréquence, qui est ensuite lissée avec un filtre numérique pour produire une sortie de tension couramment utilisée (également connue sous le nom de mode à flux de bits) pour l’audio, etc.
Conclusion
Le convertisseur ADC et DAC sont deux composants essentiels de tout système numérique. Ils aident à convertir les signaux analogiques en signaux numériques et vice versa. L’ADC (convertisseur analogique-numérique) prend un signal analogique et le convertit en un signal numérique, tandis que le DAC (convertisseur numérique-analogique) prend un signal numérique et le convertit en un signal analogique. Ces deux composants sont importants pour un large éventail d’applications, du traitement audio et vidéo à la transmission de données. Dans cet article, nous avons discuté du fonctionnement de ces convertisseurs et de leur importance dans différentes applications. Nous avons également exploré les différents types de convertisseurs, les différents types de signaux qu’ils peuvent convertir, ainsi que les avantages et les inconvénients de chaque type.