Qu'est-ce que le binaire ?
Le système binaire est un système de numération en base 2 inventé par Gottfried Leibniz, l'un des quatre systèmes de numération. Dans ce système, il est généralement représenté par deux symboles différents, 0 et 1 .

Dans les circuits électroniques numériques, la mise en œuvre des portes logiques utilise directement le système binaire, qui est utilisé dans les ordinateurs modernes et les appareils qui reposent sur les ordinateurs. Chaque nombre est appelé un bit (abréviation de « Binary digit », chiffre binaire).
En logique booléenne, un seul chiffre binaire ne peut représenter que Vrai (1) ou Faux (0), mais plusieurs chiffres binaires peuvent être utilisés pour représenter de grands nombres et effectuer des fonctions complexes. Tout nombre entier peut être représenté en binaire.
Dans la mémoire, le stockage, le traitement et la communication des données numériques, les valeurs 0 et 1 sont parfois appelées respectivement « niveau bas » et « niveau haut ».

Le terme « binaire » peut également être utilisé pour décrire des programmes logiciels compilés. Une fois compilé, un programme contient des données binaires appelées « code machine » qui peuvent être exécutées par le processeur de l'ordinateur.
Qu'est-ce qu'Octal ?
Le système octal, abrégé OCT ou O, est un système de numération basé sur 8. Il utilise les huit chiffres 0, 1, 2, 3, 4, 5, 6, 7, où après 7, il recommence à 0 et incrémente le chiffre supérieur de 1. Dans certains langages de programmation, un chiffre 0 en tête indique souvent que le nombre est en octal. Les nombres octaux et les nombres binaires correspondent bit par bit (un chiffre octal correspond à trois chiffres binaires), ce qui rend l'octal utile dans les langages informatiques.
Le système octal a été largement utilisé dans des systèmes informatiques tels que le PDP-8, l'ICL 1900 et les grands ordinateurs centraux IBM, qui utilisent des mots de 12, 24 ou 36 bits. Ces systèmes sont basés sur le système octal, car leurs mots binaires idéaux sont des multiples de 3 (chaque chiffre octal représente trois chiffres binaires). L'affichage de quatre à douze chiffres représente de manière succincte l'ensemble de la machine. Il permet également de réduire les coûts, car les chiffres peuvent être affichés sur des écrans numériques, des afficheurs à sept segments et des calculatrices pour les panneaux de commande des opérateurs. Les affichages binaires sont trop complexes, les affichages décimaux nécessitent un matériel sophistiqué, tandis que les affichages hexadécimaux exigent l'affichage d'un plus grand nombre de chiffres.
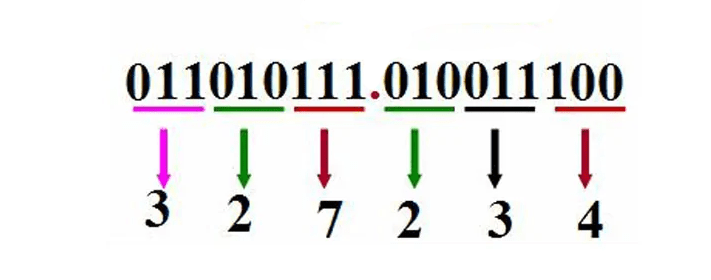
Étant donné qu'un chiffre hexadécimal correspond à quatre chiffres binaires, le système hexadécimal est plus pratique pour représenter le système binaire. Par conséquent, l'utilisation du système octal est moins répandue que celle du système hexadécimal. Certains langages de programmation offrent la possibilité de représenter les nombres à l'aide de la notation octale, et quelques anciennes applications Unix utilisent encore le système octal. Les systèmes informatiques nécessitent des conversions de systèmes numériques en interne, en utilisant le binaire comme base. Les conversions de systèmes numériques entre le binaire, l'octal et le décimal sont effectuées en programmation, et FORTRAN77, axé sur le binaire et le décimal, gère ces conversions.
Cependant, toutes les plateformes informatiques modernes utilisent des systèmes 16, 32 ou 64 bits, les plateformes 64 bits se divisant en outre en octets de 8 bits. Dans ces systèmes, trois chiffres octaux satisfont à chaque exigence d'octet, le chiffre octal le plus significatif représentant deux chiffres binaires (avec +1 pour l'octet suivant, le cas échéant). La représentation de mots de 16 bits en octal nécessite 6 chiffres, mais le chiffre octal le plus significatif ne représente qu'un seul chiffre binaire (0 ou 1). Cette limitation empêche la lisibilité des octets, car ils donnent lieu à des chiffres octaux de 4 bits.
Par conséquent, l'hexadécimal est désormais plus couramment utilisé dans les langages de programmation, car deux chiffres hexadécimaux spécifient entièrement un octet. Les plateformes avec des puissances de deux et des tailles de mot rendent les instructions plus compréhensibles. L'architecture x86 omniprésente en est un exemple, bien que le système octal soit rarement utilisé dans cette architecture. Cependant, le système octal peut être utile pour décrire certains encodages binaires, tels que l'octet ModRM, qui est divisé en 2, 3 et 3 bits.
Qu'est-ce que Decimal ?
Le système décimal, souvent appelé système de base 10, est une méthode de comptage dans laquelle chaque série de dix unités correspond à une unité supérieure. Le premier chiffre a une valeur positionnelle de 10^0, le deuxième chiffre 10^1, le Nème chiffre 10^(N-1). La valeur d'un nombre dans ce système est la somme de chaque chiffre (valeur × poids positionnel).
La méthode de comptage décimal est la plus largement utilisée dans la vie quotidienne. Elle se caractérise par un incrément de dix entre les unités adjacentes, formant la base de la notation décimale. Cela provient probablement du fait que les humains possèdent généralement dix doigts, ce qui a influencé le développement de l'arithmétique utilisant le système décimal. Aristote a observé que les humains utilisent généralement le système décimal en raison de la réalité anatomique d'avoir dix doigts.
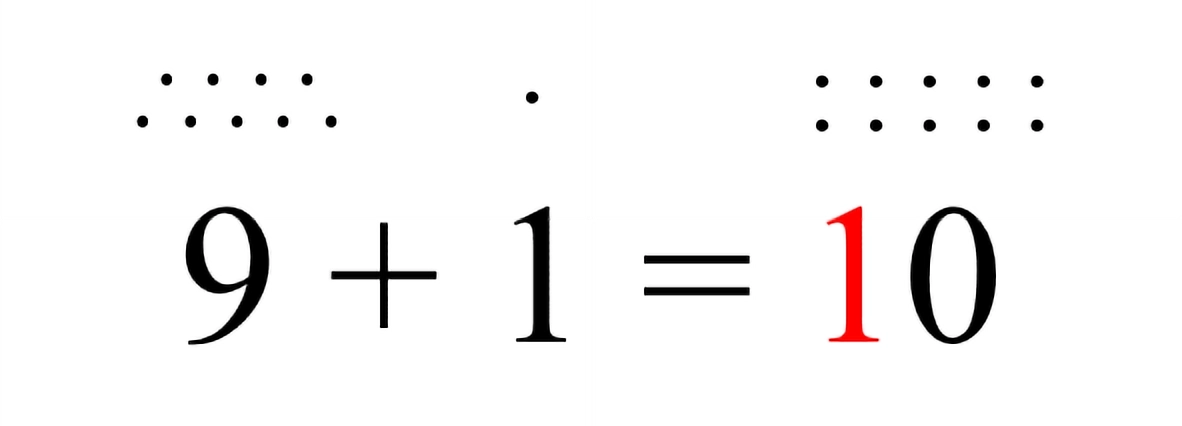
Historiquement, la plupart des systèmes numériques écrits développés indépendamment utilisaient une base décimale, à l'exception des systèmes numériques sexagésimal babylonien (base 60) et vigésimal maya (base 20). Cependant, ces systèmes décimaux n'étaient pas nécessairement positionnels.
Le terme « décimal » vient du mot latin « decem », qui signifie dix. La méthode de comptage décimal a été inventée par des mathématiciens hindous il y a environ 1 500 ans, puis transmise par les Arabes au XIe siècle. Elle repose sur deux principes : la notation positionnelle et la représentation en base dix. Tous les nombres sont composés des dix symboles de base, et lorsqu'une unité atteint dix, elle passe à la position suivante, ce qui rend la position d'un symbole cruciale. Les symboles fondamentaux sont les chiffres de 0 à 9.
Pour représenter les multiples de dix, les chiffres sont décalés d'une position vers la gauche avec un zéro à la fin, ce qui donne 10, 20, 30, etc. De même, les multiples de cent impliquent un nouveau déplacement des chiffres : 100, 200, 300, etc. Pour exprimer une fraction de dix, les chiffres sont déplacés vers la droite et des zéros sont ajoutés si nécessaire : 1/10 devient 0,1, 1/100 devient 0,01 et 1/1000 devient 0,001.
Qu'est-ce que l'hexadécimal ?
L'hexadécimal (abrégé en hex ou indice 16) est un système de numération à base 16, dans lequel chaque 16 est ajouté à 1. Il est généralement représenté par les chiffres 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 et les lettres A, B, C, D, E, F (a, b, c, d, e, f), parmi lesquels A~F représentent 10~15. On les appelle des nombres hexadécimaux.
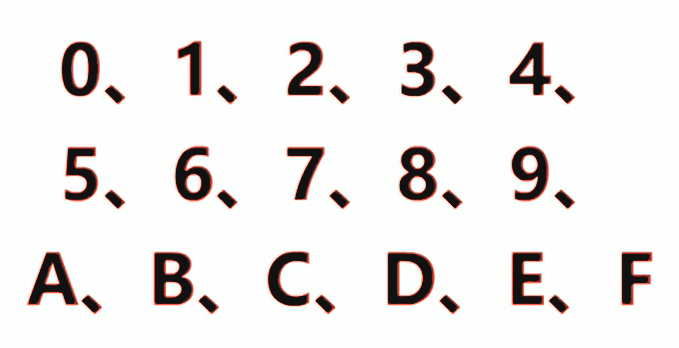
Par exemple, le nombre 57 en décimal s'écrit 111001 en binaire et 39 en hexadécimal. Le système hexadécimal actuel est largement utilisé dans le domaine informatique, car il n'est pas difficile de convertir 4 bits (Bit) en nombres hexadécimaux individuels. 1 octet peut être représenté par 2 nombres hexadécimaux consécutifs. Cependant, cette notation mixte prête à confusion et nécessite l'utilisation de préfixes, de suffixes ou d'indices pour l'afficher.
Décimal en binaire
La conversion d'un nombre décimal en nombre binaire implique des conversions distinctes pour les parties entière et fractionnaire, qui sont ensuite combinées.
Pour la partie entière, on utilise la méthode « diviser par 2 et inverser les restes ». La procédure est la suivante : divisez l'entier décimal par 2, ce qui donne un quotient et un reste. Divisez à nouveau le quotient par 2 et continuez ce processus jusqu'à ce que le quotient soit inférieur à 1. Ensuite, prenez les restes obtenus initialement comme bits les moins significatifs du nombre binaire, et les restes obtenus par la suite comme bits les plus significatifs, en les classant dans l'ordre inverse.
| Decimal | Binary |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
Par exemple, la conversion du nombre décimal 1 en binaire donne 1B (où B signifie le suffixe binaire). Pour le nombre décimal 2, comme nous atteignons 2, nous devons reporter 1, ce qui donne le nombre binaire 10B. De même, lorsque l'on convertit le nombre décimal 5 en binaire, puisque 2 correspond à 10B, alors 3 correspond à 10B + 1B = 11B, 4 correspond à 11B + 1B = 100B et 5 correspond à 100B + 1B = 101B. En poursuivant ce schéma, lorsque le nombre décimal est 254, sa représentation binaire est 11111110B.
Nous pouvons déduire une règle générale pour convertir les nombres binaires en nombres décimaux. En partant du bit le moins significatif du nombre binaire et en remontant, chaque bit représente 2 élevé à la puissance n, où n indique la position du bit à partir de la fin. Ici, n commence à compter à partir de 0. Si un bit binaire a une valeur de 1, il contribue à la somme ; s'il est égal à 0, il n'y contribue pas. Par exemple, inversons le nombre décimal à partir du nombre binaire 11111110B, en suivant le processus de calcul :
0*20+1*21+1*22+1*23+1*24+1*25+1*26+1*27=254
Pourquoi les ordinateurs utilisent-ils le système binaire ?
Tout d'abord, le système binaire n'utilise que deux chiffres, 0 et 1, de sorte que tout élément présentant deux états stables différents peut être utilisé pour représenter un certain bit d'un nombre. En fait, il existe de nombreux composants présentant deux états stables distincts. Par exemple, « allumé » et « éteint » pour une lampe au néon ; « activé » et « désactivé » pour un interrupteur ; « haut » et « bas », « positif » et « négatif » pour une tension ; « aucun trou » ; « signal » et « aucun signal » dans un circuit ; pôles sud et nord des matériaux magnétiques, etc. La liste est longue. Il est facile d'utiliser ces états distincts pour représenter des nombres. De plus, et c'est encore plus important, ces deux états complètement différents ne sont pas seulement quantitativement différents, mais aussi qualitativement différents. De cette manière, la capacité anti-interférence de la machine peut être considérablement améliorée, tout comme sa fiabilité. Il est beaucoup plus difficile de trouver un dispositif simple et fiable capable de représenter plus de deux états.
Deuxièmement, les quatre règles arithmétiques du système de comptage binaire sont très simples. De plus, les quatre opérations arithmétiques peuvent toutes être attribuées à l'addition et au décalage, de sorte que le circuit de l'unité arithmétique dans l'ordinateur électronique est également devenu très simple. Non seulement cela, mais la ligne est simplifiée et la vitesse peut être augmentée. Cela est également incomparable avec le système de comptage décimal.
Troisièmement, l'utilisation de représentations binaires dans les ordinateurs électroniques permet d'économiser du matériel. Il peut être prouvé théoriquement que l'utilisation du système ternaire permet d'économiser le plus de matériel, suivi du système binaire. Cependant, comme le système binaire présente des avantages que les autres systèmes binaires, y compris le système ternaire, n'ont pas, la plupart des ordinateurs électroniques utilisent encore le système binaire. De plus, comme seuls deux symboles « 0 » et « 1 » sont utilisés en binaire, l'algèbre booléenne peut être utilisée pour analyser et synthétiser les circuits logiques de la machine. Cela fournit un outil utile pour la conception de circuits électroniques d'ordinateurs. Quatrièmement, les symboles binaires « 1 » et « 0 » correspondent exactement à « vrai » et « faux » dans les opérations logiques, ce qui est pratique pour les ordinateurs qui effectuent des opérations logiques.
Décimal, binaire et hexadécimal
Le système hexadécimal est similaire au système binaire, à la différence près que le système hexadécimal suit un système « de base seize », dans lequel chaque groupe de seize chiffres est regroupé. Un autre aspect important à noter est que les nombres décimaux de 0 à 15 sont représentés en hexadécimal par 0 à 9, suivis de A, B, C, D, E, F, où 10 en décimal correspond à A en hexadécimal, 11 à B, et ainsi de suite jusqu'à 15 qui correspond à F.
Nous désignons généralement les nombres hexadécimaux en ajoutant le suffixe « H » à la fin, indiquant que le nombre est au format hexadécimal, comme AH, DEH, etc. La casse des lettres n'a pas d'importance ici. Dans le contexte de la programmation en langage C, les nombres hexadécimaux doivent être écrits sous la forme « 0xA » ou « 0xDE », où le préfixe « 0x » signifie hexadécimal.
La conversion entre les nombres décimaux et hexadécimaux n'est pas abordée ici, car les règles sont similaires à celles de la conversion entre les nombres décimaux et binaires. Il est essentiel de maîtriser la conversion entre les nombres décimaux, binaires et hexadécimaux, car ces compétences sont largement utilisées, en particulier dans la programmation de microcontrôleurs en C.
Pour les nombres compris entre 0 et 15, qui sont fréquemment utilisés dans la programmation de microcontrôleurs, la conversion typique consiste d'abord à convertir le binaire en décimal, puis le décimal en hexadécimal. Si vous avez du mal à mémoriser ces conversions pour l'instant, vous pourrez renforcer votre mémoire au fur et à mesure de vos études.
Voici le tableau de conversion des nombres binaires, décimaux et hexadécimaux de 0 à 15 :
| Decimal | Binary | Hexadecimal |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |





