Was ist Binär?
Das Binärsystem ist ein von Gottfried Leibniz erfundenes Zahlensystem zur Basis 2 und eines von vier Zahlensystemen. In diesem System wird es normalerweise durch zwei verschiedene Symbole dargestellt: 0 und 1.

In digitalen elektronischen Schaltungen werden Logikgatter direkt mit Binärzahlen implementiert, die in modernen Computern und computergestützten Geräten verwendet werden. Jede Zahl wird als Bit (Abkürzung für „Binary Digit“) bezeichnet.
In der Booleschen Logik kann eine einzelne Binärziffer nur „wahr“ (1) oder „falsch“ (0) darstellen. Mehrere Binärziffern können jedoch verwendet werden, um große Zahlen darzustellen und komplexe Funktionen auszuführen. Jede ganze Zahl kann in Binärform dargestellt werden.
In der digitalen Datenspeicherung, -verarbeitung und -kommunikation werden die Werte 0 und 1 manchmal als „Low Level” bzw. „High Level” bezeichnet.

Binärcode kann auch zur Beschreibung kompilierter Softwareprogramme verwendet werden. Sobald ein Programm kompiliert ist, enthält es Binärdaten, die als „Maschinencode” bezeichnet werden und von der CPU des Computers ausgeführt werden können.
Was ist Oktal?
Oktal, abgekürzt OCT oder O, ist ein Zahlensystem mit der Basis 8. Es verwendet die acht Ziffern 0, 1, 2, 3, 4, 5, 6, 7, wobei nach 7 wieder bei 0 begonnen wird und die höhere Ziffer um 1 erhöht wird. In einigen Programmiersprachen zeigt eine führende Ziffer 0 oft an, dass es sich um eine Oktalzahl handelt. Oktalzahlen und Binärzahlen entsprechen sich Bit für Bit (eine Oktalziffer entspricht drei Binärziffern), wodurch Oktal in Computersprachen nützlich ist.
Das Oktalsystem wurde häufig in Computersystemen wie PDP-8, ICL 1900 und großen IBM-Mainframes verwendet, die Wortlängen von 12 Bit, 24 Bit oder 36 Bit verwenden. Diese Systeme basieren auf dem Oktalsystem, da ihre idealen Binärwortlängen Vielfache von 3 sind (jede Oktalstelle entspricht drei Binärstellen). Durch die Anzeige von vier bis zwölf Ziffern wird die gesamte Maschine prägnant dargestellt. Außerdem werden die Kosten reduziert, da die Ziffern über Digitalanzeigen, Siebensegmentanzeigen und Taschenrechner für Bedienfelder angezeigt werden können. Binäranzeigen sind zu komplex, Dezimalanzeigen erfordern komplizierte Hardware, während Hexadezimalanzeigen die Anzeige von mehr Ziffern erfordern.
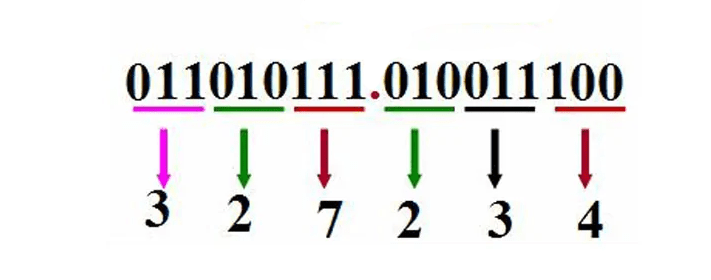
Da eine Hexadezimalziffer vier Binärziffern entspricht, ist Hexadezimal für die Darstellung von Binärzahlen praktischer. Daher ist die Anwendung von Oktal weniger verbreitet als die von Hexadezimal. Einige Programmiersprachen bieten die Möglichkeit, Zahlen in Oktalschreibweise darzustellen, und einige ältere Unix-Anwendungen verwenden noch immer Oktal. Computersysteme erfordern intern Zahlensystemkonvertierungen, wobei Binärzahlen als Basis verwendet werden. Zahlensystemkonvertierungen zwischen Binär-, Oktal- und Dezimalzahlen werden in der Programmierung durchgeführt, und FORTRAN77, das sich auf Binär- und Dezimalzahlen konzentriert, übernimmt diese Konvertierungen.
Alle modernen Computerplattformen verwenden jedoch 16-, 32- oder 64-Bit-Systeme, wobei 64-Bit-Plattformen weiter in 8-Bit-Bytes unterteilt sind. In diesen Systemen erfüllen drei Oktalziffern die Anforderungen jedes Bytes, wobei die höchstwertige Oktalziffer zwei Binärziffern darstellt (mit +1 für das nächste Byte, falls zutreffend). Die Darstellung von 16-Bit-Wörtern in Oktal erfordert 6 Ziffern, aber die höchstwertige Oktalziffer stellt nur 1 Binärziffer (0 oder 1) dar. Diese Einschränkung verhindert leicht lesbare Bytes, da sie zu 4-Bit-Oktalziffern führen.
Infolgedessen wird Hexadezimal heute häufiger in Programmiersprachen verwendet, da zwei Hexadezimalziffern ein Byte vollständig spezifizieren. Plattformen mit Zweierpotenzen und Wortgrößen machen Anweisungen verständlicher. Die allgegenwärtige x86-Architektur ist ein solches Beispiel, obwohl Oktal in dieser Architektur selten verwendet wird. Oktal kann jedoch nützlich sein, um bestimmte Binärkodierungen zu beschreiben, wie z. B. das ModRM-Byte, das in 2, 3 und 3 Bits aufgeteilt ist.
Was ist Dezimal?
Das Dezimalsystem, oft auch als Basis-10-System bezeichnet, ist eine Zählmethode, bei der jeweils zehn Einheiten zu einer höheren Einheit führen. Die erste Ziffer hat einen Positionswert von 10^0, die zweite Ziffer 10^1, die N-te Ziffer 10^(N-1). Der Wert einer Zahl in diesem System ist die Summe der einzelnen Ziffern (Wert × Positionsgewicht).
Die Dezimalzählmethode ist die im Alltag am häufigsten verwendete Zählmethode. Sie zeichnet sich durch eine Steigerung um zehn zwischen benachbarten Einheiten aus und bildet die Grundlage der Dezimalschreibweise. Dies ist wahrscheinlich darauf zurückzuführen, dass Menschen in der Regel zehn Finger haben, was die Entwicklung der Arithmetik unter Verwendung des Dezimalsystems beeinflusst hat. Aristoteles beobachtete, dass Menschen aufgrund der anatomischen Gegebenheit, zehn Finger zu haben, im Allgemeinen das Dezimalsystem verwenden.
Historisch gesehen verwendeten die meisten unabhängig entwickelten schriftlichen Zahlensysteme eine Dezimalbasis, mit Ausnahme des babylonischen Sexagesimalsystems (Basis 60) und des Maya-Vigesimalsystems (Basis 20). Diese Dezimalsysteme waren jedoch nicht unbedingt positionell.
Der Begriff „dezimal” stammt vom lateinischen Wort „decem” ab, was „zehn” bedeutet. Die dezimale Zählweise wurde vor etwa 1.500 Jahren von hinduistischen Mathematikern erfunden und später von den Arabern im 11. Jahrhundert weitergegeben. Sie basiert auf zwei Prinzipien: der Positionsnotation und der Darstellung zur Basis 10. Alle Zahlen setzen sich aus den zehn Grundzeichen zusammen, und wenn eine Einheit zehn erreicht, wird sie auf die nächste Position übertragen, wodurch die Position eines Zeichens entscheidend wird. Die Grundzeichen sind die Ziffern 0 bis 9.
Um Vielfache von zehn darzustellen, werden die Ziffern um eine Position nach links verschoben und mit einer Null ergänzt, was zu 10, 20, 30 usw. führt. In ähnlicher Weise werden bei Vielfachen von hundert die Ziffern erneut verschoben: 100, 200, 300 und so weiter. Um einen Bruchteil von zehn auszudrücken, werden die Ziffern nach rechts verschoben und bei Bedarf Nullen hinzugefügt: 1/10 wird zu 0,1, 1/100 wird zu 0,01 und 1/1000 wird zu 0,001.
Was ist Hexadezimal?
Hexadezimal (abgekürzt als Hex oder Index 16) ist ein Zahlensystem mit der Basis 16, bei dem zu jeder 16 eine 1 hinzugefügt wird. Es wird normalerweise durch die Zahlen 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 und die Buchstaben A, B, C, D, E, F (a, b, c, d, e, f) dargestellt, wobei A bis F die Zahlen 10 bis 15 darstellen. Diese werden als Hexadezimalzahlen bezeichnet.
Beispielsweise wird die Zahl 57 im Dezimalsystem als 111001 im Binärsystem und als 39 im Hexadezimalsystem geschrieben. Das heutige Hexadezimalsystem ist im Computerbereich weit verbreitet, da es nicht schwierig ist, 4 Bits (Bit) in einzelne Hexadezimalzahlen umzuwandeln. 1 Byte kann als 2 aufeinanderfolgende Hexadezimalzahlen dargestellt werden. Diese gemischte Notation ist jedoch verwirrend und erfordert einige Präfixe, Suffixe oder Indizes, um sie darzustellen.
Dezimal zu Binär
Die Umwandlung einer Dezimalzahl in eine Binärzahl umfasst separate Umwandlungen für den ganzzahligen und den gebrochenen Teil, die anschließend kombiniert werden.
Für den ganzzahligen Teil wird die Methode „Durch 2 teilen und die Restzahlen umkehren” verwendet. Das Verfahren läuft wie folgt ab: Teilen Sie die Dezimalganzzahl durch 2, um einen Quotienten und einen Rest zu erhalten. Teilen Sie den Quotienten erneut durch 2 und wiederholen Sie diesen Vorgang, bis der Quotient kleiner als 1 ist. Nehmen Sie dann die ursprünglich erhaltenen Reste als die niedrigstwertigen Bits der Binärzahl und die anschließend erhaltenen Reste als die höchstwertigen Bits und ordnen Sie sie in umgekehrter Reihenfolge an.
| Decimal | Binary |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
Wenn wir zum Beispiel die Dezimalzahl 1 in eine Binärzahl umwandeln, bekommen wir 1B (wobei B für das Binärsuffix steht). Bei der Dezimalzahl 2 müssen wir, weil wir 2 erreichen, 1 übertragen, was zu der Binärzahl 10B führt. Ähnlich verhält es sich bei der Umwandlung der Dezimalzahl 5 in eine Binärzahl: Da 2 gleich 10B ist, ist 3 gleich 10B + 1B = 11B, 4 ist gleich 11B + 1B = 100B und 5 ist gleich 100B + 1B = 101B. Wenn wir dieses Muster fortsetzen, lautet die Binärdarstellung der Dezimalzahl 254 11111110B.
Wir können eine allgemeine Regel für die Umwandlung von Binärzahlen in Dezimalzahlen ableiten. Ausgehend vom niedrigstwertigen Bit der Binärzahl und rückwärtsgehend repräsentiert jedes Bit 2 hoch n, wobei n die Position des Bits vom Ende aus angibt. Hier beginnt n bei 0. Wenn ein Binärbit den Wert 1 hat, trägt es zur Summe bei; wenn es 0 ist, trägt es nicht dazu bei. Lassen Sie uns beispielsweise die Dezimalzahl aus der Binärzahl 11111110B rückwärts berechnen, indem wir dem folgenden Berechnungsprozess folgen:
0*20+1*21+1*22+1*23+1*24+1*25+1*26+1*27=254
Warum verwenden Computer das Binärsystem?
Erstens verwendet das Binärzahlensystem nur zwei Ziffern: 0 und 1. Daher kann jedes Element mit zwei unterschiedlichen stabilen Zuständen verwendet werden, um ein bestimmtes Bit einer Zahl darzustellen. Tatsächlich gibt es viele Komponenten mit zwei unterschiedlichen stabilen Zuständen. Beispiele hierfür sind „ein“ und „aus“ bei einer Neonlampe, „ein“ und „aus“ bei einem Schalter, „hoch“ und „niedrig“, „positiv“ und „negativ“ bei einer Spannung, „kein Loch“, „Signal“ und „kein Signal“ in einem Schaltkreis, Süd- und Nordpol bei magnetischen Materialien usw. Die Liste ließe sich beliebig fortsetzen. Die Verwendung dieser unterschiedlichen Zustände zur Darstellung von Zahlen ist einfach zu implementieren. Darüber hinaus sind die beiden völlig unterschiedlichen Zustände nicht nur quantitativ, sondern auch qualitativ unterschiedlich. Auf diese Weise kann die Störfestigkeit der Maschine erheblich verbessert und die Zuverlässigkeit erhöht werden. Es ist viel schwieriger, ein einfaches und zuverlässiges Gerät zu finden, das mehr als zwei Zustände darstellen kann.
Zweitens sind die vier Rechenregeln des binären Zählsystems sehr einfach. Darüber hinaus lassen sich die vier Rechenoperationen letztendlich alle auf Addition und Verschiebung zurückführen, sodass auch die Schaltung der Recheneinheit im elektronischen Computer sehr einfach geworden ist. Nicht nur das, auch die Leitung wird vereinfacht und die Geschwindigkeit kann erhöht werden. Dies ist ebenfalls mit dem dezimalen Zählsystem nicht zu vergleichen.
Drittens kann die Verwendung von binären Darstellungen in elektronischen Computern Geräte einsparen. Theoretisch lässt sich nachweisen, dass die Verwendung des ternären Systems die meisten Geräte einspart, gefolgt vom binären System. Da das binäre System jedoch Vorteile hat, die andere binäre Systeme, einschließlich des ternären Systems, nicht haben, verwenden die meisten elektronischen Computer immer noch Binärsysteme. Da im Binärsystem nur die beiden Symbole „0” und „1” verwendet werden, kann außerdem die Boolesche Algebra zur Analyse und Synthese der Logikschaltungen in der Maschine verwendet werden. Dies ist ein nützliches Werkzeug für den Entwurf elektronischer Computerschaltungen. Viertens entsprechen die Binärsymbole „1” und „0” genau den Begriffen „wahr” und „falsch” in logischen Operationen, was für Computer die Durchführung logischer Operationen erleichtert.
Dezimal vs. Binär vs. Hexadezimal
Hexadezimal ist ähnlich wie Binär, mit dem wesentlichen Unterschied, dass Hexadezimal einem „Sechzehner-System“ folgt, bei dem jeweils sechzehn Zählwerte zusammengefasst werden. Ein weiterer wichtiger Aspekt ist, dass Dezimalzahlen von 0 bis 15 im Hexadezimalsystem als 0 bis 9 dargestellt werden, gefolgt von A, B, C, D, E, F, wobei 10 im Dezimalsystem A im Hexadezimalsystem entspricht, 11 B und so weiter bis 15, das F entspricht.
Hexadezimalzahlen werden in der Regel durch Hinzufügen des Suffixes „H” am Ende gekennzeichnet, um anzuzeigen, dass es sich um eine Hexadezimalzahl handelt, z. B. AH, DEH usw. Die Groß- und Kleinschreibung spielt dabei keine Rolle. Im Zusammenhang mit der Programmierung in der Sprache C sollten Hexadezimalzahlen als „0xA” oder „0xDE” geschrieben werden, wobei das Präfix „0x” für Hexadezimal steht.
Die Umrechnung zwischen Dezimal- und Hexadezimalzahlen wird hier nicht behandelt, da die Regeln denen der Umrechnung zwischen Dezimal- und Binärzahlen ähneln. Es ist wichtig, die Umrechnung zwischen Dezimal-, Binär- und Hexadezimalzahlen zu beherrschen, da diese Fähigkeiten insbesondere bei der Programmierung von Mikrocontrollern mit C häufig zum Einsatz kommen.
Für Zahlen zwischen 0 und 15, die in der Mikrocontroller-Programmierung häufig verwendet werden, erfolgt die typische Umrechnung zunächst von Binär- in Dezimalzahlen und dann von Dezimal- in Hexadezimalzahlen. Wenn Ihnen diese Umrechnungen derzeit noch schwerfallen, können Sie Ihr Gedächtnis im Laufe Ihres Studiums trainieren.
Hier ist die Umrechnungstabelle für Binär-, Dezimal- und Hexadezimalzahlen von 0 bis 15:
| Decimal | Binary | Hexadecimal |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |