PCB-Design und -Fertigung, Schaltungen und Fertigung

PCB-Leiterbahnbreitenrechner

Willkommen beim PCB-Leiterbahnbreitenrechner! Dieses Tool hilft Ihnen dabei, die optimale Breite einer Kupferleiterbahn für Ihr PCB-Design zu bestimmen, damit diese einen bestimmten Strom sicher leiten kann, ohne den gewünschten Temperaturanstieg zu überschreiten. Durch Eingabe Ihrer Leiterbahnlänge können wir auch wichtige elektrische Parameter wie Widerstand, Spannungsabfall und Leistungsverlust schätzen, die für eine effiziente Schaltungsleistung entscheidend sind.

Bitte beachten Sie, dass diese Ergebnisse auf den Standardformeln der IPC-2221 basieren und Schätzungen sind. Die tatsächliche Leistung kann je nach Ihrer individuellen Anwendung variieren. Für interne Schichten benötigen Sie wahrscheinlich breitere Leiterbahnen als für Oberflächenleiterbahnen. Wählen Sie daher unbedingt die für Ihre Designanforderungen geeignete Berechnung aus.

Internal Layer Results:

Required Trace Width (W):

Resistance:

Voltage Drop:

Power Loss:

External Layer Results:

Required Trace Width (W):

Resistance:

Voltage Drop:

Power Loss:

Den IPC-2221-Standard verstehen

Der IPC-2221 (und seine aktualisierte Version, IPC-2221A) ist der branchenweit anerkannte Standard für das PCB-Design. Er enthält empirische Formeln zur Berechnung der Leiterbahnbreite auf der Grundlage der folgenden Faktoren:

Strombelastbarkeit: Der maximale Strom, den eine Leiterbahn ohne Überhitzung führen kann.
Temperaturanstieg: Der Temperaturanstieg aufgrund des durch die Leiterbahn fließenden Stroms.
Kupferdicke: Dickere Kupferschichten können mehr Strom führen.
Schichttyp: Äußere Schichten leiten Wärme effektiver ab als innere Schichten.

Die Strombelastbarkeit bezieht sich auf den maximalen Strom, den ein Leiter (z. B. eine Leiterbahn auf einer Leiterplatte) sicher führen kann, ohne übermäßige Wärme zu erzeugen oder Schäden zu verursachen. Sie hängt hauptsächlich von den folgenden Faktoren ab:

Leitermaterial: Verschiedene Leitermaterialien haben unterschiedliche spezifische Widerstände. Kupfer ist beispielsweise ein häufig verwendetes Leitermaterial in Leiterplatten, da es einen relativ geringen spezifischen Widerstand hat und somit größere Ströme mit einem kleineren Querschnittsbereich leiten kann.
Querschnittsfläche des Leiters: Je größer die Querschnittsfläche, desto geringer der Widerstand des Leiters und desto größer der Strom, den er leiten kann. Das liegt daran, dass eine größere Querschnittsfläche mehr Wege für den Elektronenfluss bietet, wodurch die Kollision zwischen Elektronen und Atomen verringert und somit der Widerstand gesenkt wird.
Wärmeableitungsbedingungen: Gute Wärmeableitungsbedingungen können die vom Leiter erzeugte Wärme effektiv ableiten und so seine Strombelastbarkeit verbessern. Beispielsweise können bei der Leiterplattenkonstruktion Wärmeableitungsschichten und thermische Durchkontaktierungen hinzugefügt werden, um die Wärmeableitung zu verbessern.

Wenn Strom durch einen Leiter fließt, entsteht aufgrund des Widerstands des Leiters Wärme, wodurch die Temperatur des Leiters ansteigt. Der Temperaturanstieg bezieht sich auf die Erhöhung der Temperatur des Leiters im Verhältnis zur Umgebungstemperatur. Die Höhe des Temperaturanstiegs hängt hauptsächlich von den folgenden Faktoren ab:

Stromstärke: Nach dem Joule'schen Gesetz $Q = I^{2} Rt$ (wobei $Q$ die Wärme, $I$ der Strom, $R$ der Widerstand und $t$ die Zeit ist) gilt: Je größer der Strom, desto mehr Wärme wird erzeugt und desto höher ist der Temperaturanstieg.
Leiterwiderstand: Je höher der Widerstand, desto mehr Wärme wird bei gleichem Strom erzeugt, was zu einem höheren Temperaturanstieg führt.
Wärmeableitungsbedingungen: Gute Wärmeableitungsbedingungen ermöglichen eine schnellere Wärmeableitung und reduzieren so den Temperaturanstieg.

IPC - 2221 Formeln:

Gemäß der Norm IPC-2221 lauten die Schlüsselformeln wie folgt:

Querschnittsfläche:

A = \frac{I}{k \cdot ΔT b}

Variables:

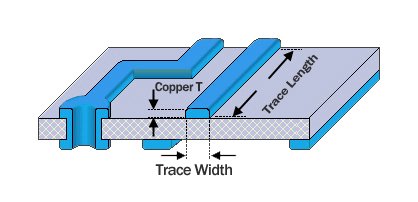
A: Cross-sectional area (mm²)
I: Current (Amperes)
k: Material constant
0.024 for internal layers
0.048 for external layers
ΔT: Temperature rise (°C)
b: Empirical exponent (0.44 for ΔT ≤ 100°C)

Erforderliche Spurbreite (W):

W = \frac{A}{T \cdot 1.378}

Variables:

W:Trace width (mils)
A: Cross-sectional area from Formula 1 (mm²)
T: Copper thickness (oz/ft²)
1.378: Imperial conversion factor

Internal Layer Trace Width:

W = \frac{0.048 \cdot I^{0.44} \cdot T^{0.725}}{{ΔT}^{0.44}}

External Layer Trace Width:

W = \frac{0.024 \cdot I^{0.44} \cdot T^{0.725}}{{ΔT}^{0.44}}

Widerstand:

R = ρ \cdot \frac{L}{T \cdot W} \cdot [1 + α \cdot (t e m p - 25)]

Variables:

R: Trace resistance (Ω)
ρ: Copper resistivity
- 1.72×10⁻⁸ Ω·m (standard)
- 2.44×10⁻⁸ Ω·m @ 100°C
L: Trace length (meters)
T: Copper thickness
- 1 oz/ft² = 0.0347 mm
- 2 oz/ft² = 0.0694 mm
W: Trace width (meters)
α: Temperature coefficient
- 0.00393/°C for copper
- ≈ 3900 ppm/°C
temp: Operating temperature (°C)

Spannungsabfall:

V = I \cdot R = I \cdot \frac{ρ \cdot L}{A}

Variables:

V: Voltage drop (Volts)
I: Current (Amperes)
ρ: Copper resistivity
- 1.72×10⁻⁸ Ω·m @ 20°C
- Temperature adjusted value shown
L: Trace length
- In meters (SI units)
- 1 inch = 0.0254 m

Stromausfall:

P = I^{2} \cdot R

Variables:

P: Power dissipation
- Unit: Watts (W)
- Critical for thermal management
- Max limit determined by PCB material
I: Current
- Unit: Amperes (A)
- RMS value for AC circuits
- Peak value consideration required
R: Trace resistance
- Unit: Ohms (Ω)
- Calculated by: $R = \frac{ρ \cdot L}{T \cdot W}$
- Temperature-dependent property

Umgebungsbedingungen:

W_{adj} = W \cdot {(1 + \frac{RH}{100})}^{0.25}

Variables:

W_adj: Adjusted trace width
W: Base width from Formula 2
RH: Relative humidity (%)
0.25: Environmental factor exponent

Ableitung der IPC-2221-Gleichung

IPC – 2221 ist ein allgemeiner Standard für das Design von Leiterplatten (PCB). Die Formel zur Berechnung der Leiterbahnbreite basiert auf experimentellen Daten und theoretischen Analysen.

Grundprinzip

Die Herleitung dieser Gleichung basiert auf dem Prinzip des thermischen Gleichgewichts des Leiters, d. h. die vom Leiter erzeugte Wärme entspricht der abgegebenen Wärme. Wenn der Leiter das thermische Gleichgewicht erreicht hat, bleibt der Temperaturanstieg stabil.

Ableitungsprozess

Step1: Heat Generation

According to Joule's law, when a current $I$ passes through a conductor with resistance $R$ , the heat generated per unit time $P_{gen}$ is given by the formula:

P_{gen} = I^{2} R

Step2: Heat Dissipation

Heat dissipation mainly occurs through convection and radiation. For PCB traces, convection is the main heat - dissipation method. The power of convective heat dissipation $P_{diss}$ can be expressed as:

P_{diss} = h A Δ T

where $h$ is the convective heat - transfer coefficient, $A$ is the heat - dissipation area of the conductor, and $Δ T$ is the temperature rise.

Step3: Thermal Equilibrium

When thermal equilibrium is reached, the heat generated equals the heat dissipated, so we have:

P_{gen} = P_{diss}

Substituting the expressions for $P_{gen}$ and $P_{diss}$ , we get $I^{2} R = h A Δ T$ .

Resistance Calculation

The resistance of the conductor $R$ is calculated using the formula:

R = ρ \frac{l}{A_{c}}

where $ρ$ is the resistivity of the conductor, $l$ is the length of the conductor, and $A_{c}$ is the cross - sectional area of the conductor.

Step5: Trace Width Calculation

Substituting $R$ into the thermal equilibrium equation and after a series of experimental data fitting and corrections, the formula for calculating the trace width $W$ in IPC - 2221 is obtained.

For internal layer traces:

W = \frac{0.048 \times I^{0.44} \times T^{0.725}}{{Δ T}^{0.44}}

For external layer traces:

W = \frac{0.024 \times I^{0.44} \times T^{0.725}}{{Δ T}^{0.44}}

where $W$ is the trace width (in inches), $I$ is the current (in amperes), $T$ is the copper foil thickness (in ounces per square foot), and $Δ T$ is the temperature rise (in degrees Celsius).

Faktoren, die die Spurbreite beeinflussen

Der Standard IPC-2221 bildet zwar eine solide Grundlage, doch sind noch weitere Faktoren zu berücksichtigen:

Umgebungsbedingungen:

Höhe: In höheren Lagen ist die Luft dünner, wodurch die Wärmeableitung verringert wird.
Gehäuse: Leiterbahnen in geschlossenen Räumen können möglicherweise nicht so effektiv gekühlt werden.
Konforme Beschichtungen: Diese Beschichtungen können die Leiterbahn isolieren und die Wärmeübertragung beeinträchtigen.

Materialeigenschaften:

Widerstandsfähigkeit: Verschiedene Kupferlegierungen haben unterschiedliche elektrische Widerstandsfähigkeiten.
Leiterbahngeometrie: Breite und kurze Leiterbahnen sind effizienter bei der Stromführung.

Designziele:

Signalintegrität: Schmale Leiterbahnen können in Hochfrequenzschaltungen zu Impedanzfehlanpassungen führen.
Stromintegrität: Dicke Leiterbahnen sind unerlässlich, um Spannungsabfälle in Stromversorgungsnetzen zu minimieren.

Wie nutzt man den Rechner effektiv?

Bestimmen Sie Ihre Designanforderungen: Legen Sie den maximalen Strom, den Temperaturanstieg und die Betriebsumgebung fest.
Eingabeparameter: Geben Sie die Werte in den Rechner ein. Verwenden Sie den Modus „Erweitert“ für detaillierte Berechnungen.
Überprüfen Sie die Ergebnisse: Überprüfen Sie die Leiterbahnbreite und die elektrischen Parameter. Passen Sie die Eingaben bei Bedarf an.
Validierung durch Ihren Hersteller: Lassen Sie die Ergebnisse von Ihrem Leiterplattenhersteller bestätigen, um die Herstellbarkeit sicherzustellen.

Häufig gestellte Fragen

F: Kann ich den Rechner für Hochspannungsdesigns verwenden?

A: Ja, aber beachten Sie auch Sicherheitsstandards wie IPC-2221 für Kriechstrecken und Luftstrecken.

F: Was ist, wenn meine Leiterplatte mehrere Schichten hat?

A: Verwenden Sie den Rechner für jede Schicht separat und berücksichtigen Sie dabei die thermischen Eigenschaften jeder einzelnen Schicht.

F: Wie genau sind die Ergebnisse?

A: Der Rechner liefert Schätzwerte. Führen Sie bei kritischen Konstruktionen immer thermische Simulationen durch.

PCB-Reverse-Engineering

PCB-Forward-Engineering

Entwurf und Montage

Test & Fehlerbehebung

Spurbreitenberechnung

PCB-Leiterbahnbreitenrechner

Den IPC-2221-Standard verstehen

IPC - 2221 Formeln: