O que é um circuito RLC?
Um circuito RLC é um circuito elétrico que contém um resistor (R), um indutor (L) e um capacitor (C) conectados em série ou em paralelo. Esses componentes trabalham juntos para armazenar e transferir energia, levando a oscilações em uma frequência ressonante específica. Os circuitos RLC são comumente usados em várias aplicações, incluindo filtros, osciladores e circuitos de sintonia.
Tipos de circuitos RLC
Os circuitos RLC podem ser divididos principalmente nos seguintes tipos:
Circuito da série RLC:
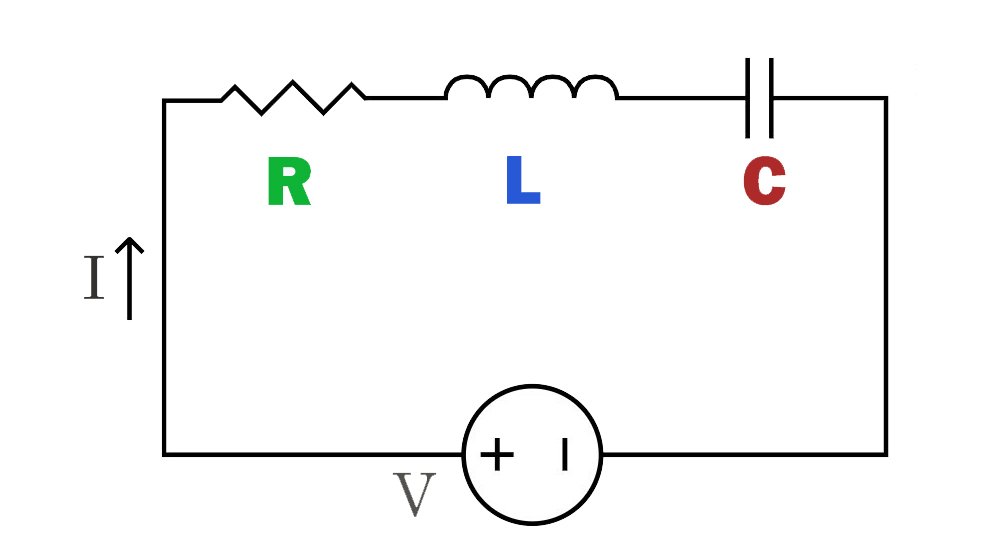
Neste circuito, os componentes resistor (R), indutor (L) e capacitor (C) são conectados em sequência no mesmo caminho. A corrente passa pelo resistor, indutor e capacitor em sequência, fazendo com que a corrente mude de acordo com cada componente.
O circuito RLC em série tem as características de seletividade de frequência, apresentando diferentes características de impedância e resposta em diferentes frequências, por isso é amplamente utilizado em filtros e circuitos sintonizados.
Circuito paralelo RLC:
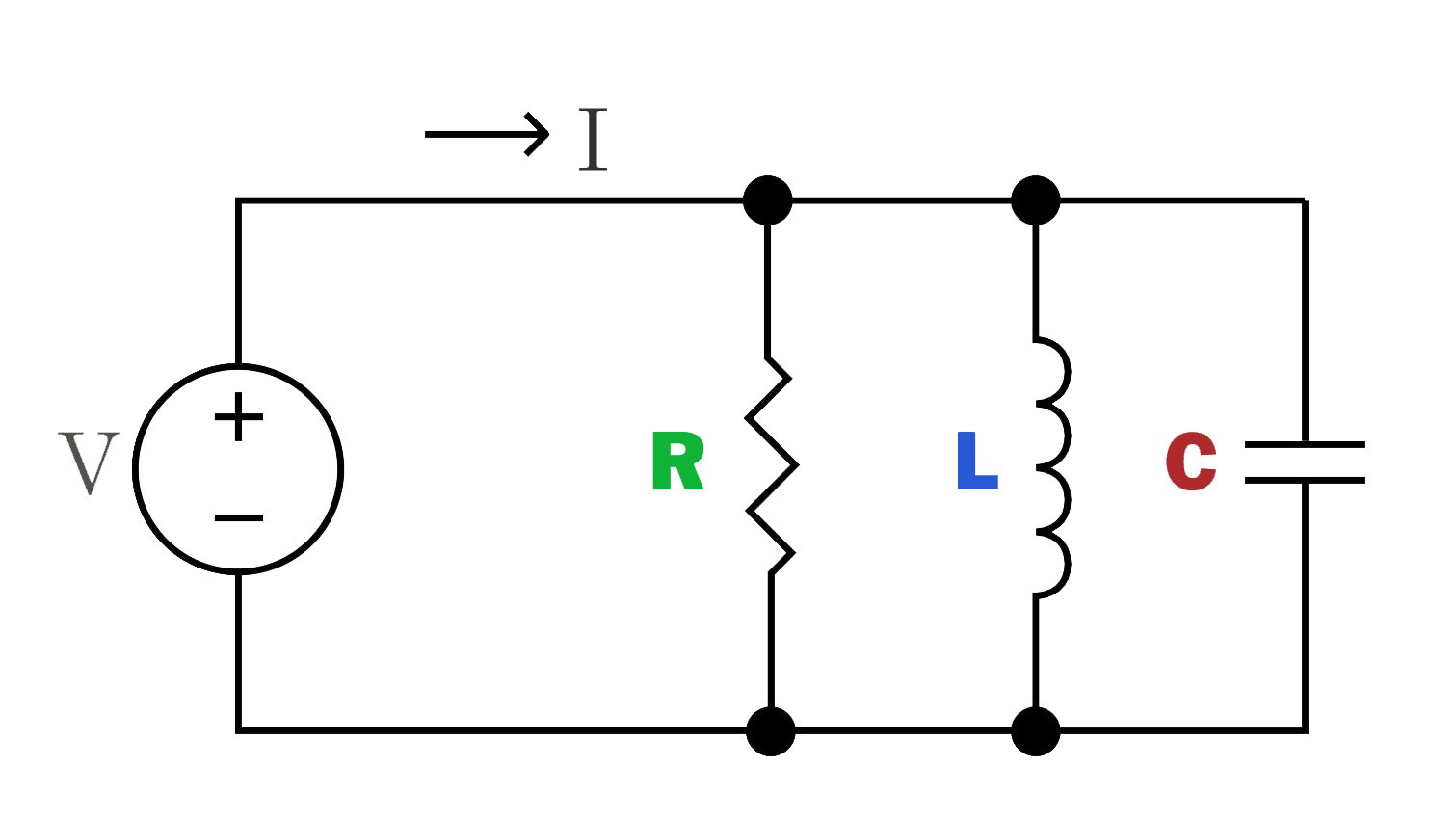
O circuito RLC paralelo consiste em conectar o resistor, o indutor e o capacitor em caminhos paralelos, respectivamente. A corrente é dividida nos ramos, e a tensão que passa por cada componente é a mesma.
O circuito tem características de impedância para corrente em uma frequência específica, que podem ser usadas para passar ou bloquear seletivamente sinais de determinadas frequências.
Como medir a tensão no circuito RLC?
Como mostram os diagramas abaixo:
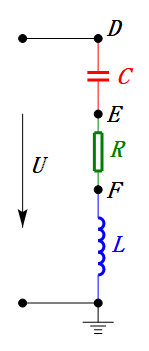
Quando U é uma tensão sinusoidal, este circuito tem três pontos potenciais D, E e F. Estas três formas de onda podem ser observadas utilizando um osciloscópio ou medidas com um voltímetro CA para UD, UE, UL, UR e UC. O gráfico dinâmico à direita reflete as mudanças nessas cinco tensões ao longo do tempo em um determinado cenário. No gráfico dinâmico, UF é equivalente a UL e, idealmente, deveria haver outra tensão UDF, mas optei por não incluir tensões com subscritos de duas letras para simplificar.
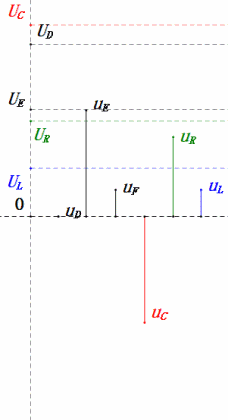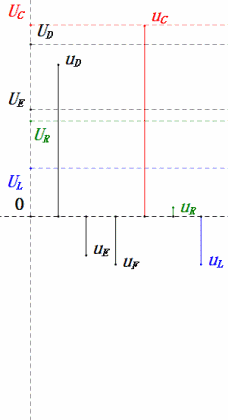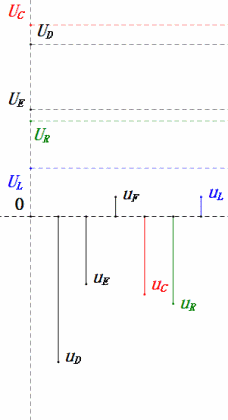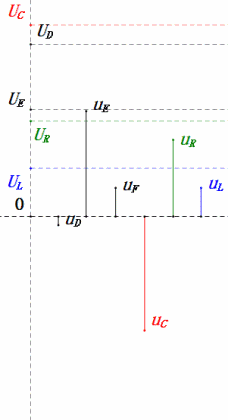
Fórmula de cálculo para tensão
O método fasorial é uma solução brilhante que facilita a resolução de problemas, mas pode fazer com que percamos os fascinantes processos dinâmicos representados no gráfico acima. Com a reatância indutiva XL, a resistência R e a reatância capacitiva XC, o método fasorial para resolver este circuito é descrito da seguinte forma:
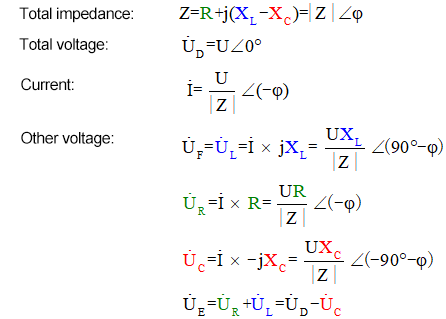
O voltímetro CA mede UR ≠ UE – UL. Se L for um indutor ideal, esses três formarão um triângulo retângulo. Da mesma forma, UC, UD e UE também formarão um triângulo, embora não necessariamente um triângulo retângulo. Isso não significa que a Lei de Kirchhoff (KVL) seja violada. Se o valor instantâneo u em um determinado momento for medido, verificará-se que uR = uE – uL e uC = uD – uE. Além disso, embora a corrente não seja medida, as mudanças em UR estão em fase com as mudanças na corrente.
Ação do sinal senoidal e estado de ressonância
Quando um sinal senoidal é aplicado, a reatância indutiva XL = ωL e a reatância capacitiva XC = (ωC)^-1. O estado em que estas duas são iguais é conhecido como ressonância, permitindo-nos calcular uma frequência angular ressonante ω0.
Na próxima seção, definiremos os parâmetros para criar diagramas fasoriais, diagramas de onda senoidal estática e animações das mudanças instantâneas do valor da tensão em 0,5ω0, ω0 e 2ω0.
Tensão sob diferentes frequências angulares ressonantes
Parâmetros do modelo:
- U = 6,00 mV
- R = 2,00 Ω (corrente efetiva inferior a 3,00 mA, geralmente segura para componentes)
- C = 125μF
- L = 0,500 mH
ω0 calculado = 4000rad/s (correspondente a uma frequência de aproximadamente 637Hz, ignorando os efeitos da radiação eletromagnética para facilitar a modelagem. Os diagramas fasoriais e os diagramas de ondas senoidais utilizam valores RMS; para valores de pico, multiplique por 1,414)
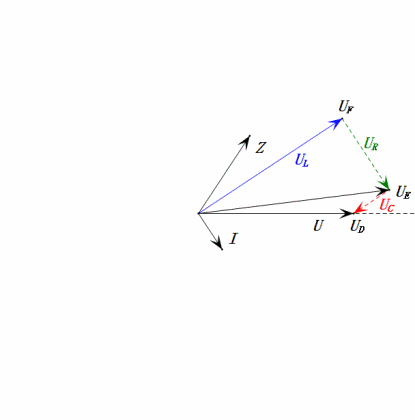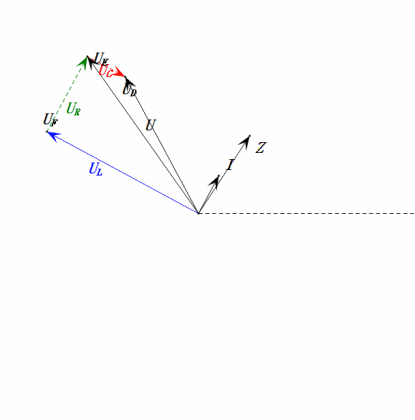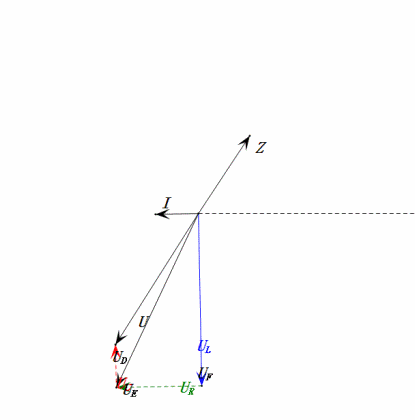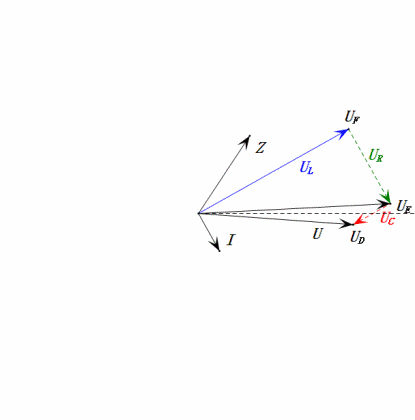
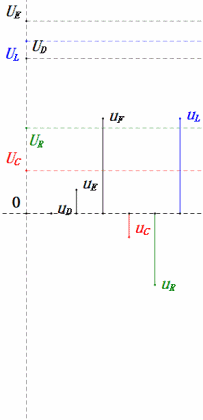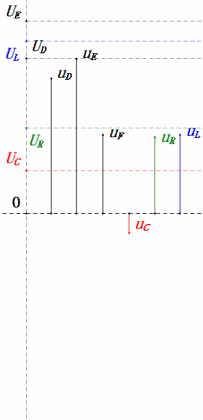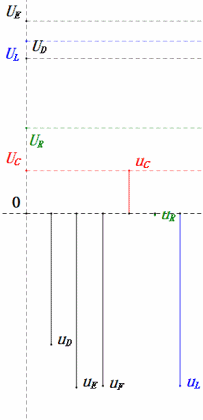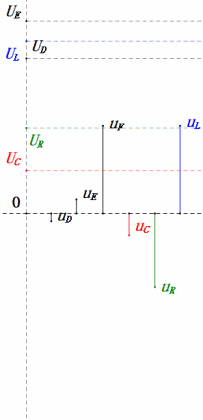
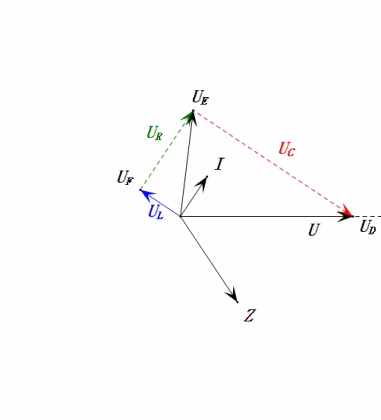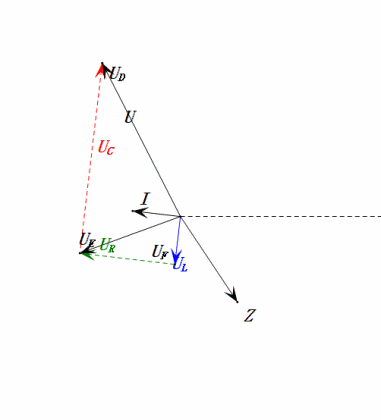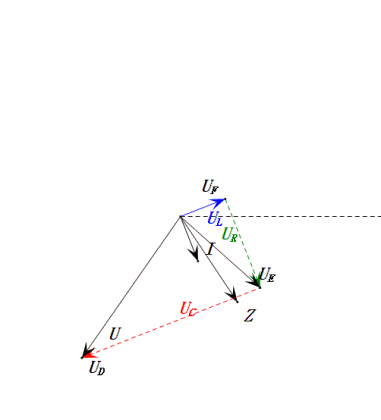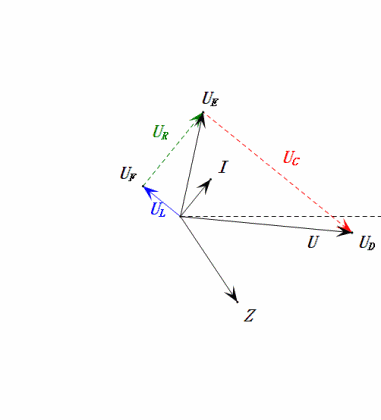
Tensão dinâmica abaixo de 0,5ω0
Após os cálculos, podemos desenhar o diagrama fasorial e o diagrama de onda senoidal estática no momento inicial:
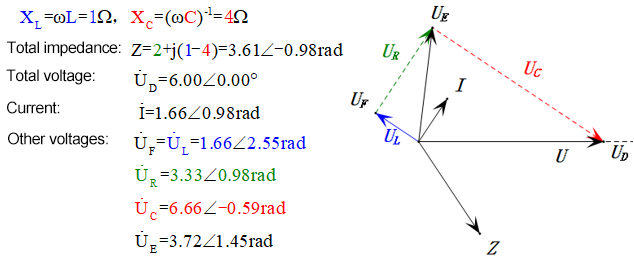
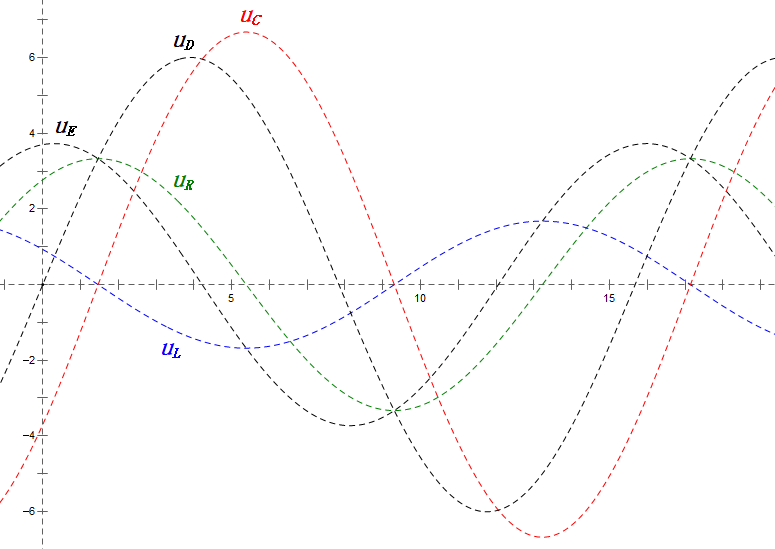
Análise:
- Corrente máxima ≈ 1,57 mA, segura para os componentes.
- O diagrama fasorial forma um trapézio reto sem considerar o UDF.
- Em 0,5ω0, XL < XC → UL menor, UC maior. O uC máximo excede a tensão da fonte de alimentação, podendo danificar o capacitor.
- uC fica ≈30° atrás de uD; o carregamento começa durante a fase ascendente de uD, terminando quando uR = 0.
- O diagrama de onda senoidal mostra uR = uE – uL e uC = uD – uE em todos os momentos.
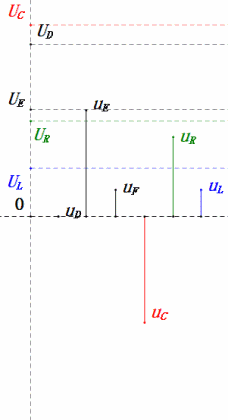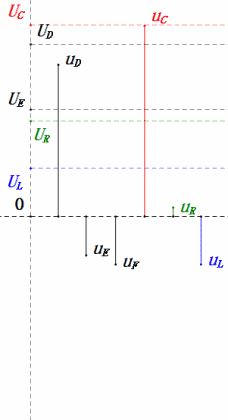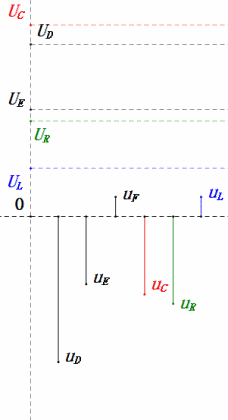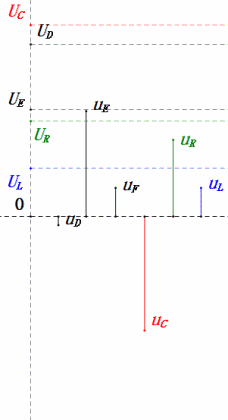
Tensão dinâmica abaixo de 1ω0
Após os cálculos, podemos desenhar o diagrama fasorial e o diagrama de onda senoidal estática no momento inicial:
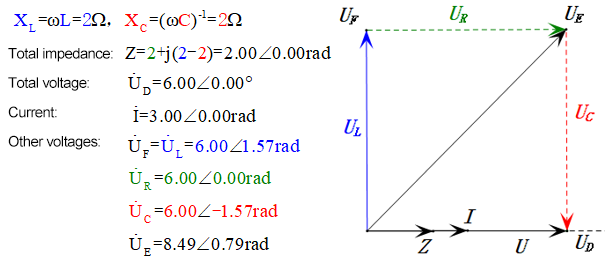
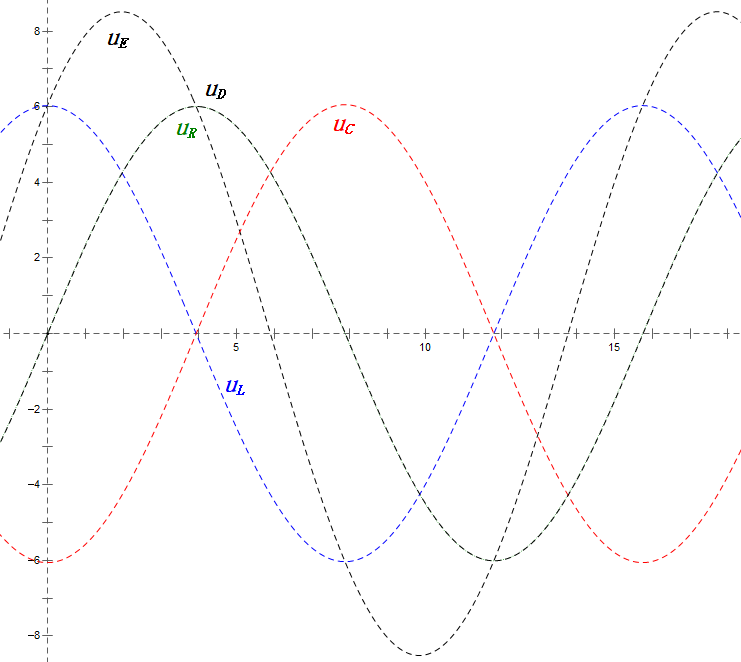
Análise:
- Corrente máxima ≈ 4,24 mA, segura para os componentes.
- O diagrama fasorial forma um quadrado na ressonância (XL = XC).
- O uE máximo excede a tensão da fonte de alimentação, mas o impacto nos componentes não é claro.
- Coincidência: XL = XC = R → uL e uC cancelam-se mutuamente no diagrama de onda senoidal, mas as alterações de corrente afetam as amplitudes.
- Impedância minimizada, corrente maximizada na ressonância devido ao efeito de "corrente máxima".
- uC fica exatamente 90° atrás de uD; o carregamento começa quando uD atinge o pico e termina quando uR = uD = 0.
- Os segmentos do diagrama de onda senoidal representam metade do tempo do Caso 1.
- UD = UR, UL = UC máximos devido aos parâmetros, mas as quatro tensões iguais são uma coincidência.
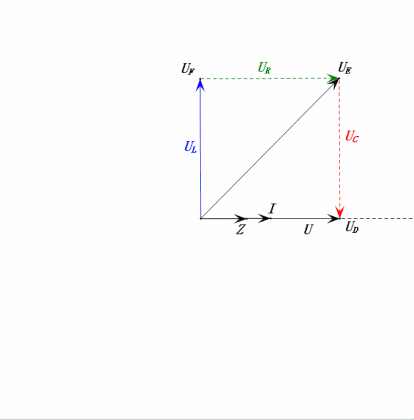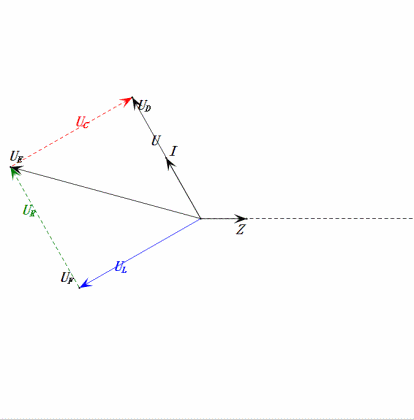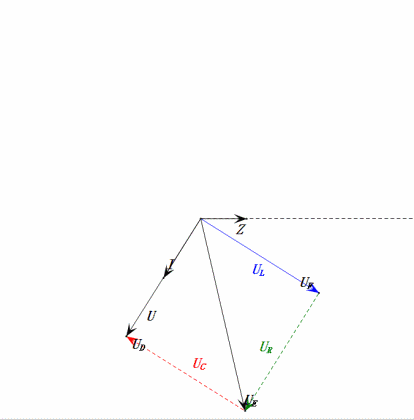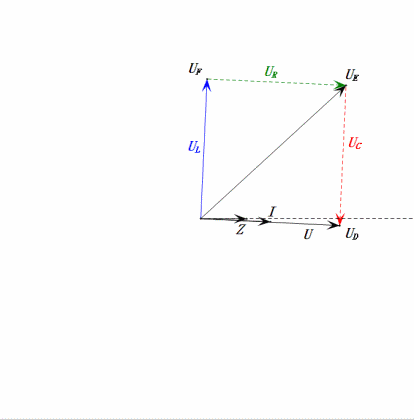
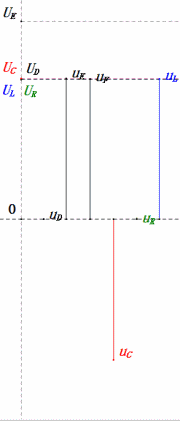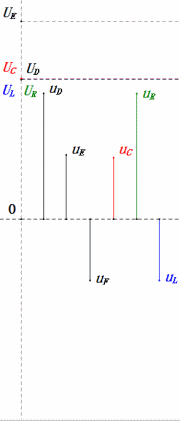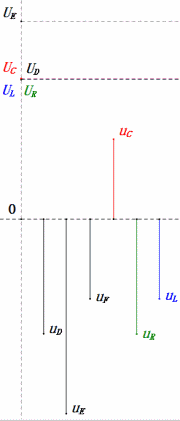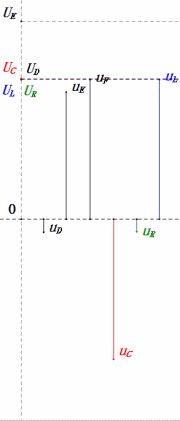
Tensão dinâmica sob 2ω0
Após os cálculos, podemos desenhar o diagrama fasorial e o diagrama de onda senoidal estática no momento inicial:
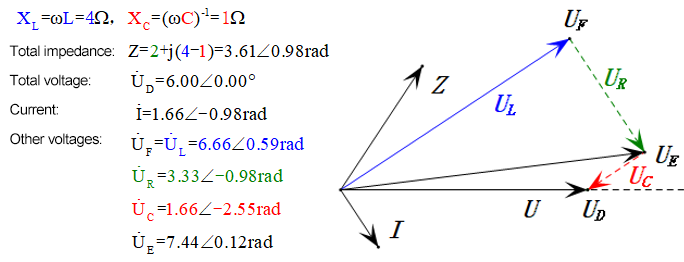
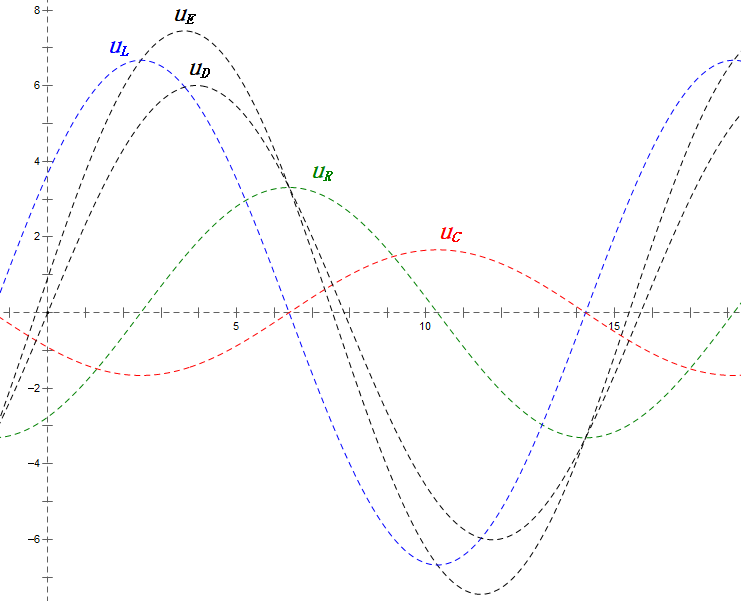
Análise:
- Corrente máxima ≈ 1,57 mA, segura para os componentes.
- O diagrama fasorial forma um trapézio reto.
- Em 2ω0, XL > XC → UL maior, UC menor. uL e uE máximos excedem a tensão da fonte de alimentação, aumentando as preocupações com danos ao indutor.
- uC fica atrás de uD em ≈150°; o carregamento começa quando uD cai para ≈metade do seu máximo, terminando quando uR = uD = 0.
- Os segmentos do diagrama de onda senoidal representam metade do tempo do Caso 2.
- As equações uR = uE – uL e uC = uD – uE são válidas em todos os momentos.