O que é binário?
O binário é um sistema numérico de base 2 inventado por Gottfried Leibniz, um dos quatro sistemas numéricos. Neste sistema, é normalmente representado por dois símbolos diferentes, 0 e 1 .

Nos circuitos eletrônicos digitais, a implementação de portas lógicas utiliza diretamente o sistema binário, que é usado em computadores modernos e dispositivos que dependem de computadores. Cada número é chamado de bit (abreviação de Binary digit, ou dígito binário).
Na lógica booleana, um único dígito binário só pode representar Verdadeiro (1) ou Falso (0); no entanto, vários dígitos binários podem ser usados para representar números grandes e executar funções complexas, qualquer número inteiro pode ser representado em binário.
Na memória, armazenamento, processamento e comunicação de dados digitais, os valores 0 e 1 são às vezes chamados de "nível baixo" e "nível alto", respectivamente.

O binário também pode ser usado para descrever programas de software compilados. Depois que um programa é compilado, ele contém dados binários chamados "código de máquina", que podem ser executados pela CPU do computador.
O que é Octal?
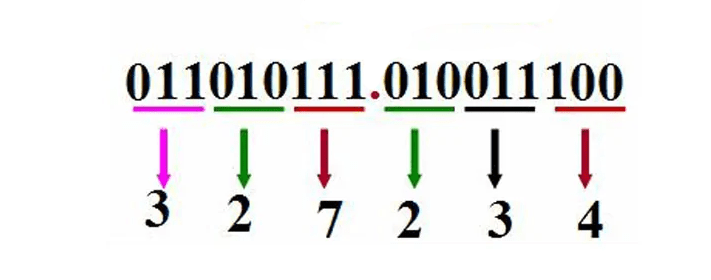
O octal, abreviado como OCT ou O, é um sistema de contagem com base 8. Ele emprega os oito dígitos 0, 1, 2, 3, 4, 5, 6, 7, onde após o 7 ele volta para 0 e incrementa o dígito superior em 1. Em algumas linguagens de programação, um dígito inicial 0 geralmente indica que o número está em octal. Os números octais e binários correspondem-se bit a bit (um dígito octal corresponde a três dígitos binários), tornando o octal útil em linguagens de computador.
O octal tem sido amplamente utilizado em sistemas de computador como PDP-8, ICL 1900 e grandes mainframes IBM, que utilizam comprimentos de palavra de 12 bits, 24 bits ou 36 bits. Esses sistemas são baseados no octal, uma vez que seus comprimentos de palavra binários ideais são múltiplos de 3 (cada dígito octal representa três dígitos binários). A exibição de quatro a doze dígitos representa sucintamente toda a máquina. Isso também reduz custos, pois os dígitos podem ser exibidos em displays digitais, displays de sete segmentos e calculadoras para painéis de controle do operador. Os displays binários são muito complexos e os displays decimais requerem hardware complexo, enquanto os displays hexadecimais exigem a exibição de mais dígitos.
Como um dígito hexadecimal corresponde a quatro dígitos binários, o hexadecimal é mais conveniente para representar o binário. Portanto, a aplicação do octal é menos difundida do que a do hexadecimal. Algumas linguagens de programação oferecem a capacidade de representar números usando a notação octal, e alguns aplicativos Unix mais antigos ainda usam o octal. Os sistemas de computador exigem conversões internas do sistema numérico, usando o binário como base. As conversões do sistema numérico entre binário, octal e decimal são realizadas na programação, e o FORTRAN77, focado no binário e no decimal, lida com essas conversões.
No entanto, todas as plataformas de computação modernas usam sistemas de 16, 32 ou 64 bits, onde as plataformas de 64 bits se dividem ainda mais em bytes de 8 bits. Nesses sistemas, três dígitos octais satisfazem cada requisito de byte, com o dígito octal mais significativo representando dois dígitos binários (com +1 para o próximo byte, se aplicável). Representar palavras de 16 bits em octal requer 6 dígitos, mas o dígito octal mais significativo representa apenas 1 dígito binário (0 ou 1). Essa limitação impede bytes fáceis de ler, pois resultam em dígitos octais de 4 bits.
Como resultado, o hexadecimal é agora mais comumente usado em linguagens de programação, pois dois dígitos hexadecimais especificam totalmente um byte. Plataformas com potências de dois e tamanhos de palavra tornam as instruções mais compreensíveis. A arquitetura x86 onipresente é um exemplo disso, embora o octal raramente seja usado nessa arquitetura. No entanto, o octal pode ser útil para descrever certas codificações binárias, como o byte ModRM, que é dividido em 2, 3 e 3 bits.
O que é decimal?
O sistema decimal, frequentemente referido como sistema de base 10, é um método de contagem em que cada dez unidades conduzem a uma unidade superior. O primeiro dígito tem um valor posicional de 10^0, o segundo dígito 10^1, o N-ésimo dígito 10^(N-1). O valor de um número neste sistema é a soma de cada dígito (valor × peso posicional).
O método de contagem decimal é o mais utilizado na vida cotidiana. Ele apresenta um incremento de dez entre unidades adjacentes, formando a base da notação decimal. Isso provavelmente decorre do fato de que os seres humanos normalmente possuem dez dedos, influenciando o desenvolvimento da aritmética usando o sistema decimal. Aristóteles observou que os seres humanos geralmente usam o sistema decimal devido à realidade anatômica de ter dez dedos.
Historicamente, a maioria dos sistemas numéricos escritos desenvolvidos de forma independente empregava uma base decimal, exceto os sistemas numéricos sexagesimal babilônico (base 60) e vigesimal maia (base 20). No entanto, esses sistemas decimais não eram necessariamente posicionais.
O termo "decimal" tem origem na palavra latina "decem", que significa dez. O método de contagem decimal foi inventado por matemáticos hindus há cerca de 1.500 anos e posteriormente transmitido pelos árabes no século XI. Baseia-se em dois princípios: notação posicional e representação na base dez. Todos os números são compostos pelos dez símbolos básicos e, quando uma unidade atinge dez, ela é transferida para a próxima posição, tornando a posição de um símbolo crucial. Os símbolos fundamentais são os dígitos de 0 a 9.
Para representar múltiplos de dez, os dígitos são deslocados uma posição para a esquerda com um zero à direita, resultando em 10, 20, 30 e assim por diante. Da mesma forma, os múltiplos de cem envolvem o deslocamento dos dígitos novamente: 100, 200, 300 e assim por diante. Para expressar uma fração de dez, os dígitos são deslocados para a direita e zeros são adicionados conforme necessário: 1/10 torna-se 0,1, 1/100 torna-se 0,01 e 1/1000 torna-se 0,001.
O que é hexadecimal?
Hexadecimal (abreviado como hex ou subscrito 16) é um sistema de contagem com base 16, no qual cada 16 é adicionado a 1. Normalmente representado pelos números 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 e pelas letras A, B, C, D, E, F (a, b, c, d, e, f), entre os quais: A~F representam 10~15, estes são chamados números hexadecimais.
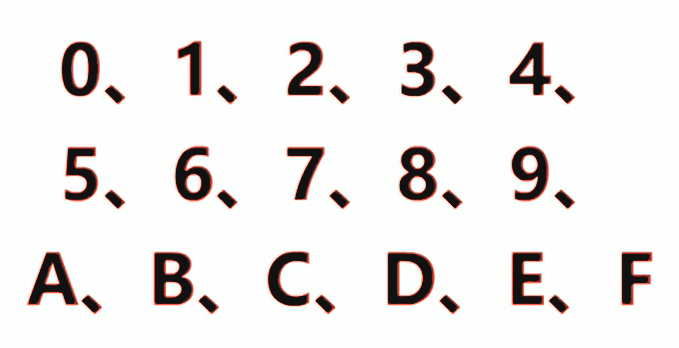
Por exemplo, o número 57 em decimal é escrito como 111001 em binário e 39 em hexadecimal. O sistema hexadecimal atual é amplamente utilizado na área da informática, pois não é difícil converter 4 bits (Bit) em números hexadecimais individuais. 1 byte pode ser representado como 2 números hexadecimais consecutivos. No entanto, essa notação mista é confusa e requer alguns prefixos, sufixos ou subscritos para ser representada.
Decimal para binário
A conversão de um número decimal em um número binário envolve conversões separadas para as partes inteira e fracionária, que são então combinadas.
Para a parte inteira, é utilizado o método "dividir por 2 e inverter os restos". O procedimento é o seguinte: Divida o inteiro decimal por 2, obtendo um quociente e um resto. Divida o quociente por 2 novamente e continue esse processo até que o quociente seja menor que 1. Em seguida, considere os restos obtidos inicialmente como os bits menos significativos do número binário e os restos obtidos posteriormente como os bits mais significativos, organizando-os na ordem inversa.
| Decimal | Binary |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
Por exemplo, converter o número decimal 1 para binário resulta em 1B (onde B significa o sufixo binário). Para o número decimal 2, como chegamos a 2, precisamos transportar 1, resultando no número binário 10B. Da mesma forma, ao converter o número decimal 5 para binário, como 2 é 10B, então 3 é 10B + 1B = 11B, 4 é 11B + 1B = 100B e 5 é 100B + 1B = 101B. Continuando esse padrão, quando o número decimal é 254, sua representação binária é 11111110B.
Podemos deduzir uma regra geral ao converter números binários em números decimais. Começando pelo bit menos significativo do número binário e retrocedendo, cada bit representa 2 elevado à potência de n, onde n indica a posição do bit a partir do final. Aqui, n começa a contar a partir de 0. Se um bit binário tem um valor de 1, ele contribui para a soma; se for 0, ele não contribui. Por exemplo, vamos fazer a engenharia reversa do número decimal a partir do número binário 11111110B, seguindo o processo de cálculo:
0*20+1*21+1*22+1*23+1*24+1*25+1*26+1*27=254
Por que os computadores usam o sistema binário?
Primeiro, o sistema numérico binário usa apenas dois dígitos: 0 e 1. Assim, qualquer elemento com dois estados estáveis diferentes pode ser usado para representar um determinado bit de um número. Na verdade, existem muitos componentes com dois estados estáveis distintos. Por exemplo, "ligado" e "desligado" de uma lâmpada de néon; "ligado" e "desligado" de um interruptor; "alto" e "baixo", "positivo" e "negativo" de uma tensão; "Sem falha"; "sinal" e "sem sinal" no circuito; pólos sul e norte de materiais magnéticos, etc., e a lista continua. Usar esses estados distintos para representar números é fácil de implementar. Além disso, o mais importante é que os dois estados completamente diferentes não são apenas quantitativamente diferentes, mas também qualitativamente diferentes. Dessa forma, a capacidade anti-interferência da máquina pode ser bastante aprimorada e a confiabilidade pode ser melhorada. É muito mais difícil encontrar um dispositivo simples e confiável que possa representar mais de dois estados.
Em segundo lugar, as quatro regras aritméticas do sistema de contagem binário são muito simples. Além disso, as quatro operações aritméticas podem ser atribuídas à adição e ao deslocamento no final, de modo que o circuito da unidade aritmética no computador eletrônico também se tornou muito simples. Além disso, a linha é simplificada e a velocidade pode ser aumentada. Isso também é incomparável ao sistema de contagem decimal.
Em terceiro lugar, o uso de representações binárias em computadores eletrônicos pode economizar equipamentos. Pode-se provar teoricamente que o uso do sistema ternário economiza mais equipamentos, seguido pelo sistema binário. No entanto, como o sistema binário tem vantagens que outros sistemas binários, incluindo o sistema ternário, não têm, a maioria dos computadores eletrônicos ainda usa o binário. Além disso, como apenas dois símbolos "0" e "1" são usados no binário, a álgebra booleana pode ser usada para analisar e sintetizar os circuitos lógicos na máquina. Isso fornece uma ferramenta útil para projetar circuitos de computadores eletrônicos. Quarto, os símbolos binários "1" e "0" correspondem exatamente a "verdadeiro" e "falso" em operações lógicas, o que é conveniente para os computadores realizarem operações lógicas.
Decimal vs. Binário vs. Hexadecimal
O hexadecimal é semelhante ao binário, com a diferença fundamental de que o hexadecimal segue um sistema de "base dezesseis", em que cada dezesseis contagens são agrupadas. Outro aspecto importante a ser observado é que os números decimais de 0 a 15 são representados em hexadecimal como 0 a 9, seguidos por A, B, C, D, E, F, onde 10 em decimal corresponde a A em hexadecimal, 11 a B e assim por diante até 15, que corresponde a F.
Geralmente, denotamos números hexadecimais adicionando o sufixo "H" ao final, indicando que o número está no formato hexadecimal, como AH, DEH, etc. O uso de letras maiúsculas ou minúsculas não é significativo aqui. No contexto da programação na linguagem C, os números hexadecimais devem ser escritos como "0xA" ou "0xDE", onde o prefixo "0x" significa hexadecimal.
A conversão entre números decimais e hexadecimais não é discutida aqui, pois as regras são semelhantes à conversão entre decimal e binário. É fundamental ser proficiente na conversão entre números decimais, binários e hexadecimais, pois essas habilidades são amplamente utilizadas, especialmente na programação de microcontroladores usando C.
Para números entre 0 e 15, que são frequentemente usados na programação de microcontroladores, a conversão típica envolve primeiro converter binário para decimal e, em seguida, decimal para hexadecimal. Se você achar difícil lembrar essas conversões agora, pode reforçar sua memória à medida que avança nos estudos.
Aqui está a tabela de conversão para números binários, decimais e hexadecimais de 0 a 15:
| Decimal | Binary | Hexadecimal |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |





