I cancelli logici sono i componenti di base dei circuiti integrati. Semplici cancelli logici possono essere realizzati con transistor. La combinazione di questi transistor può far passare i livelli alto e basso che rappresentano i due segnali attraverso di essi per generare un segnale di livello alto o basso. I livelli alto e basso possono rispettivamente rappresentare il logico “vero” e “falso” o 1 e 0 in binario, realizzando così operazioni logiche. Per approfondire uno di questi componenti fondamentali, scopri i transistor PMOS.
Cancelli logici di base
Qui introdurremo 7 cancelli logici di base: cancello AND, cancello OR, cancello NOT, cancello NAND, cancello NOR, cancello XOR e cancello XNOR. Imparerai i loro simboli logici, le relazioni logiche e le tabelle di verità.
Cancello AND
Il cancello AND è anche chiamato “circuito AND”, circuito logico “AND”. È un circuito cancello logico di base che esegue l’operazione “AND”. Ci sono più ingressi e una uscita.
L’uscita è alta quando tutti gli ingressi sono alti (logica 1) contemporaneamente, altrimenti l’uscita è bassa (logica 0).
L’espressione logica matematica del cancello AND: Y = AB, la tabella di verità è la seguente:

| Input | Output | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Cancello OR
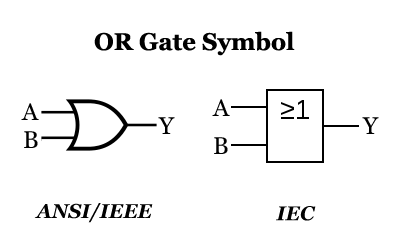
Il cancello OR, noto anche come circuito OR, circuito logico e circuito. Se una delle diverse condizioni è soddisfatta, si verificherà un evento. Questa relazione è chiamata relazione logica “o”. Un circuito con una relazione logica “o” è chiamato cancello OR.
Il cancello OR ha più ingressi e una uscita, finché uno degli ingressi è alto (logica “1”), l’uscita è alta (logica “1”). L’uscita è bassa (logica “0”) solo quando tutti gli ingressi sono bassi (logica “0”).
L’espressione logica matematica del cancello OR è: Y=A+B=(A’B’)’ e i suoi simboli logici e la tabella di verità sono i seguenti:
| Input | Output | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Cancello NOT
Un cancello NOT, noto anche come circuito NOT, inverter o circuito di negazione logica, è l’unità di base di un circuito logico. Un cancello NOT ha un ingresso e una uscita.
Quando l’ingresso è alto (logica “1”), l’uscita è bassa (logica “0”); al contrario, quando l’ingresso è basso (logica “0”), l’uscita è alta (logica “1”). La funzione logica del cancello NOT è equivalente al NOT nell’algebra logica e la funzione del circuito è equivalente all’inversione. Questa operazione è chiamata anche operazione NOT.
L’espressione logica matematica del cancello NOT è: F=A, e i suoi simboli logici e la tabella di verità sono i seguenti:

| Input | Output |
|---|---|
| A | Y |
| 0 | 1 |
| 1 | 0 |
Cancello NAND
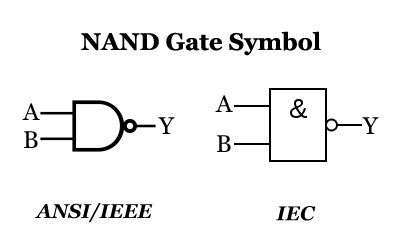
Il cancello NAND è un circuito logico di base di un circuito digitale. È una sovrapposizione di cancelli AND e NOT, con più ingressi e una uscita.
Viene eseguita prima l’operazione AND, seguita dall’operazione NOT. Quando entrambi gli ingressi sono alti (1), l’uscita è bassa (0); se almeno uno degli ingressi è basso (0), l’uscita è alta (1).
Il simbolo logico e la tabella di verità del cancello NAND sono i seguenti:
| Input | Output | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Cancello NOR
Il cancello NOR è l’elemento di base nel circuito logico digitale, che realizza la funzione logica OR. Ha più ingressi, 1 uscita e il cancello NOR multi-ingresso può essere composto da un cancello NOR a 2 ingressi e un inverter.
L’uscita è alta (logica 1) quando entrambi gli ingressi A e B sono bassi (logica 0). Quando uno qualsiasi degli ingressi è alto (logica 1), l’uscita è bassa (logica 0).
L’espressione matematica della sua relazione logica è: Y=A+B, il simbolo logico e la tabella di verità del cancello NOR sono mostrati nella tabella sottostante.

| Input | Output | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Cancello XOR
Un gate XOR è un gate logico che implementa un XOR logico nella logica digitale. Ci sono più ingressi e un’uscita, e il gate XOR multi-ingresso può essere composto da gate XOR a due ingressi.
Se i livelli dei due ingressi sono diversi, l’uscita è un livello alto 1; se i livelli dei due ingressi sono uguali, l’uscita è un livello basso 0. In altre parole, se i due ingressi sono diversi, il gate XOR emette un livello alto 1.
L’espressione logica del gate XOR: Y=A⊕B=A⋅B’+A’⋅B, il simbolo logico e la tavola di verità del gate XOR sono i seguenti:
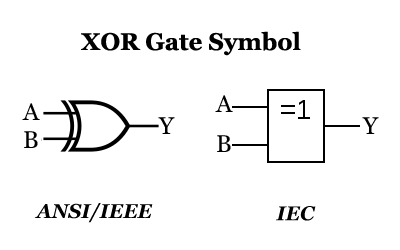
| Input | Output | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Gate XNOR
Il gate XNOR, chiamato anche gate di equivalenza, è l’unità di base del circuito logico digitale. È formato aggiungendo un gate NOT all’uscita del gate XOR e ha 2 terminali di ingresso e 1 terminale di uscita.
Quando uno e solo uno dei due ingressi è basso (logica 0), l’uscita è bassa. Quando i livelli ai 2 ingressi sono uguali, l’uscita è alta (logica 1).
Espressione logica: F=A≡B=A⋅B+A’⋅B’=(AB)’, il simbolo logico e la tavola di verità del gate XNOR sono i seguenti:
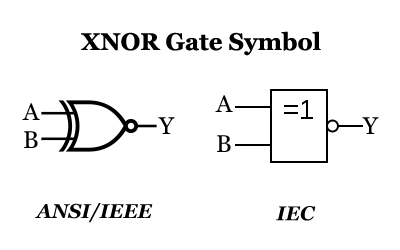
| Input | Output | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |






