Qu'est-ce qu'un circuit RLC ?
Un circuit RLC est un circuit électrique qui contient une résistance (R), une inductance (L) et un condensateur (C) connectés en série ou en parallèle. Ces composants fonctionnent ensemble pour stocker et transférer de l'énergie, ce qui entraîne des oscillations à une fréquence de résonance spécifique. Les circuits RLC sont couramment utilisés dans diverses applications, notamment les filtres, les oscillateurs et les circuits d'accord.
Types de circuits RLC
Les circuits RLC peuvent être principalement divisés en plusieurs types :
Circuit série RLC :
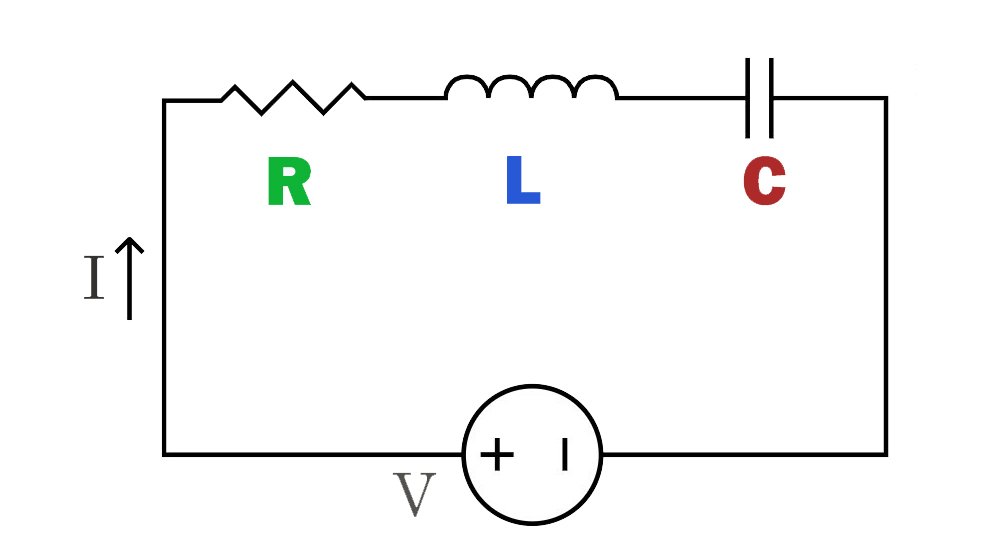
Dans ce circuit, les composants résistance (R), inductance (L) et condensateur (C) sont connectés en série sur le même chemin. Le courant traverse successivement la résistance, l'inductance et le condensateur, ce qui entraîne une variation correspondante du courant dans chaque composant.
Le circuit RLC en série présente des caractéristiques de sélectivité en fréquence, avec des impédances et des réponses différentes selon les fréquences. Il est donc largement utilisé dans les filtres et les circuits accordés.
Circuit parallèle RLC :
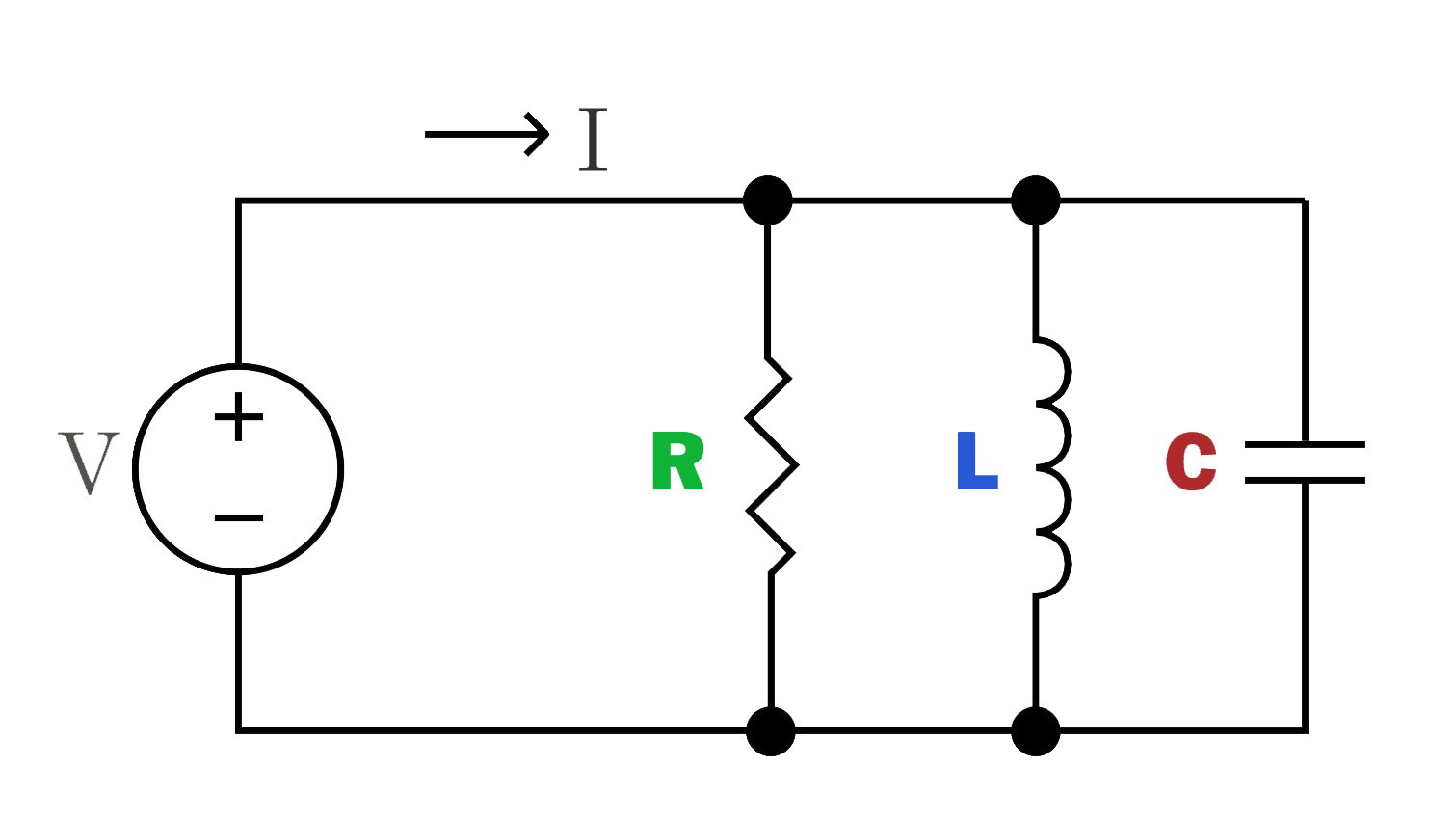
Le circuit RLC parallèle consiste à connecter respectivement la résistance, l'inductance et le condensateur en parallèle. Le courant est divisé entre les branches, et la tension passant à travers chaque composant est la même.
Ce circuit présente des caractéristiques d'impédance pour le courant à une fréquence spécifique, qui peuvent être utilisées pour laisser passer ou bloquer de manière sélective les signaux de certaines fréquences.
Comment mesurer la tension dans un circuit RLC ?
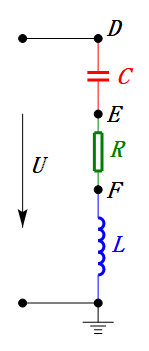
Comme le montrent les schémas ci-dessous :
Lorsque U est une tension sinusoïdale, ce circuit comporte trois points potentiels D, E et F. Ces trois formes d'onde peuvent être observées à l'aide d'un oscilloscope ou mesurées à l'aide d'un voltmètre CA pour UD, UE, UL, UR et UC. Le graphique dynamique à droite reflète les variations de ces cinq tensions au fil du temps dans un scénario donné. Dans le graphique dynamique, UF est équivalent à UL, et idéalement, il devrait y avoir une autre tension UDF, mais j'ai choisi de ne pas inclure les tensions avec des indices à deux lettres pour plus de simplicité.
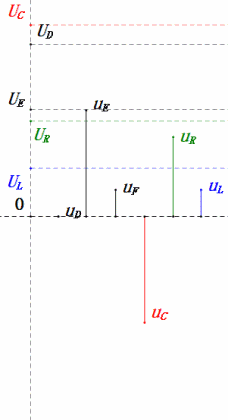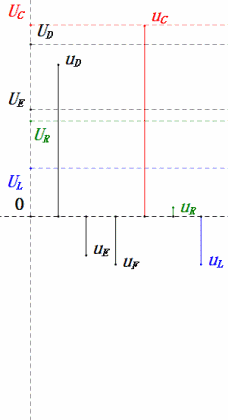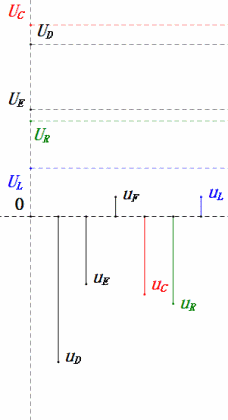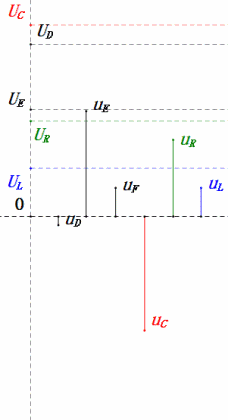
Formule de calcul de la tension
La méthode des phaseurs est une solution brillante qui facilite la résolution des problèmes, mais qui peut nous faire passer à côté des processus dynamiques fascinants illustrés dans le graphique ci-dessus. Avec une réactance inductive XL, une résistance R et une réactance capacitive XC, la méthode des phaseurs pour résoudre ce circuit est décrite comme suit :
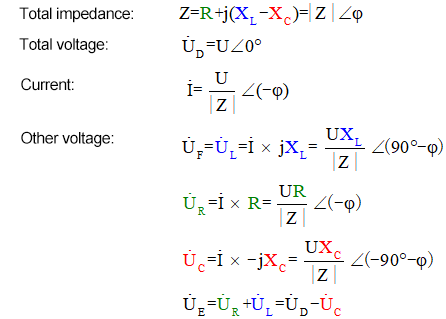
Le voltmètre CA mesure UR ≠ UE – UL. Si L est une inductance idéale, ces trois éléments formeront un triangle rectangle. De même, UC, UD et UE formeront également un triangle, mais pas nécessairement un triangle rectangle. Cela ne signifie pas pour autant que la loi de Kirchhoff sur les tensions (KVL) est violée. Si la valeur instantanée u à un certain moment est mesurée, on constate que uR = uE – uL et uC = uD – uE. De plus, bien que le courant ne soit pas mesuré, les variations de UR sont en phase avec les variations de courant.
Action du signal sinusoïdal et état de résonance
Lorsqu'un signal sinusoïdal est appliqué, la réactance inductive XL = ωL et la réactance capacitive XC = (ωC)^-1. L'état dans lequel ces deux valeurs sont égales est appelé résonance, ce qui nous permet de calculer une fréquence angulaire de résonance ω0.
Dans la section suivante, nous définirons les paramètres pour créer des diagrammes de phaseurs, des diagrammes d'ondes sinusoïdales statiques et des animations des variations instantanées de la tension à 0,5ω0, ω0 et 2ω0.
Tension sous différentes fréquences angulaires résonnantes
Paramètres du modèle :
- U = 6,00 mV
- R = 2,00 Ω (courant effectif inférieur à 3,00 mA, généralement sans danger pour les composants)
- C = 125 μF
- L = 0,500 mH
ω0 calculé = 4000 rad/s (correspondant à une fréquence d'environ 637 Hz, en ignorant les effets du rayonnement électromagnétique pour faciliter la modélisation. Les diagrammes de phaseurs et les diagrammes d'ondes sinusoïdales utilisent des valeurs RMS ; pour les valeurs de crête, multiplier par 1,414)
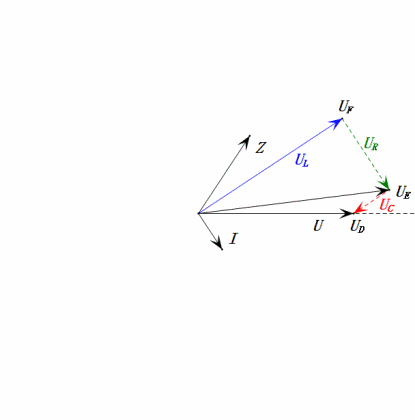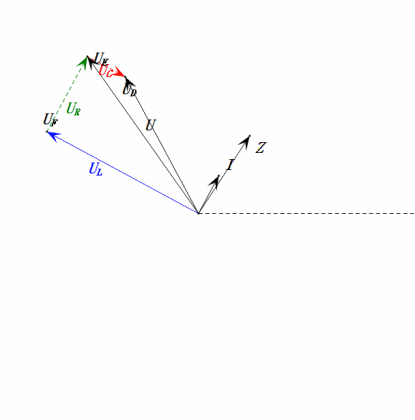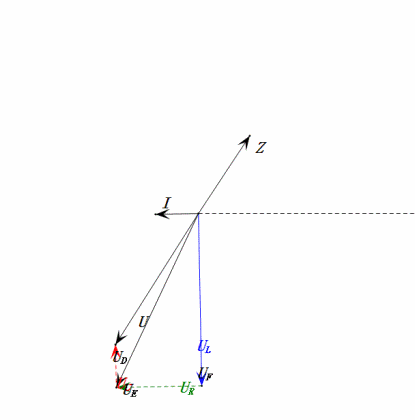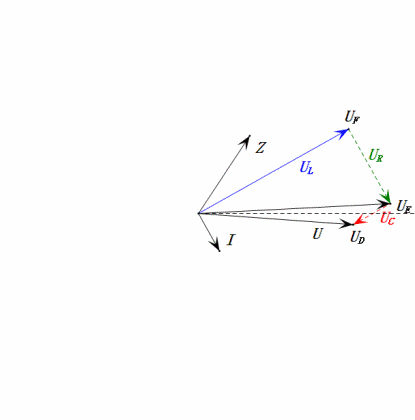
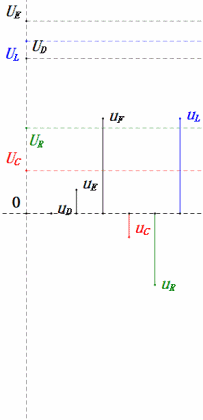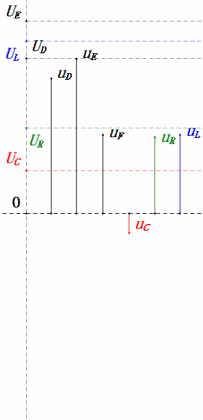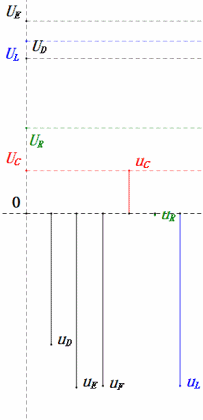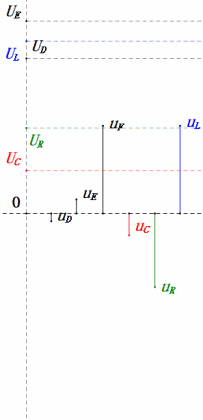
Tension dynamique inférieure à 0,5 ω0
Après avoir effectué les calculs, nous pouvons tracer le diagramme des phaseurs et le diagramme sinusoïdal statique au moment initial :
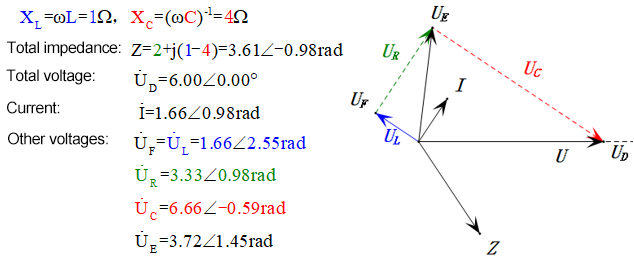
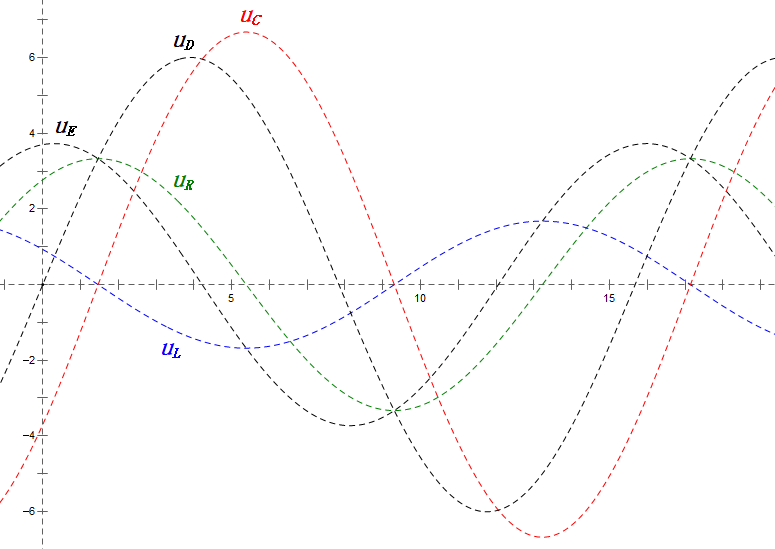
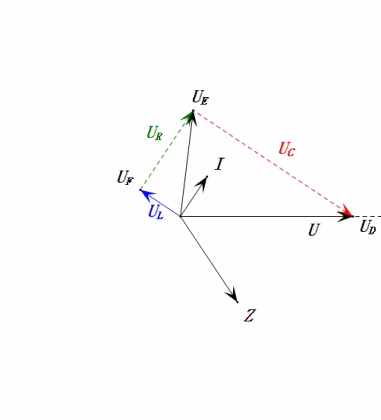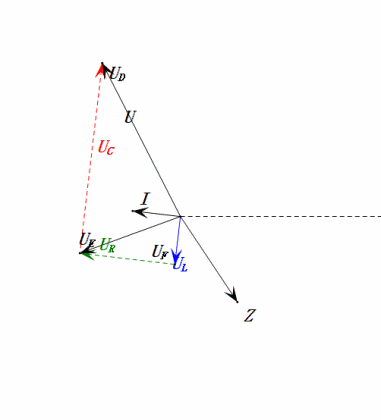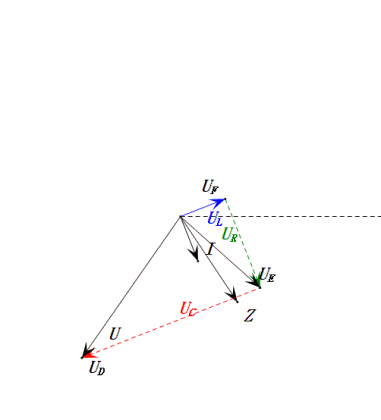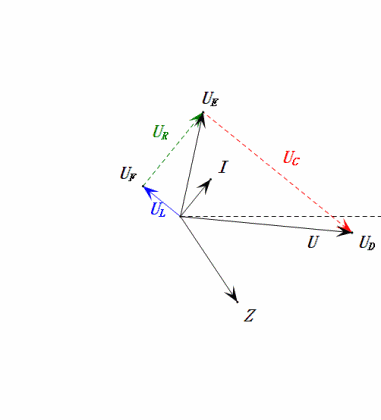
Analyse :
- Courant maximal ≈ 1,57 mA, sans danger pour les composants.
- Le diagramme des phaseurs forme un trapèze droit sans tenir compte de l'UDF.
- À 0,5ω0, XL < XC → UL plus petit, UC plus grand. Le uC maximal dépasse la tension d'alimentation, ce qui peut endommager le condensateur.
- uC est en retard sur uD de ≈30° ; la charge commence pendant la phase ascendante de uD et se termine lorsque uR = 0.
- Le diagramme sinusoïdal montre que uR = uE – uL et uC = uD – uE à chaque instant.
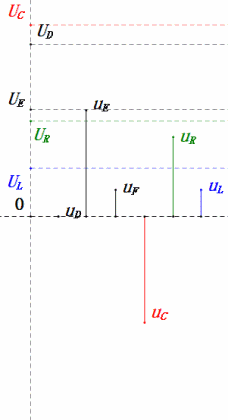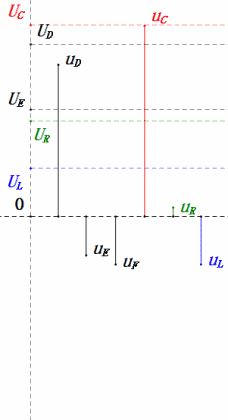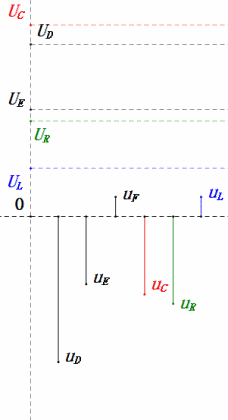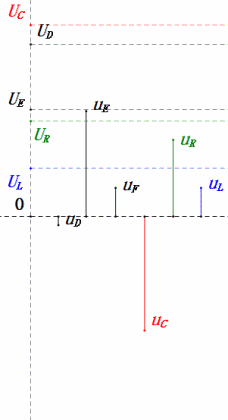
Tension dynamique inférieure à 1ω0
Après avoir effectué les calculs, nous pouvons tracer le diagramme des phaseurs et le diagramme sinusoïdal statique au moment initial :
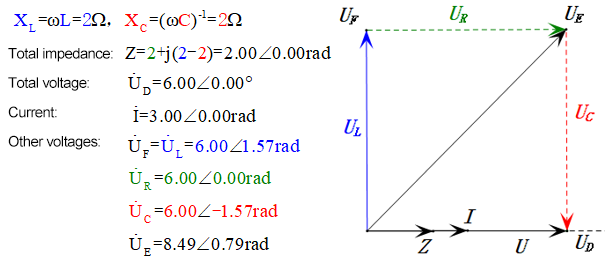
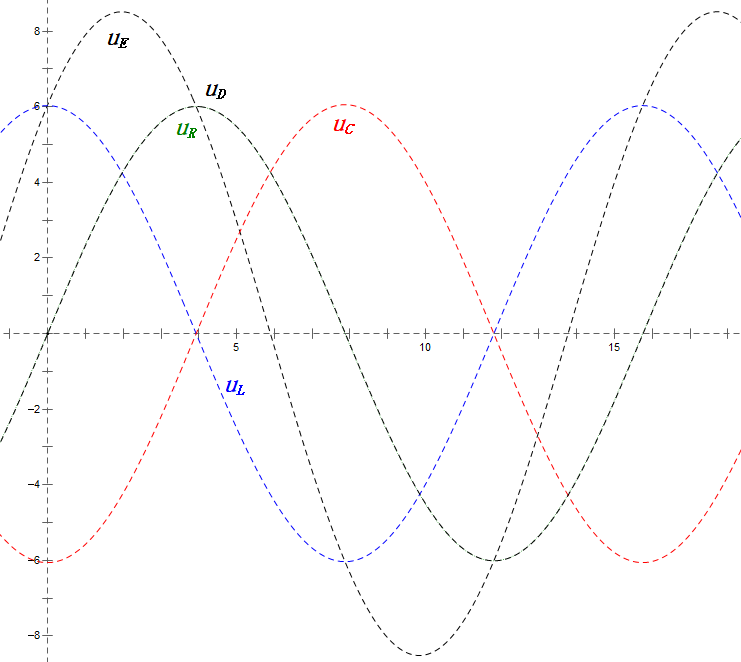
Analyse :
- Courant maximal ≈ 4,24 mA, sans danger pour les composants.
- Le diagramme des phases forme un carré à la résonance (XL = XC).
- Le uE maximal dépasse la tension d'alimentation, mais l'impact sur les composants n'est pas clair.
- Coïncidence : XL = XC = R → uL et uC s'annulent dans le diagramme sinusoïdal, mais les variations de courant affectent les amplitudes.
- Impédance minimisée, courant maximisé à la résonance en raison de l'effet « courant maximal ».
- uC est en retard de 90° exactement par rapport à uD ; la charge commence lorsque uD atteint son pic et se termine lorsque uR = uD = 0.
- Les segments du diagramme sinusoïdal représentent la moitié du temps du cas 1.
- UD = UR, UL = UC maximum en raison des paramètres, mais le fait que les quatre tensions soient égales est une coïncidence.
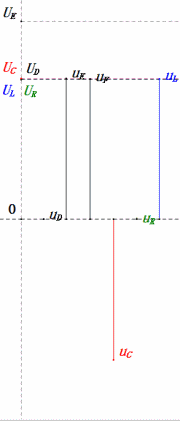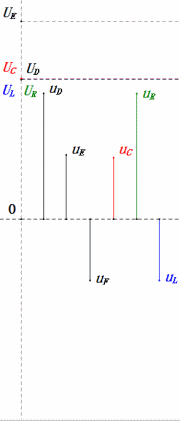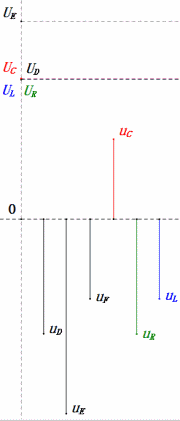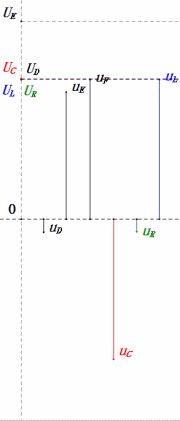
Tension dynamique sous 2ω0
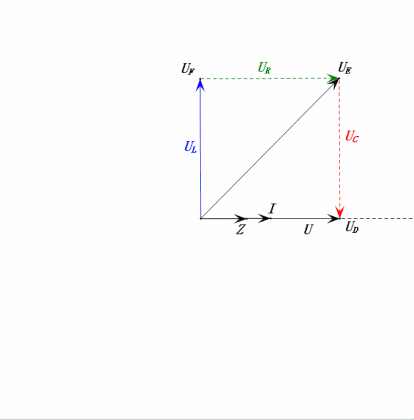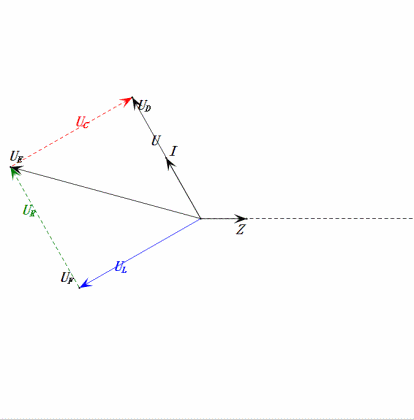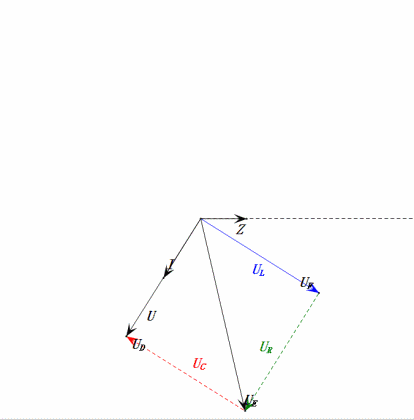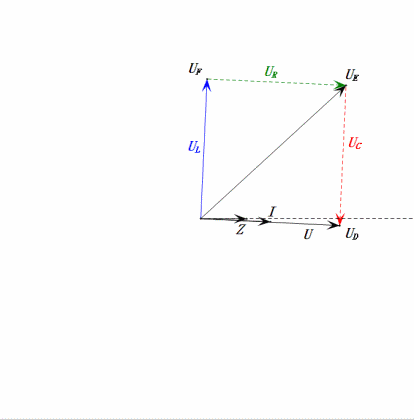
Après avoir effectué les calculs, nous pouvons tracer le diagramme des phaseurs et le diagramme sinusoïdal statique au moment initial :
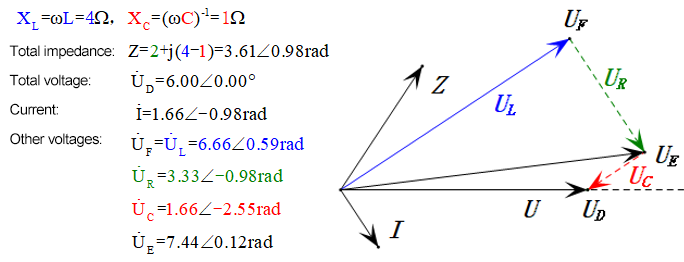
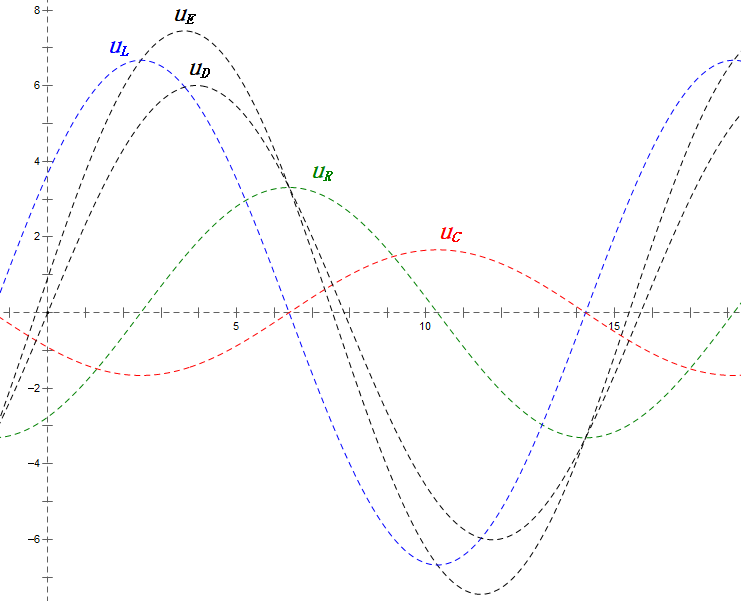
Analyse :
- Courant maximal ≈ 1,57 mA, sans danger pour les composants.
- Le diagramme des phases forme un trapèze droit.
- À 2ω0, XL > XC → UL plus grand, UC plus petit. Les valeurs maximales uL et uE dépassent la tension d'alimentation, ce qui soulève des inquiétudes quant à l'endommagement de l'inductance.
- uC est en retard de ≈150° par rapport à uD ; la charge commence lorsque uD chute à ≈la moitié de sa valeur maximale et se termine lorsque uR = uD = 0.
- Les segments du diagramme sinusoïdal représentent la moitié du temps du cas 2.
- Les équations uR = uE – uL et uC = uD – uE sont valables à tout moment.