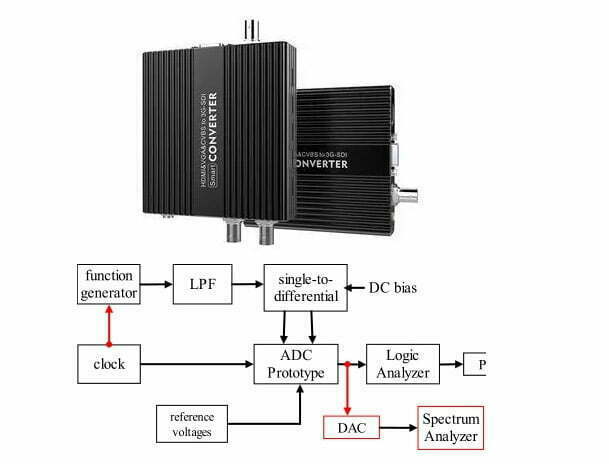
Tra gli strumenti intelligenti, i convertitori ADC e DAC svolgono un ruolo fondamentale. Sappiamo che i microprocessori ampiamente utilizzati attualmente possono gestire solo segnali digitali discreti. Non c’è modo di inserire un segnale analogico continuo dal mondo fisico in un microprocessore senza un ADC. Inoltre, senza un DAC, non c’è modo di emettere un segnale analogico da un microprocessore. (clicca qui per saperne di più sul segnale digitale e sul segnale analogico)
Convertitore analogico-digitale (ADC)
Definizione di ADC
Nel sistema di strumentazione, è spesso necessario convertire le quantità analogiche continuamente variabili rilevate come temperatura, pressione, portata, velocità, intensità luminosa, ecc. in quantità digitali discrete prima di inserirle nel computer per l’elaborazione. Queste quantità analogiche vengono convertite in segnali elettrici (di solito segnali di tensione) da sensori e, dopo essere state amplificate da amplificatori, devono essere sottoposte a determinate elaborazioni per diventare quantità digitali. Un dispositivo che converte l’analogico in digitale è solitamente chiamato convertitore analogico-digitale (ADC), o A/D in breve.
Principio di funzionamento di ADC
In circostanze normali, la conversione A/D generalmente deve passare attraverso quattro processi di campionamento, mantenimento, quantizzazione e codifica.
Campionamento e mantenimento
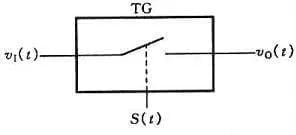
Il campionamento consiste nel convertire una quantità analogica che varia continuamente nel tempo in una quantità analogica discreta nel tempo. Il diagramma schematico del processo di campionamento è mostrato nella Figura 1. La Figura (a) è una struttura del circuito di campionamento, in cui il gate di trasmissione è controllato dal segnale di campionamento S(t), durante la larghezza dell’impulso θ di S(t), il gate di trasmissione è acceso, il segnale di uscita vO(t) è il segnale di ingresso v1 e durante (Ts-θ), il gate di trasmissione è chiuso e il segnale di uscita vO(t)=0. Le forme d’onda del segnale nel circuito sono mostrate nella Figura (b).
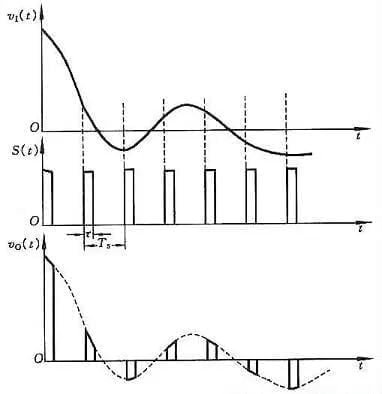
Dall’analisi si può vedere che maggiore è la frequenza del segnale di campionamento S(t), più fedelmente il segnale ottenuto può riprodurre il segnale di ingresso dopo essere passato attraverso il filtro passa-basso. Ma il problema è che la quantità di dati aumenta. Per garantire una frequenza di campionamento appropriata, deve soddisfare il teorema del campionamento.
Teorema del campionamento: supponendo che la frequenza del segnale di campionamento S(t) sia fs e la frequenza della componente di frequenza più alta del segnale analogico di ingresso v1(t) sia fimax, allora fs e fimax devono soddisfare la seguente relazione fs≥2fimax, e fs> è generalmente preso in ingegneria (3~5) fimax.
Ci vuole un certo tempo per convertire il segnale analogico ottenuto dal circuito di campionamento in un segnale digitale ogni volta. Per fornire un valore stabile per il processo di quantizzazione e codifica successivo, il segnale analogico ottenuto ogni volta deve essere mantenuto per un certo periodo di tempo dal circuito di mantenimento.
Il processo di campionamento e mantenimento viene spesso completato contemporaneamente attraverso il circuito di campionamento-mantenimento. Il diagramma schematico e la forma d’onda di uscita del circuito campione-mantenimento sono mostrati nella Figura 2.
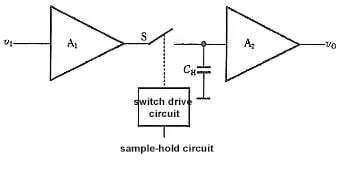
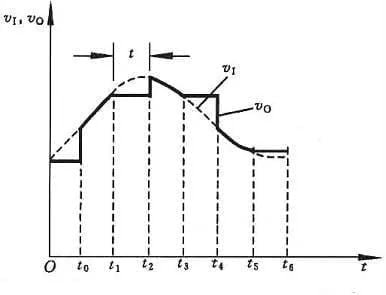
Il circuito è composto da un amplificatore di ingresso A1, un amplificatore di uscita A2, un condensatore di mantenimento CH e un circuito di pilotaggio dell’interruttore. Si richiede che A1 abbia un’elevata impedenza di ingresso nel circuito per ridurre l’influenza sulla sorgente del segnale di ingresso. Per rendere difficile la scarica della carica immagazzinata su CH durante la fase di mantenimento, anche A2 dovrebbe avere un’elevata impedenza di ingresso e A2 dovrebbe anche avere una bassa impedenza di uscita, che può migliorare la capacità di carico del circuito. Generalmente, si richiede anche che AV1⋅AV2=1 nel circuito.
Ora, in combinazione con la Figura 2, analizziamo il principio di funzionamento del campionamento e mantenimento del circuito. A t=t0, l’interruttore S è chiuso e il condensatore si carica rapidamente. Poiché AV1⋅AV2=1, v0=vI, il periodo di campionamento è durante l’intervallo di tempo di t0≤t1. Al tempo t=t1 S viene disconnesso. Se l’impedenza di ingresso di A2 è infinita e S è un interruttore ideale, si può considerare che il condensatore CH non ha un circuito di scarica e la tensione ai suoi capi rimane costante a v0. La sezione piatta da t1 a t2 nella Figura 11.8.2(b) è la fase di mantenimento.
Il circuito di campionamento e mantenimento può essere prodotto da vari tipi di circuiti integrati monolitici. Ad esempio, ci sono AD585 e AD684 per la tecnologia bipolare; AD1154 e SHC76 per la tecnologia mista.
Quantizzazione e codifica
I segnali digitali non sono solo discreti nel tempo, ma anche discontinui in ampiezza. La dimensione di qualsiasi quantità digitale può essere solo un multiplo intero di una specifica unità di quantità minima. Per convertire il segnale analogico in una quantità digitale, nel processo di conversione A/D, la tensione di uscita del circuito di campionamento e mantenimento deve anche essere normalizzata al livello discreto corrispondente in un certo modo approssimativo. Questo processo di conversione è chiamato quantificazione. Il valore quantizzato deve infine essere rappresentato da un codice attraverso il processo di codifica. Il codice ottenuto dopo la codifica è la quantità digitale in uscita dal convertitore A/D.
La più piccola unità di quantità presa nel processo di quantizzazione è chiamata unità di quantizzazione, rappresentata da Δ. È la quantità analogica corrispondente a quando il bit meno significativo del segnale digitale è 1, ovvero 1LSB.
Nel processo di quantizzazione, poiché la tensione di campionamento non è necessariamente divisibile per Δ, c’è inevitabilmente un errore prima e dopo la quantizzazione. Questo errore è chiamato errore di quantizzazione ed è rappresentato da ε. L’errore di quantizzazione è un errore di principio, che non può essere eliminato. Più bit ha il convertitore A/D, più piccole sono le differenze tra i livelli discreti e più piccolo è l’errore di quantizzazione.
Due metodi di quantizzazione approssimativa sono spesso utilizzati nel processo di quantizzazione: solo la quantizzazione di arrotondamento e la quantizzazione di arrotondamento.
solo arrotondamento del metodo di quantizzazione
Prendendo come esempio un convertitore A/D a 3 bit, supponiamo che il segnale di ingresso v1 vari da 0 a 8V. Quando si utilizza il metodo di quantizzazione di arrotondamento, si prende Δ=1V e si scarta la parte che non è sufficiente nell’unità di quantizzazione. Se il valore è compreso tra 0 e 8V La tensione analogica tra 1V è considerata 0Δ, rappresentata dal numero binario 000, e la tensione analogica tra 1V e 2V è considerata 1Δ, rappresentata dal numero binario 001… L’errore massimo di questo metodo di quantizzazione è Δ.
metodo di quantizzazione di arrotondamento
Se si adotta il metodo di quantizzazione di arrotondamento, l’unità di quantizzazione Δ=8V/15 viene utilizzata e la parte inferiore della metà dell’unità di quantizzazione verrà scartata durante il processo di quantizzazione e la parte uguale o superiore alla metà dell’unità di quantizzazione verrà trattata come un’unità di quantizzazione. Tratta la tensione analogica tra 0 ~ 8V/15 come 0Δ, rappresentata da binario 000, e la tensione analogica tra 8V/15 ~ 24V/15 è considerata 1Δ, rappresentata dal numero binario 001 significa attendere.
Confronto
L’errore di quantizzazione massimo ϵmax=1LSB nel precedente metodo di quantizzazione con solo arrotondamento e il metodo di quantizzazione ϵmax=1LSB/2 nel successivo metodo di quantizzazione con arrotondamento e arrotondamento, l’errore di quantizzazione di quest’ultimo è inferiore al primo, quindi è un convertitore A/D maggioritario utilizzato.
Con il rapido sviluppo dei circuiti integrati, nuove idee di progettazione e tecniche di fabbricazione per i convertitori A/D emergono in un flusso continuo. Vengono progettati convertitori A/D con strutture e prestazioni diverse per soddisfare varie esigenze di rilevamento e controllo.
Tipi di ADC
ADC integratore
principio di conversione
Il principio di conversione dell’ADC integratore si basa sull’integrazione della tensione e sul confronto della tensione integrata con un’altra tensione per controllare il conteggio e l’output del conteggio è l’output dell’ADC. L’oggetto dell’integrazione si basa sia sulla tensione di riferimento, sia sulla tensione di riferimento e sulla tensione di ingresso.
Pro e Contro
Vantaggi:
- L’ADC integratore ha un’alta risoluzione e il numero di cifre può essere 12 o addirittura superiore.
- La linearità è molto buona. Essenzialmente, l’ingresso viene confrontato con una tensione di riferimento integrata per determinare l’output, quindi la linearità dipenderà dall’accuratezza del comparatore.
- La topologia di realizzazione del circuito è semplice e ci sono relativamente pochi componenti utilizzati per realizzare questi dispositivi, quindi il circuito è relativamente semplice e il costo di produzione è basso.
Svantaggio:
- Lo svantaggio principale è la lenta velocità di conversione. ADC a N bit, l’output potrebbe richiedere fino a 2 N cicli di clock per convertire un singolo punto campione.
Applicazioni
Utilizzato principalmente in applicazioni di sensori e dispositivi come voltmetri e amperometri dove l’accuratezza è più importante della velocità. In altre parole, la velocità di campionamento dell’ADC integratore è relativamente bassa, ma l’accuratezza è molto alta.
classificazione
Esistono diversi tipi di ADC integratori e i comuni sono integrali a pendenza singola e doppia. Aggiungere una “pendenza” aumenta la precisione a scapito del tempo di conversione.
ADC integratore a pendenza singola
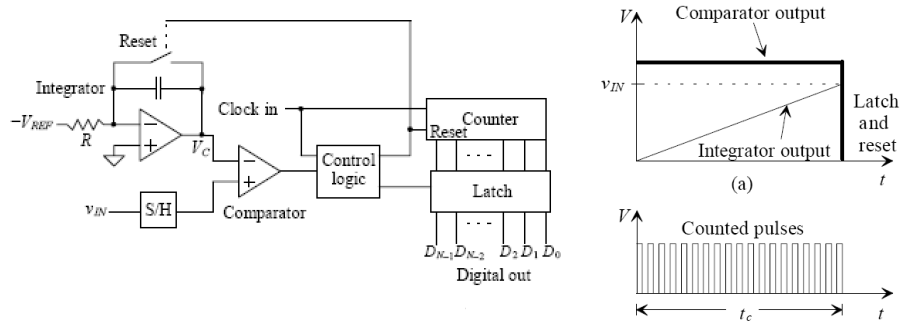
Il comparatore confronta la tensione di ingresso con il valore della tensione di riferimento integrata (nota che la renderemo negativa poiché è collegata all’ingresso invertente dell’amplificatore operazionale). Conta simultaneamente il numero di cicli di clock. Quando l’output dell’integratore è uguale, il comparatore emette una logica “0”, attivando un reset del contatore e dell’integratore e il latch mantiene l’output digitale.
VINVREFVrefVrefVin
Questo è il tempo di conversione. So perché questo ADC integratore è lento. Diamo un’occhiata al caso peggiore, supponendo la tensione di ingresso, supponendo, supponendo che sia un ADC a 20 bit, allora!
VIN=VREFTCLK=1ustc=220us=1048576us
ADC integratore a pendenza singola
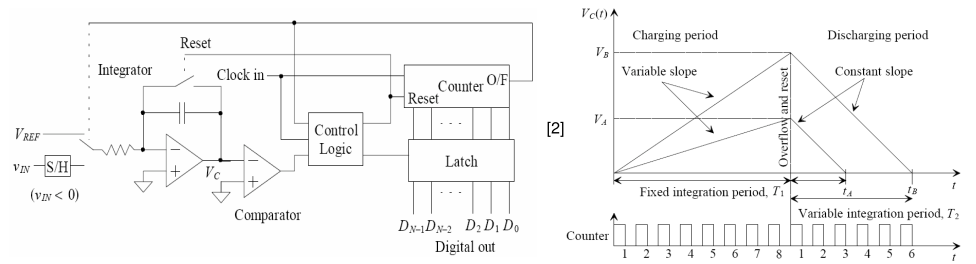
Un ADC a doppia pendenza differisce da un ADC a singola pendenza nel senso che il confronto con la massa viene ora effettuato e vengono integrati due sommatori di tensioni. Inizialmente, l’ingresso negativo è collegato all’integratore, che aumenta fino a quando il contatore non trabocca. Poiché l’integrazione all’ingresso invertente passa a un valore negativo, l’uscita dell’integratore sarà sempre positiva e maggiore di zero, quindi il contatore continuerà a funzionare fino a quando non trabocca, il che richiede 2N cicli di clock (=T1).
VCVREFVINVC
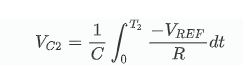
Al tempo T2, sarà uguale alla somma di e, e
VC=VC1+VC2=0
Ma:
VIN/VREF=T2/T1
Pertanto, il principio di conversione ADC, l’ADC a doppia pendenza è più lento dell’ADC a singola pendenza, poiché l’integrazione viene eseguita due volte, l’errore relativo alla pendenza dell’integratore verrà annullato, migliorando così l’accuratezza in linea di principio.
Sigma-Delta Σ-Δ ADC
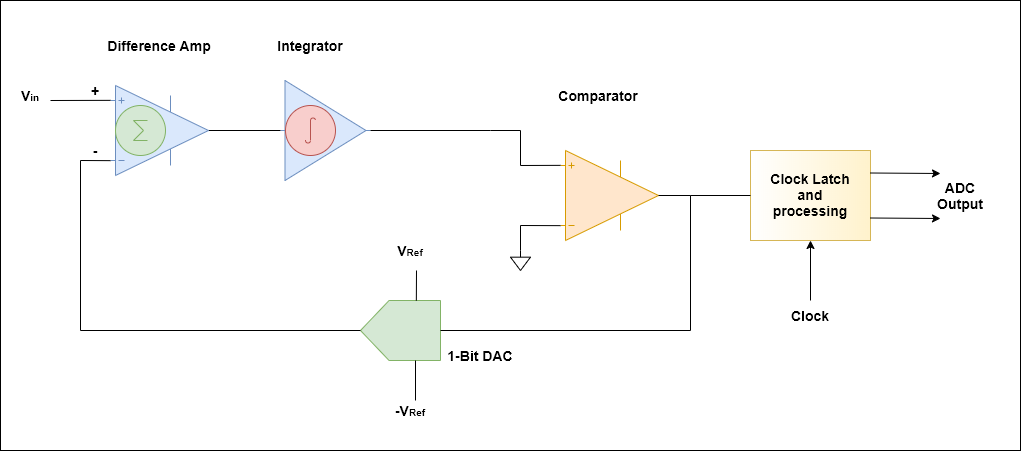
Partendo dall’ingresso, l’amplificatore differenziale produce un’uscita che è la differenza tra Vin e l’uscita del DAC a 1 bit. L’uscita di un DAC a 1 bit può essere uno di due valori: OR . In questa topologia, un integratore può essere considerato come una media mobile del valore precedente e del valore di ingresso corrente.
–Vref+Vref
Pertanto, supponendo che il segmento positivo del comparatore sia inizialmente fissato a un piccolo valore superiore a 0V, il comparatore si inverte. Il suo valore sarà alto o 1. Quindi, l’uscita del DAC sarà . Sull’iterazione successiva, questo valore verrà sottratto dal valore corrente di . Poiché il valore precedente era 0V, l’uscita dell’integratore sarà ora – Vref. A questo punto, l’uscita del comparatore sarà 0 e l’uscita del DAC sarà.
+VrefVin-Vref
Sul campione successivo , l’uscita dell’integratore sarà 0 a causa del valore precedente e l’amplificatore differenziale sottrarrà effettivamente , aggiungendosi così a . L’uscita del comparatore sarà 1.
-Vref-Vref+VrefVin
Questo processo continua iterativamente, quindi, per un ingresso di 0V, l’uscita del comparatore sarà un flusso costante di 101010…. Ricorda che la logica 1 significa , la logica 0 significa , quindi se N campioni vengono campionati e mediati, è facile vedere che il valore medio è 0V. Il blocco di elaborazione dopo il comparatore semplicemente lo emetterà come un singolo valore 0000…, supponendo un valore di riferimento di ( ~ ) o 2 x.
+Vref-Vref-Vref+VrefVref
Ora, supponendo 1V, questo è un ADC da 5V. è ±2.5V. Seguendo gli stessi passaggi di prima iterativamente, l’uscita sarà: 1011101… L’uscita è 1.07V.
Vin±Vref
In sintesi:
Un ADC sigma-delta sovra-campiona il segnale in fase di elaborazione (vedere Come il campionamento analogico-digitale per questo concetto) e filtra passa-basso il segnale da elaborare. Di solito, il numero di bit convertiti utilizzando l’ADC Flash dopo il filtro è inferiore al numero di bit richiesto. Il segnale risultante, insieme agli errori dei livelli discreti FLASH, viene reintrodotto e sottratto dall’ingresso e inviato al filtro. Questo feedback negativo smorza il rumore in modo che non appaia alla frequenza del segnale desiderata. Un filtro digitale dopo l’ADC (utilizzando un filtro di decimazione) riduce la frequenza di campionamento, filtra i segnali di rumore indesiderati e aumenta la risoluzione dell’uscita (da cui il nome modulazione sigma-delta, nota anche come modulazione delta-sigma).
ADC Flash (tipo di confronto diretto)
Il principio dell’ADC FLASH potrebbe essere il più facile da capire. La figura seguente è uno schema di un ADC a 2 bit, che consiste in molti comparatori, ciascuno dei quali è dotato di una tensione di riferimento che è un bit più alta del valore di riferimento precedente. Pertanto, per un ADC a 8 bit, sono necessari 256 di tali comparatori. Per 10 bit, ne servono 1024.
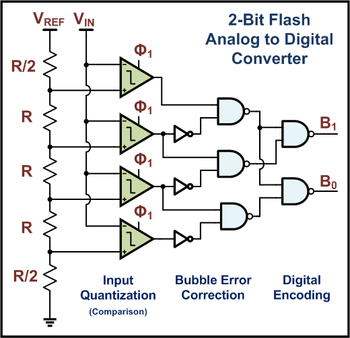
L’ADC FLASH (tipo di confronto diretto) è veloce. Converte direttamente l’ingresso senza alcun campionamento o post-elaborazione pesante. Il problema è che richiede molti comparatori e molti comparatori occupano molto spazio in silicio sul chip. Pertanto, utilizzare gli ADC Flash solo quando è necessario un’elevata velocità che non può essere raggiunta con altre implementazioni di ADC.
Dicotomia incarnata nell'hardware
Nelle applicazioni pratiche, esiste un’altra variante più comunemente utilizzata, l’ADC semi-FLASH. Utilizza un processo in due fasi per ridurre il numero di convertitori necessari nella catena di conversione effettiva:
Innanzitutto, il segnale di ingresso viene confrontato con l’insieme di livelli che si trovano esattamente a metà. Se è inferiore, il bit più significativo, MSB, è impostato su 0 e l’ingresso viene inviato a una catena di comparatori con la tensione di riferimento impostata per convertire il resto dei bit.
Se il segnale di ingresso è superiore, imposta l’MSB su 1, sottrai dall’ingresso. La catena di comparatori viene utilizzata di nuovo per ottenere i bit rimanenti. Quindi, in sostanza, l’ADC FLASH a metà passo sacrifica un confronto extra per risparmiare metà del comparatore. Questo tipo di pensiero può anche continuare a essere dedotto ed espanso, come l’ADC FLASH a 4 punti e così via
Il registro di approssimazione successiva (SAR)
Il registro di approssimazione successiva (SAR) è una parte integrante dell’ADC ad approssimazione successiva. Funziona utilizzando un comparatore per restringere gradualmente l’area contenente la tensione di ingresso. A tal fine, il convertitore confronta la tensione di ingresso con l’uscita di un convertitore digitale-analogico, che in genere indica il punto medio dell’intervallo di tensione scelto. Ad ogni passo del processo, la stima viene memorizzata nel SAR.
Ad esempio, supponiamo che la tensione di ingresso sia di 6,3 V e l’intervallo iniziale sia da 0 a 16 V.
- Per il primo passo, inserisci 6,3 V per confrontare con 8 V (il punto medio dell’intervallo da 0 a 16 V). Il comparatore segnala una tensione di ingresso inferiore a 8 V, quindi il SAR viene aggiornato per ridurre l’intervallo a 0 – 8 V.
- Nel secondo passo, la tensione di ingresso viene confrontata con 4 V (il punto medio da 0 a 8 V), il comparatore segnala che la tensione di ingresso è superiore a 4 V, quindi il SAR viene aggiornato per riflettere che la tensione di ingresso è nell’intervallo da 4 a 8 V.
- Nel terzo passo, la tensione di ingresso viene confrontata con 6 V (metà di 4 V a 8 V); il comparatore segnala una tensione di ingresso superiore a 6 volt e l’intervallo di ricerca diventa da 6 a 8 volt.
Continua questi passaggi fino a raggiungere la soluzione desiderata. La sua topologia è la seguente:
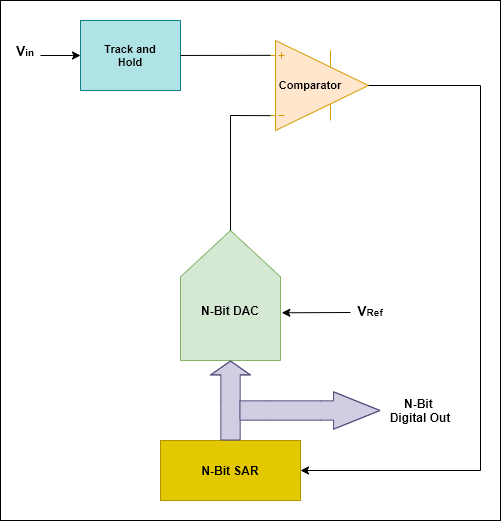
Per l’intuizione, dai un’occhiata alla seguente animazione:
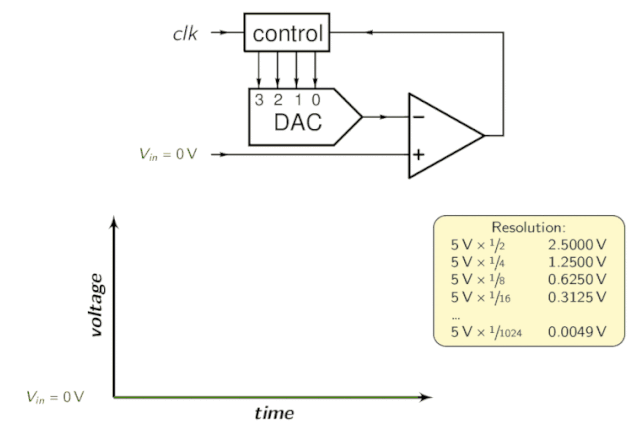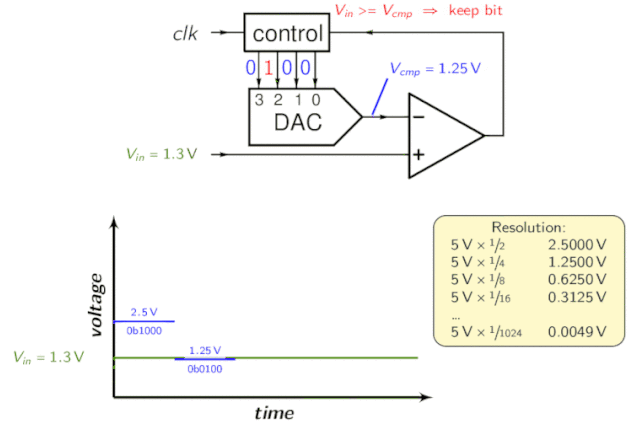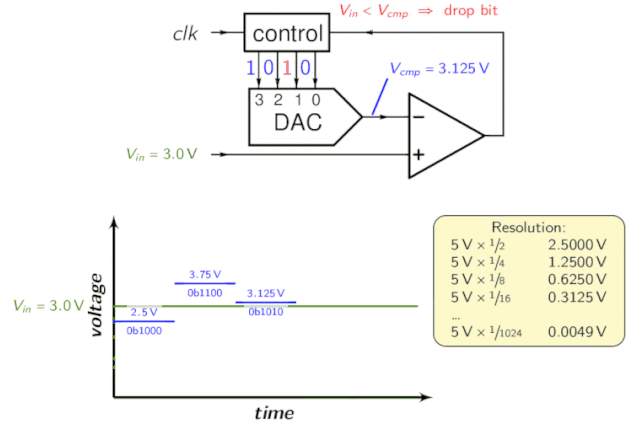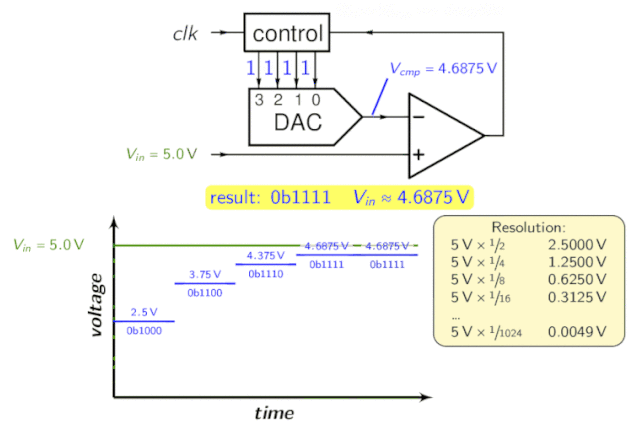
ADC a pipeline
Un ADC a pipeline (noto anche come quantizzatore a subroutine) utilizza due o più pipeline. Innanzitutto, esegui una conversione approssimativa. Nel secondo passaggio, un convertitore digitale-analogico (DAC) viene utilizzato per determinare la differenza nel segnale di ingresso. Questa differenza viene quindi convertita in valori più fini e i risultati vengono combinati in una fase finale. Questo può essere considerato un miglioramento rispetto agli ADC ad approssimazione successiva, dove il segnale di riferimento di feedback consiste in transizioni intermedie sull’intero intervallo di bit (ad esempio, 4 bit), piuttosto che solo il bit più significativo successivo. Combinando i vantaggi del metodo ad approssimazione successiva e dell’ADC flash, questo tipo ha i vantaggi di alta velocità, alta risoluzione e dimensioni dello stampo ridotte.
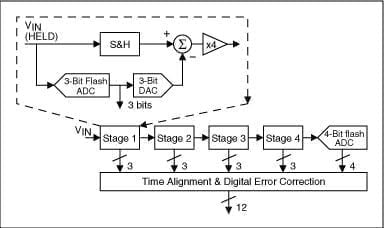
In questo schema, l’ingresso analogico VIN viene prima campionato e mantenuto stabile da un circuito campiona e mantieni (S&H), mentre l’ADC flash nella prima fase lo quantizza a tre bit. L’output a 3 bit viene quindi inviato a un DAC a 3 bit (accurato a 12 bit) e l’output analogico viene sottratto dall’ingresso. Questo “resto” viene ingrandito di un fattore 4 e inviato alla fase successiva (fase 2). Questo resto aggiunto continua attraverso le fasi inferiori della pipeline, fornendo 3 bit per fase, fino a raggiungere l’ADC flash a 4 bit, che risolverà i 4 bit LSB finali. Poiché i bit per ogni fase vengono determinati in momenti diversi, tutti i bit corrispondenti allo stesso campione vengono allineati nel tempo con il registro a scorrimento prima di essere inviati alla logica di correzione degli errori digitali. Nota che quando una pipeline ha finito di elaborare i campioni di ingresso, determinando il bit di acquisizione per questa pipeline e passando il residuo alla pipeline successiva, può iniziare a elaborare il campione successivo ricevuto dal campionatore-mantieni integrato in ciascuna pipeline. Questo pipelining è la ragione dell’elevata produttività, che è anche il concetto di pipelining.
Altri
Oltre ai suddetti ADC comuni, ci sono anche ADC a principio di equilibrio di carica, ADC a condivisione del tempo, ADC FM, ADC di espansione del tempo, ADC a codifica incrementale, ADC Wilkinson, ecc.
Convertitore digitale-analogico (DAC)
Definizione di DAC
La quantità digitale elaborata dal sistema digitale a volte deve essere convertita in una quantità analogica per uso pratico. Questa conversione è chiamata “conversione digitale-analogica”. Il circuito che completa la conversione digitale-analogica è chiamato convertitore digitale-analogico, o DAC (Digital to Analog Converter) in breve.
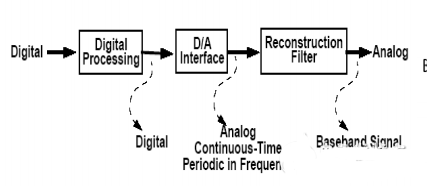
Parametri DAC
Risoluzione
La risoluzione in un DAC è definita come il numero di tutti i possibili livelli di uscita analogici in base a diversi valori di codice digitale di ingresso. Una risoluzione di N bit significa che il DAC può generare 2 N −1 diversi livelli analogici. Generalmente, si riferisce al numero di cifre del codice digitale di ingresso.
Errori di offset e guadagno
L’offset è definito come il valore del segnale analogico di uscita effettivo quando viene inserito un valore di codice pari a 0, e l’errore di guadagno è definito come la differenza tra il valore di uscita a piena scala ideale e il valore di uscita effettivo dopo aver dedotto l’offset, come mostrato nella figura.
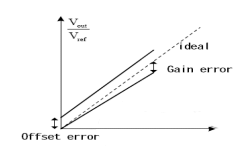
Precisione
La precisione in un DAC è suddivisa in precisione assoluta e precisione relativa. La precisione assoluta è definita come la differenza tra l’uscita ideale e l’uscita effettiva, inclusi vari errori di offset e non linearità. La precisione relativa è definita come l’errore non lineare integrale massimo. La precisione è espressa come rapporto a piena scala, espresso in cifre efficaci. Ad esempio, una precisione di 8 bit significa che l’errore del DAC è inferiore a 1/8 2 dell’uscita a piena scala del DAC. Nota che il concetto di precisione non è correlato alla risoluzione. Un DAC con una risoluzione di 12 bit potrebbe avere solo una precisione di 10 bit; e un DAC con una risoluzione di 10 bit potrebbe avere una precisione di 12 bit. La precisione rispetto alla risoluzione significa che la risposta di trasmissione del DAC può essere controllata in modo più preciso.
Non linearità integrale (INL)
Quando gli errori di offset e di guadagno vengono rimossi, l’errore di linearità integrale è definito come la deviazione della caratteristica di trasferimento effettiva dalla caratteristica di trasferimento ideale (una linea retta). come mostra l’immagine.
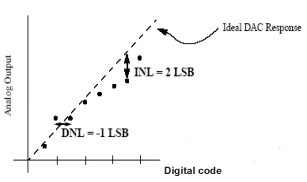
DNL-Non linearità differenziale
In un DAC ideale con un minimo di 1 LSB per variazione di uscita analogica, l’errore di linearità differenziale è definito come la deviazione da 1 LSB per variazione minima dell’uscita analogica (escludendo l’errore di guadagno e l’offset). Il DNL che definiamo è per ogni valore di codice di ingresso digitale e a volte il DNL più grande viene utilizzato per definire il DNL dell’intero DAC. Un DAC ideale avrebbe un errore di linearità differenziale pari a zero per ogni ingresso digitale, mentre un DAC con un DNL massimo di 0,5 LSB avrebbe una variazione di uscita minima compresa tra 0,5 LSB e 1,5 LSB per uscita. Gli errori di linearità integrale e differenziale del DAC sono mostrati nella figura.
Energia del jitter (Area dell'impulso di glitch)
L’area massima sotto il jitter che appare all’uscita dopo la modifica del segnale di ingresso.
Tempo di assestamento
Il tempo di assestamento è entro un intervallo di errore specifico del valore finale e il tempo necessario affinché l’uscita subisca una conversione a scala completa.
Monotonicità Un DAC monotono è un DAC in cui il livello analogico di uscita aumenta sempre all’aumentare del valore del codice digitale di ingresso. Se il DNL massimo è controllato entro 0,5 LSB, allora la monotonicità del DAC può essere garantita naturalmente.
Gamma dinamica spurie (SFDR) SFDR è Gamma dinamica senza spurie, ovvero la gamma dinamica senza rumore e armoniche. Sia il rumore che le armoniche sono chiamati segnali spurii.
Principio del DAC
Converti ogni codice binario di ingresso nella corrispondente quantità analogica in base al suo peso, quindi aggiungi le quantità analogiche che rappresentano ogni bit, la quantità analogica totale ottenuta è proporzionale alla quantità digitale, realizzando così la conversione da quantità digitale a quantità analogica.
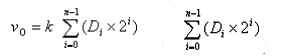
È il valore decimale convertito in un numero binario mediante l’espansione del peso del bit.
Composizione e caratteristiche del DAC
Il DAC è composto principalmente da registri digitali, interruttori elettronici analogici, rete di pesi di bit, amplificatore operazionale di somma e sorgente di tensione di riferimento (o sorgente di corrente costante). Utilizza le cifre delle quantità digitali memorizzate nel registro digitale per controllare gli interruttori elettronici analogici delle cifre corrispondenti rispettivamente, in modo che la cifra con una cifra di 1 generi un valore di corrente proporzionale al suo peso di cifra sulla rete di pesi di cifra, quindi l’amplificatore operazionale controlla ogni valore di corrente sommato e convertito in un valore di tensione.
Le reti di pesi di bit variabili consentono l’assemblaggio di più tipi di DAC, tra cui il DAC a rete di resistenza ponderata, il DAC a rete di resistenza a T invertita R-2R e il DAC a rete di corrente a valore singolo, ecc. La precisione della conversione prodotta dal DAC a rete di resistenza ponderata dipende dall’accuratezza della tensione di riferimento VREF, nonché dalla qualità degli interruttori elettronici analogici, degli amplificatori operazionali e dei valori di resistenza ponderata. Il suo svantaggio è che i valori di resistenza di ogni resistenza di peso sono diversi e quando ci sono molte cifre, i valori di resistenza variano notevolmente, il che porta a grandi difficoltà per garantire la precisione, soprattutto per la produzione di circuiti integrati. Pertanto, nel DAC integrato Questo circuito viene raramente utilizzato da solo.
Indicatori tecnici principali del DAC
Accuratezza e velocità di conversione del DAC: l’accuratezza della conversione è generalmente descritta da risoluzione ed errore di conversione nel DAC.
Risoluzione
In generale, il numero di bit del DAC viene utilizzato per misurare la risoluzione, perché maggiore è il numero di bit, più valori (2n) della tensione di uscita vO e maggiore è la sua capacità di riflettere le sottili variazioni della tensione di uscita. più alta.
Inoltre, la risoluzione può anche essere definita dal rapporto tra la minima tensione di uscita 1 LSB che il DAC può distinguere e la tensione di uscita massima FSR. che è:
risoluzione=1LSB/FSR=k/k(2n-1)=1/(2n-1)
Più piccolo è il valore, maggiore è la risoluzione.
Errore di conversione
L’errore di conversione è la massima deviazione tra la tensione analogica di uscita effettiva e il valore ideale. Comunemente espresso in percentuale o come diversi LSB del rapporto tra questa massima deviazione e FSR. In effetti, è un indicatore completo dei tre errori.
Velocità di conversione
La velocità di conversione è generalmente determinata dal tempo di assestamento. Dal momento in cui l’ingresso cambia da tutti 0 a tutti 1, fino a quando la tensione di uscita si stabilizza entro l’intervallo di FSR±½ LSB (o l’intervallo specificato da FSR±x%FSR), questo periodo è chiamato tempo di assestamento, che è la risposta massima del DAC Tempo, quindi usalo per misurare la velocità di conversione.
Tipi di DAC
Tipo resistivo
La struttura è mostrata nella Figura 1. La Figura 1 mostra un convertitore di tipo ladder R-2R. Il suo vantaggio è che può ottenere una linearità molto buona. Poiché tutte le sorgenti di corrente sono equivalenti, possiamo utilizzare una tecnologia aggiuntiva speciale per rendere più piccolo l’errore tra di esse e la sua struttura è molto più semplice di quella del partitore di resistenza. Lo svantaggio è che la resistenza è sempre non lineare e contiene anche capacità parassita relativa al segnale, quindi è difficile ottenere una corrispondenza completa. Allo stesso tempo, la velocità è limitata dal buffer di uscita e la velocità non può essere molto alta.
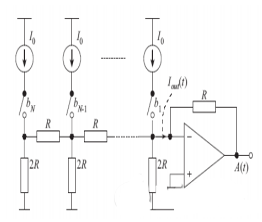
Tipo capacitivo
La struttura è mostrata nella Figura 2. La capacità di ordine superiore CN è 1 2N volte quella della capacità di ordine inferiore C1. Il vantaggio è che il consumo di energia è piccolo e la precisione di corrispondenza è superiore a quella del resistore. I principali fattori limitanti sono la mancata corrispondenza dei condensatori, la resistenza di accensione degli interruttori, i grandi ritardi RC e l’impatto della larghezza di banda limitata dell’amplificatore sulla velocità del DAC. Un importante svantaggio dei DAC a distribuzione di carica è che i condensatori nei processi CMOS occupano una grande area del chip per l’implementazione. Infine, poiché la capacità nel processo CMOS è intrinsecamente non lineare, la linearità dell’intero DAC sarà soppressa. Adatto per alta precisione a banda media e larga.
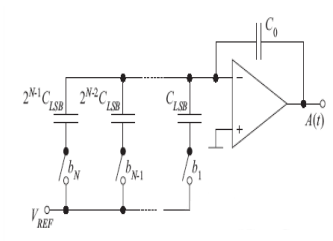
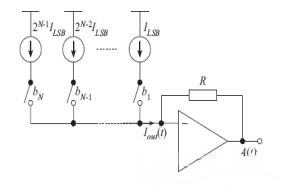
Tipo di corrente
La struttura è mostrata nella Figura 3. Il vantaggio è che quando la precisione è inferiore a 10 bit, l’area può essere resa molto piccola e la velocità non è limitata dalla larghezza di banda dell’amplificatore e dal grande ritardo RC. Può raggiungere un’alta velocità. Poiché tutta la corrente scorre direttamente al terminale di uscita, il consumo di energia è altamente efficiente e facile da implementare. Gli svantaggi sono la sensibilità alla mancata corrispondenza del dispositivo e l’impedenza di uscita limitata della sorgente di corrente. Adatto per requisiti ad alta velocità e banda larga.
È anche possibile non utilizzare un amplificatore operazionale per l’uscita e utilizzare direttamente la resistenza di carico per convertire la corrente in un’uscita di tensione, come mostrato nella Figura 4. Questa forma consente alla velocità del DAC di non essere limitata dalla larghezza di banda dell’amplificatore operazionale.
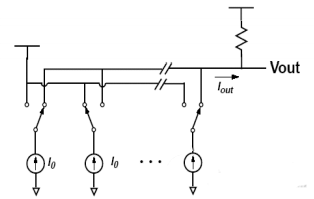
Tipo moltiplicativo
Alcuni dei convertitori DA utilizzano una tensione di riferimento costante, mentre altri aggiungono un segnale CA alla tensione di riferimento in ingresso. Quest’ultimo è chiamato convertitore DA di tipo moltiplicatore perché può ottenere il risultato della moltiplicazione dell’ingresso digitale e dell’ingresso di tensione di riferimento. In generale, un convertitore DA moltiplicatore può non solo eseguire la moltiplicazione, ma anche essere utilizzato come attenuatore per attenuare digitalmente un segnale di ingresso e come modulatore per modulare un segnale di ingresso.
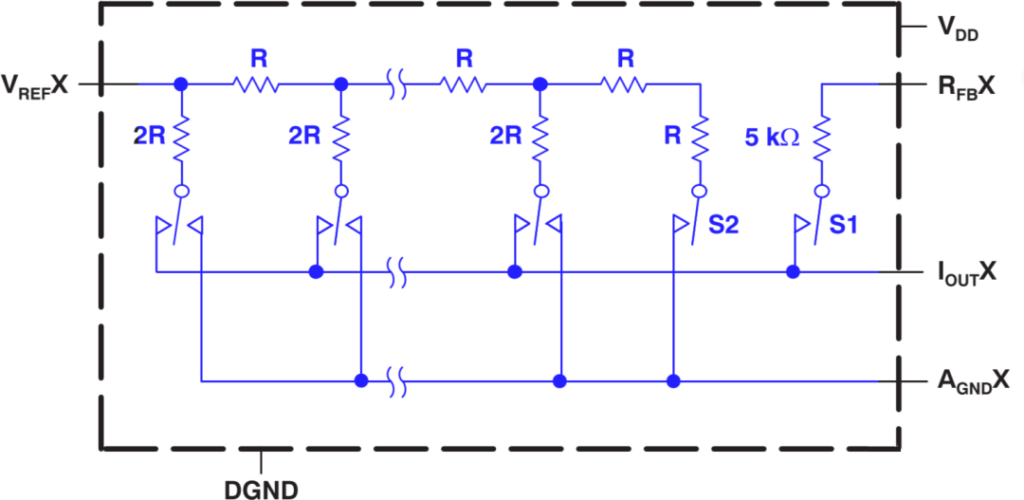
Un convertitore DA
A differenza del sistema di conversione di cui si è appena parlato, un convertitore DA utilizza un metodo speciale per trasformare i valori digitali in una modulazione di larghezza di impulso o modulazione di frequenza, che viene poi livellata con un filtro digitale per produrre una comune uscita di tensione (nota anche come modalità a flusso di bit) per audio, ecc.
Conclusione
Il convertitore ADC e DAC sono due componenti essenziali di qualsiasi sistema digitale. Aiutano a convertire i segnali analogici in segnali digitali e viceversa. L’ADC (Convertitore Analogico-Digitale) accetta un segnale analogico e lo converte in un segnale digitale, mentre il DAC (Convertitore Digitale-Analogico) accetta un segnale digitale e lo converte in un segnale analogico. Entrambi questi componenti sono importanti per un’ampia gamma di applicazioni, dall’elaborazione audio e video alla trasmissione di dati. In questo articolo, abbiamo discusso come funzionano questi convertitori e la loro importanza in diverse applicazioni. Abbiamo anche esplorato i diversi tipi di convertitori, i diversi tipi di segnali che possono convertire e i vantaggi e gli svantaggi di ciascun tipo.