¿Qué es binario?
El binario es un sistema numérico de base 2 inventado por Gottfried Leibniz, uno de los cuatro sistemas numéricos. En este sistema, se representa normalmente mediante dos símbolos diferentes: 0 y 1.

En los circuitos electrónicos digitales, la implementación de puertas lógicas utiliza directamente el sistema binario, que se emplea en los ordenadores modernos y en los dispositivos que dependen de ellos. Cada número se denomina bit (abreviatura de «dígito binario»).
En la lógica booleana, un solo dígito binario solo puede representar verdadero (1) o falso (0); sin embargo, se pueden utilizar varios dígitos binarios para representar números grandes y realizar funciones complejas, cualquier número entero se puede representar en binario.
En la memoria, el almacenamiento, el procesamiento y las comunicaciones de datos digitales, los valores 0 y 1 se denominan a veces «nivel bajo» y «nivel alto», respectivamente.

El término «binario» también se puede utilizar para describir programas de software compilados. Una vez compilado, un programa contiene datos binarios denominados «código máquina» que pueden ser ejecutados por la CPU del ordenador.
¿Qué es Octal?
El sistema octal, abreviado como OCT u O, es un sistema de numeración con base 8. Emplea los ocho dígitos 0, 1, 2, 3, 4, 5, 6, 7, y después del 7 vuelve al 0 e incrementa el dígito superior en 1. En algunos lenguajes de programación, un dígito inicial 0 suele indicar que el número está en octal. Los números octales y los números binarios se corresponden bit a bit (un dígito octal corresponde a tres dígitos binarios), lo que hace que el octal sea útil en los lenguajes informáticos.
El sistema octal se ha utilizado ampliamente en sistemas informáticos como PDP-8, ICL 1900 y grandes ordenadores centrales IBM, que utilizan longitudes de palabra de 12, 24 o 36 bits. Estos sistemas se basan en el sistema octal, ya que sus longitudes de palabra binarias ideales son múltiplos de 3 (cada dígito octal representa tres dígitos binarios). La visualización de cuatro a doce dígitos representa de forma sucinta toda la máquina. También reduce los costes, ya que los dígitos pueden mostrarse a través de pantallas digitales, pantallas de siete segmentos y calculadoras para los paneles de control del operador. Las pantallas binarias son demasiado complejas, las pantallas decimales requieren un hardware complejo y las pantallas hexadecimales exigen mostrar más dígitos.
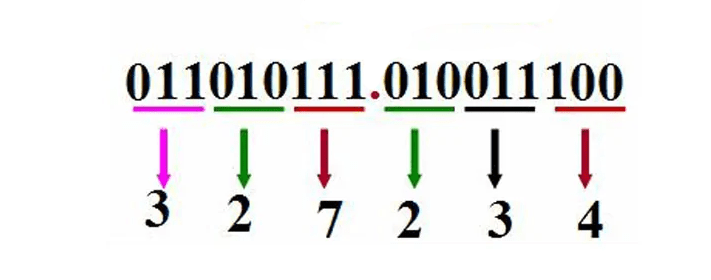
Dado que un dígito hexadecimal corresponde a cuatro dígitos binarios, el sistema hexadecimal es más conveniente para representar el binario. Por lo tanto, la aplicación del sistema octal está menos extendida que la del hexadecimal. Algunos lenguajes de programación ofrecen la posibilidad de representar números utilizando la notación octal, y algunas aplicaciones Unix más antiguas siguen utilizando el sistema octal. Los sistemas informáticos requieren conversiones de sistemas numéricos internamente, utilizando el binario como base. Las conversiones de sistemas numéricos entre binario, octal y decimal se realizan en la programación, y FORTRAN77, centrado en binario y decimal, se encarga de estas conversiones.
Sin embargo, todas las plataformas informáticas modernas utilizan sistemas de 16, 32 o 64 bits, donde las plataformas de 64 bits se dividen a su vez en bytes de 8 bits. En estos sistemas, tres dígitos octales satisfacen cada requisito de byte, y el dígito octal más significativo representa dos dígitos binarios (con +1 para el siguiente byte, si procede). Representar palabras de 16 bits en octal requiere 6 dígitos, pero el dígito octal más significativo representa solo 1 dígito binario (0 o 1). Esta limitación impide que los bytes sean fáciles de leer, ya que dan como resultado dígitos octales de 4 bits.
Como resultado, el sistema hexadecimal se utiliza ahora más comúnmente en los lenguajes de programación, ya que dos dígitos hexadecimales especifican completamente un byte. Las plataformas con potencias de dos y tamaños de palabra hacen que las instrucciones sean más comprensibles. La omnipresente arquitectura x86 es un ejemplo de ello, aunque el sistema octal rara vez se utiliza en esta arquitectura. Sin embargo, el sistema octal puede ser útil para describir ciertas codificaciones binarias, como el byte ModRM, que se divide en 2, 3 y 3 bits.
¿Qué es Decimal?
El sistema decimal, a menudo denominado sistema de base 10, es un método de conteo en el que cada diez unidades dan lugar a una unidad superior. El primer dígito tiene un valor posicional de 10^0, el segundo dígito 10^1 y el dígito N 10^(N-1). El valor de un número en este sistema es la suma de cada dígito (valor × peso posicional).
El método de conteo decimal es el más utilizado en la vida cotidiana. Se caracteriza por un incremento de diez entre unidades adyacentes, lo que constituye la base de la notación decimal. Probablemente, esto se deba al hecho de que los seres humanos suelen tener diez dedos, lo que influye en el desarrollo de la aritmética utilizando el sistema decimal. Aristóteles observó que los seres humanos suelen utilizar el sistema decimal debido a la realidad anatómica de tener diez dedos.
Históricamente, la mayoría de los sistemas numéricos escritos desarrollados de forma independiente empleaban una base decimal, excepto los sistemas numéricos sexagesimal babilónico (base 60) y vigesimal maya (base 20). Sin embargo, estos sistemas decimales no eran necesariamente posicionales.
El término «decimal» proviene de la palabra latina «decem», que significa diez. El método de conteo decimal fue inventado por matemáticos hindúes hace unos 1500 años y posteriormente fue transmitido por los árabes en el siglo XI. Se basa en dos principios: la notación posicional y la representación en base diez. Todos los números se componen de los diez símbolos básicos y, cuando una unidad alcanza el diez, se traslada a la siguiente posición, lo que hace que la posición de un símbolo sea crucial. Los símbolos fundamentales son los dígitos del 0 al 9.
Para representar múltiplos de diez, los dígitos se desplazan una posición a la izquierda con un cero al final, lo que da como resultado 10, 20, 30, y así sucesivamente. Del mismo modo, los múltiplos de cien implican volver a desplazar los dígitos: 100, 200, 300, etc. Para expresar una fracción de diez, los dígitos se desplazan a la derecha y se añaden ceros según sea necesario: 1/10 se convierte en 0,1, 1/100 se convierte en 0,01 y 1/1000 se convierte en 0,001.
¿Qué es hexadecimal?
El sistema hexadecimal (abreviado como hex o subíndice 16) es un sistema de numeración con base 16, en el que cada 16 se suma a 1. Normalmente se representa con los números 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 y las letras A, B, C, D, E, F (a, b, c, d, e, f), entre los que A~F representan 10~15, lo que se denomina números hexadecimales.
Por ejemplo, el número 57 en decimal se escribe como 111001 en binario y 39 en hexadecimal. El sistema hexadecimal actual se utiliza ampliamente en el campo de la informática, ya que no es difícil convertir 4 bits (Bit) en números hexadecimales individuales. 1 byte puede representarse como 2 números hexadecimales consecutivos. Sin embargo, esta notación mixta es confusa y requiere algunos prefijos, sufijos o subíndices para mostrarla.
Decimal a binario
La conversión de un número decimal a un número binario implica conversiones separadas para las partes entera y fraccionaria, que luego se combinan.
Para la parte entera, se utiliza el método de «dividir por 2 e invertir los restos». El procedimiento es el siguiente: Dividir el entero decimal por 2, obteniendo un cociente y un resto. Divida el cociente por 2 de nuevo y continúe este proceso hasta que el cociente sea menor que 1. A continuación, tome los restos obtenidos inicialmente como los bits menos significativos del número binario y los restos obtenidos posteriormente como los bits más significativos, ordenándolos en orden inverso.
| Decimal | Binary |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
Por ejemplo, al convertir el número decimal 1 al sistema binario, el resultado es 1B (donde B significa el sufijo binario). Para el número decimal 2, como llegamos a 2, tenemos que llevar 1, lo que da como resultado el número binario 10B. Del mismo modo, al convertir el número decimal 5 a binario, dado que 2 es 10B, entonces 3 es 10B + 1B = 11B, 4 es 11B + 1B = 100B y 5 es 100B + 1B = 101B. Siguiendo este patrón, cuando el número decimal es 254, su representación binaria es 11111110B.
Podemos deducir una regla general al convertir números binarios a números decimales. Comenzando por el bit menos significativo del número binario y retrocediendo, cada bit representa 2 elevado a la potencia de n, donde n indica la posición del bit desde el final. Aquí, n comienza a contar desde 0. Si un bit binario tiene un valor de 1, contribuye a la suma; si es 0, no contribuye. Por ejemplo, hagamos ingeniería inversa del número decimal a partir del número binario 11111110B, siguiendo el proceso de cálculo:
0*20+1*21+1*22+1*23+1*24+1*25+1*26+1*27=254
¿Por qué los ordenadores utilizan el sistema binario?
En primer lugar, el sistema numérico binario utiliza solo dos dígitos: 0 y 1, por lo que cualquier elemento con dos estados estables diferentes puede utilizarse para representar un determinado bit de un número. De hecho, hay muchos componentes con dos estados estables distintos. Por ejemplo, «encendido» y «apagado» de una lámpara de neón; «encendido» y «apagado» de un interruptor; «alto» y «bajo», «positivo» y «negativo» de un voltaje; «sin agujero»; «señal» y «sin señal» en el circuito; polos sur y norte de materiales magnéticos, etc., y la lista continúa. Utilizar estos estados distintos para representar números es fácil de implementar. No solo eso, sino que, lo que es más importante, los dos estados completamente diferentes no solo son cuantitativamente diferentes, sino también cualitativamente diferentes. De esta manera, se puede mejorar en gran medida la capacidad antiinterferencia de la máquina y se puede mejorar la fiabilidad. Es mucho más difícil encontrar un dispositivo sencillo y fiable que pueda representar más de dos estados.
En segundo lugar, las cuatro reglas aritméticas del sistema de conteo binario son muy simples. Además, las cuatro operaciones aritméticas pueden atribuirse en última instancia a la suma y al desplazamiento, de modo que el circuito de la unidad aritmética en la computadora electrónica también se ha vuelto muy simple. No solo eso, sino que la línea se simplifica y se puede aumentar la velocidad. Esto tampoco es comparable al sistema de conteo decimal.
En tercer lugar, el uso de representaciones binarias en los ordenadores electrónicos permite ahorrar equipo. Se puede demostrar teóricamente que el uso del sistema ternario es el que más equipo ahorra, seguido del sistema binario. Sin embargo, debido a que el sistema binario tiene ventajas que otros sistemas binarios, incluido el sistema ternario, no tienen, la mayoría de los ordenadores electrónicos siguen utilizando el binario. Además, dado que en el sistema binario solo se utilizan dos símbolos, «0» y «1», se puede utilizar el álgebra booleana para analizar y sintetizar los circuitos lógicos de la máquina. Esto proporciona una herramienta útil para diseñar circuitos de ordenadores electrónicos. En cuarto lugar, los símbolos binarios «1» y «0» se corresponden exactamente con «verdadero» y «falso» en las operaciones lógicas, lo que resulta conveniente para que los ordenadores realicen operaciones lógicas.
Decimal Vs. Binary Vs. Hexadecimal
El sistema hexadecimal es similar al binario, con la diferencia clave de que el hexadecimal sigue un sistema de «base dieciséis», en el que cada dieciséis cuentas se agrupan juntas. Otro aspecto importante a tener en cuenta es que los números decimales del 0 al 15 se representan en hexadecimal como 0 a 9, seguidos de A, B, C, D, E, F, donde el 10 en decimal corresponde a A en hexadecimal, el 11 a B, y así sucesivamente hasta el 15, que corresponde a F.
Por lo general, denotamos los números hexadecimales añadiendo el sufijo «H» al final, lo que indica que el número está en formato hexadecimal, como AH, DEH, etc. Las mayúsculas y minúsculas no son significativas en este caso. En el contexto de la programación en lenguaje C, los números hexadecimales deben escribirse como «0xA» o «0xDE», donde el prefijo «0x» significa hexadecimal.
La conversión entre números decimales y hexadecimales no se trata aquí, ya que las reglas son similares a las de la conversión entre decimales y binarios. Es fundamental dominar la conversión entre números decimales, binarios y hexadecimales, ya que estas habilidades se utilizan ampliamente, especialmente en la programación de microcontroladores con C.
Para los números entre 0 y 15, que se utilizan con frecuencia en la programación de microcontroladores, la conversión típica consiste en convertir primero el binario a decimal y luego el decimal a hexadecimal. Si le resulta difícil recordar estas conversiones ahora, puede reforzar su memoria a medida que avanza en sus estudios.
Aquí tienes la tabla de conversión de números binarios, decimales y hexadecimales del 0 al 15:
| Decimal | Binary | Hexadecimal |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |