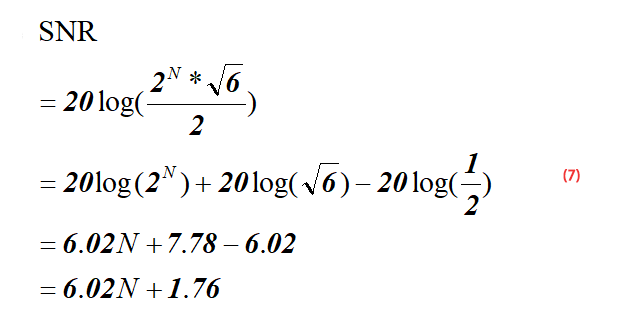Cos'è il rapporto segnale/rumore?
Il rapporto segnale/rumore (SNR) è una misura utilizzata in scienza e ingegneria che confronta il livello di un segnale desiderato con il livello del rumore di fondo. È definito come il rapporto tra la potenza del segnale e la potenza del rumore. Un rapporto superiore a 1:1 indica più segnale che rumore.
Come calcolare il rapporto segnale/rumore?
L’SNR è solitamente espresso in decibel (dB). La formula del rapporto segnale/rumore è:
SNR=10lg(Ps/Pn)
oppure
SNR=20lg(Vs/Vn)
Tra questi, “Ps” e “Pn” rappresentano rispettivamente la potenza efficace del segnale e del rumore, e “Vs” e “Vn” sono i valori efficaci della tensione del segnale e del rumore.
Calcolo di simulazione
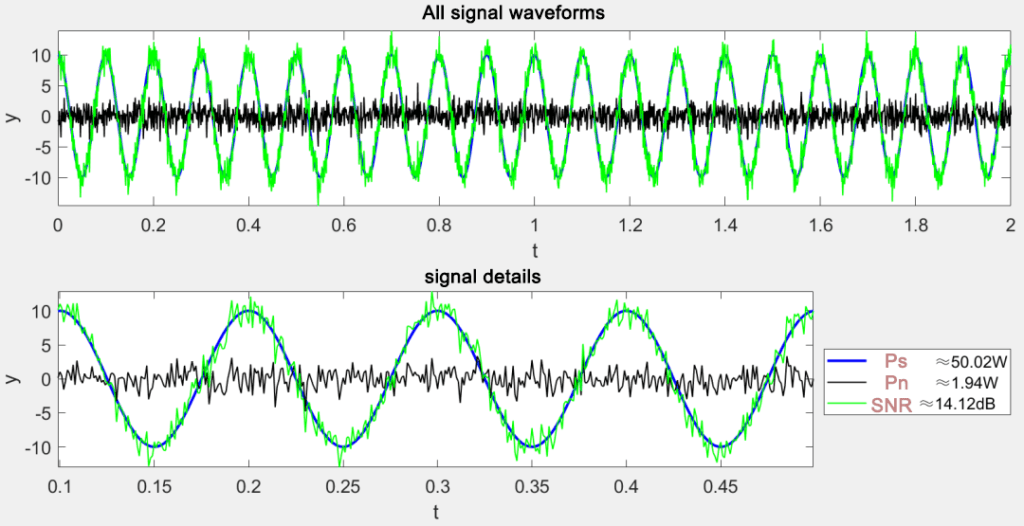
Il caso seguente utilizzerà il rapporto di potenza come esempio per eseguire calcoli di simulazione:
%% Calculating the SNR Simulation
clear; clc; close all; warning off;
% parameter settings
T = 2; % Simulation time
fs = 1000; % Sampling frequency
t = 0 : 1/fs : T;
L = length(t);
A = 10; % Amplitude
fc = 10; % carrier frequency
P_n = 2; % noise power
% generate simulated signal
signal = A * cos(2 * pi * fc .* t); % generate a valid signal
noise = sqrt(P_n) .* randn(1, L); % Generate white Gaussian noise signal
% Calculating SNR
P_s = sum(signal .^ 2) / L; % signal power
P_n = sum(noise .^ 2) / L; % noise power
SNR = 10 * log10(P_s / P_n); % signal-to-noise ratio
fprintf('\t Ps:%.2fW\n', P_s);
fprintf('\t Pn:%.2fW\n', P_n);
fprintf('\t SNR:%.2fdB\n', SNR);
figure(1); clf;
subplot(2, 1, 1);
plot(t, signal, 'b', 'linewidth', 2); hold on;
plot(t, noise, 'k', 'linewidth', 1); hold on;
plot(t, signal+noise, 'g', 'linewidth', 1);
xlabel('t'); ylabel('y'); axis('tight'); title('All waveforms'); set(gca, 'fontsize', 14);
subplot(2, 1, 2);
plot(t(100:500), signal(100:500), 'b', 'linewidth', 2); hold on;
plot(t(100:500), noise(100:500), 'k', 'linewidth', 1); hold on;
plot(t(100:500), signal(100:500)+noise(100:500), 'g', 'linewidth', 1);
legend(['signal power≈', num2str(P_s, '%.2f'), 'W'], ['noise power≈', num2str(P_n, '%.2f'), 'W'], ...
['SNR≈', num2str(SNR, '%.2f'), 'dB'], 'location', 'eastoutside');
xlabel('t'); ylabel('y'); axis('tight'); title('Zoom in to observe signal details'); set(gca, 'fontsize', 14);
set(gcf, 'position', [12, 60, 1450, 650]);
SNR ADC
SNR ADC viene utilizzato per misurare la qualità di un convertitore digitale-analogico (DAC) o di un convertitore analogico-digitale (ADC). Per saperne di più su questi componenti cruciali, consulta la nostra guida su Convertitori ADC e DAC: come funzionano. Più alto è il valore SNR ADC, migliore è la performance del sistema di conversione. È essenziale per qualsiasi sistema di segnale mantenere un buon valore SNR ADC per fornire segnali di output accurati.
Calcolo SNR ADC
formula snr adc:
SNR=6.02N+1.76dB
“N” è il numero di bit dell’ADC.
Derivazione della formula
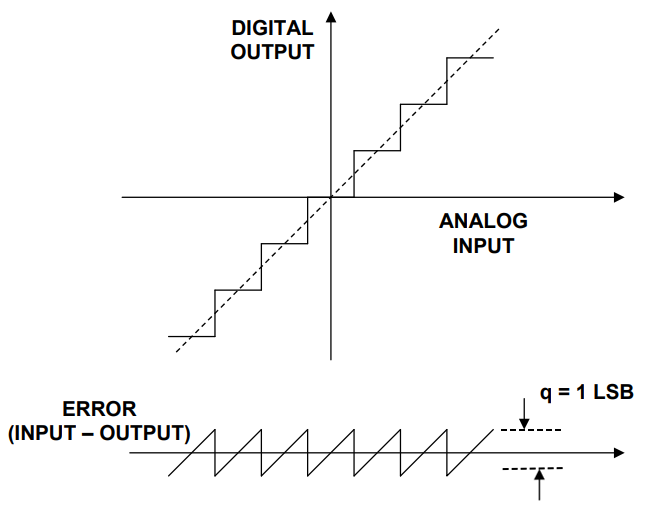
La figura seguente è uno schema del rumore di quantizzazione di un ADC ideale. Come si può vedere dalla figura seguente, per un segnale analogico di ingresso lineare, l’ADC produrrà un output a gradini. La forma d’onda di errore di questo input e output è simile a una sega con valore picco-picco q=1LSB Onda, il suo processo di calcolo del valore RMS effettivo è mostrato nella formula (1) (q=1LSB), il processo di calcolo LSB è mostrato nella formula (2), dove FS è l’intervallo di tensione di ingresso dell’ADC.
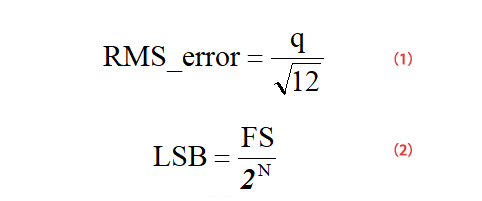
Poiché il rapporto segnale/rumore è il valore efficace (RMS) del segnale diviso per il valore efficace (RMS) del rumore, possiamo ottenere la formula (3):
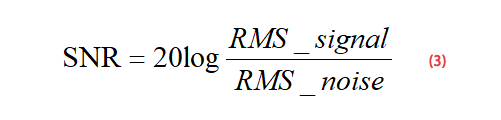
Per un segnale sinusoidale di ingresso a piena scala come mostrato nella formula (4), la formula (5) può essere ottenuta in base alla formula (4):
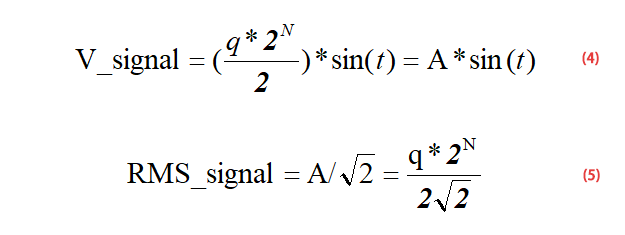
Per un ADC a piena scala, il suo intervallo di ingresso è 0-FS, quindi l’intervallo di ampiezza del segnale sinusoidale di ingresso è 0-Fs/2, vedere lo schema seguente, quindi il denominatore nella formula (4) è 2.
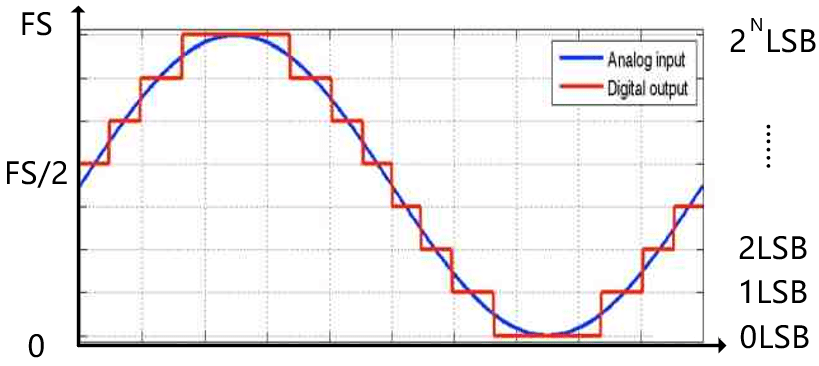
Finora, conosciamo il valore efficace (RMS) del segnale – formula (5) e il valore efficace (RMS) del rumore di quantizzazione ADC – formula (1). Ora inseriamo la formula (5) e la formula (1) nella formula (3) per ottenere la formula (6):
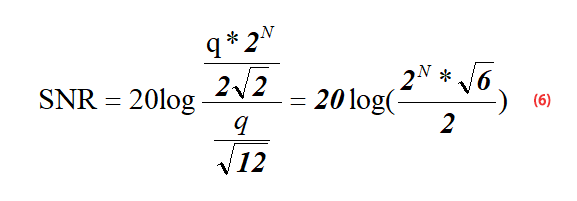
Dopo aver semplificato la formula (6), possiamo ottenere la formula 7 come segue: