Cos'è il binario?
Il binario è un sistema numerico in base 2 inventato da Gottfried Leibniz, uno dei quattro sistemi numerici. In questo sistema, è solitamente rappresentato da due simboli diversi 0 e 1.

Nei circuiti elettronici digitali, l’implementazione di porte logiche utilizza direttamente il binario, che viene utilizzato nei computer moderni e nei dispositivi che si basano su computer. Ogni numero è chiamato bit (abbreviazione di Binary digit).
Nella logica booleana, una singola cifra binaria può rappresentare solo Vero (1) o Falso (0), tuttavia, più cifre binarie possono essere utilizzate per rappresentare numeri grandi ed eseguire funzioni complesse, qualsiasi numero intero può essere rappresentato in binario.
Nella memoria dei dati digitali, nell’archiviazione, nell’elaborazione e nelle comunicazioni, i valori 0 e 1 sono talvolta denominati rispettivamente “livello basso” e “livello alto”.

Il binario può essere utilizzato anche per descrivere programmi software compilati, una volta compilato un programma contiene dati binari chiamati “machine code” che possono essere eseguiti dalla CPU del computer.
Cos'è l'ottale?
L’ottale, abbreviato in OCT o O, è un sistema di conteggio con una base di 8. Utilizza le otto cifre 0, 1, 2, 3, 4, 5, 6, 7, dove dopo 7 si riporta a 0 e si incrementa la cifra più alta di 1. In alcuni linguaggi di programmazione, una cifra iniziale di 0 indica spesso che il numero è in ottale. I numeri ottali e i numeri binari corrispondono su base bit per bit (una cifra ottale corrisponde a tre cifre binarie), rendendo l’ottale utile nei linguaggi informatici.
L’ottale è stato ampiamente utilizzato nei sistemi informatici come PDP-8, ICL 1900 e grandi mainframe IBM, che utilizzano lunghezze di parole di 12 bit, 24 bit o 36 bit. Questi sistemi si basano sull’ottale poiché le loro lunghezze di parole binarie ideali sono multipli di 3 (ogni cifra ottale rappresenta tre cifre binarie). Visualizzare da quattro a dodici cifre in modo conciso rappresenta l’intera macchina. Riduce anche i costi poiché le cifre possono essere visualizzate tramite display digitali, display a sette segmenti e calcolatrici per pannelli di controllo operatore. I display binari sono troppo complessi e i display decimali richiedono hardware complesso, mentre i display esadecimali richiedono la visualizzazione di più cifre.
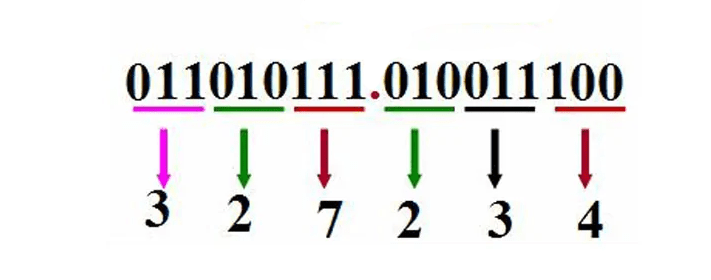
Poiché una cifra esadecimale corrisponde a quattro cifre binarie, l’esadecimale è più conveniente per rappresentare il binario. Pertanto, l’applicazione dell’ottale è meno diffusa dell’esadecimale. Alcuni linguaggi di programmazione forniscono la possibilità di rappresentare i numeri utilizzando la notazione ottale e alcune vecchie applicazioni Unix utilizzano ancora l’ottale. I sistemi informatici richiedono conversioni del sistema numerico internamente, utilizzando il binario come base. Le conversioni del sistema numerico tra binario, ottale e decimale vengono eseguite nella programmazione e FORTRAN77, incentrato su binario e decimale, gestisce queste conversioni.
Tuttavia, tutte le moderne piattaforme di calcolo utilizzano sistemi a 16, 32 o 64 bit, dove le piattaforme a 64 bit si dividono ulteriormente in byte a 8 bit. In questi sistemi, tre cifre ottali soddisfano ogni requisito di byte, con la cifra ottale più significativa che rappresenta due cifre binarie (con +1 per il byte successivo, se applicabile). Rappresentare parole a 16 bit in ottale richiede 6 cifre, ma la cifra ottale più significativa rappresenta solo 1 cifra binaria (0 o 1). Questa limitazione impedisce byte facili da leggere poiché si traducono in cifre ottali a 4 bit.
Di conseguenza, l’esadecimale è ora più comunemente utilizzato nei linguaggi di programmazione, poiché due cifre esadecimali specificano completamente un byte. Le piattaforme con potenze di due e dimensioni delle parole rendono le istruzioni più comprensibili. L’onnipresente architettura x86 è un esempio di ciò, sebbene l’ottale sia raramente utilizzato in questa architettura. Tuttavia, l’ottale può essere utile per descrivere alcune codifiche binarie, come il byte ModRM, che è suddiviso in 2, 3 e 3 bit.
Cos'è il decimale?
Il sistema decimale, spesso indicato come sistema in base 10, è un metodo di conteggio in cui ogni dieci unità portano a un’unità superiore. La prima cifra ha un valore posizionale di 10^0, la seconda cifra 10^1, la N-esima cifra 10^(N-1). Il valore di un numero in questo sistema è la somma del valore di ogni cifra moltiplicato per il suo peso posizionale.
Il metodo di conteggio decimale è il più utilizzato nella vita di tutti i giorni. Presenta un incremento di dieci tra unità adiacenti, formando la base della notazione decimale. Ciò deriva probabilmente dal fatto che gli esseri umani possiedono tipicamente dieci dita, influenzando lo sviluppo dell’aritmetica utilizzando il sistema decimale. Aristotele osservò che gli esseri umani usano generalmente il sistema decimale a causa della realtà anatomica di avere dieci dita.
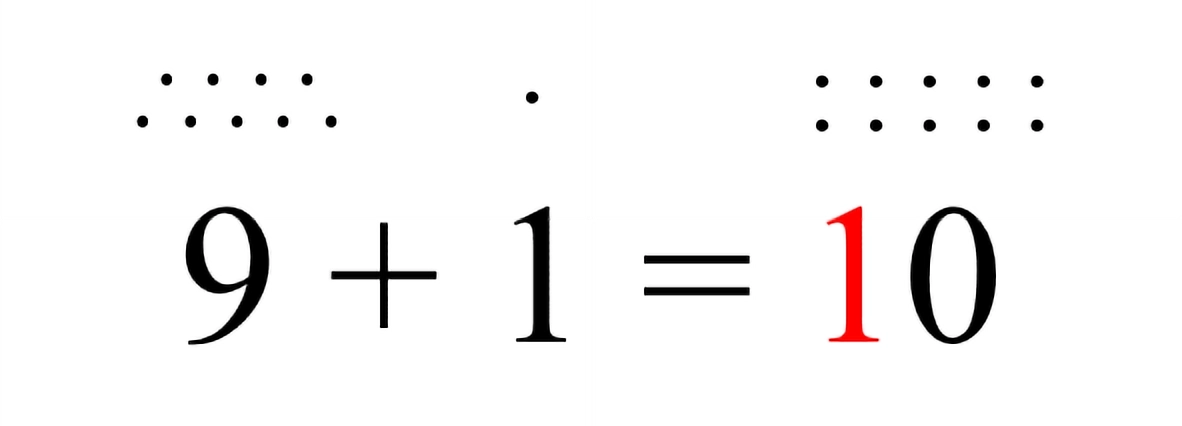
Storicamente, la maggior parte dei sistemi numerali scritti sviluppati in modo indipendente impiegava una base decimale, ad eccezione dei sistemi numerali babilonesi sessagesimali (base-60) e dei sistemi numerali Maya vigesimali (base-20). Tuttavia, questi sistemi decimali non erano necessariamente posizionali.
Il termine “decimale” deriva dalla parola latina “decem”, che significa dieci. Il metodo di conteggio decimale fu inventato dai matematici indù circa 1.500 anni fa e fu successivamente trasmesso dagli arabi nell’XI secolo. Si basa su due principi: la notazione posizionale e la rappresentazione in base dieci. Tutti i numeri sono composti dai dieci simboli di base e, quando un’unità raggiunge dieci, viene riportata alla posizione successiva, rendendo cruciale la posizione di un simbolo. I simboli fondamentali sono le cifre da 0 a 9.
Per rappresentare multipli di dieci, le cifre vengono spostate di una posizione verso sinistra con uno zero finale, ottenendo 10, 20, 30 e così via. Allo stesso modo, i multipli di cento comportano lo spostamento delle cifre ancora una volta: 100, 200, 300 e così via. Per esprimere una frazione di dieci, le cifre vengono spostate verso destra e vengono aggiunti zeri se necessario: 1/10 diventa 0,1, 1/100 diventa 0,01 e 1/1000 diventa 0,001.
Cos'è l'Esadecimale?
L’esadecimale (abbreviato come hex o pedice 16) è un sistema di conteggio con una base di 16, che è un sistema di base in cui ogni 16 viene aggiunto a 1. Solitamente rappresentato dai numeri 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 e dalle lettere A, B, C, D, E, F (a, b, c, d, e, f), tra cui: A~F rappresentano 10~15, questi sono chiamati numeri esadecimali.
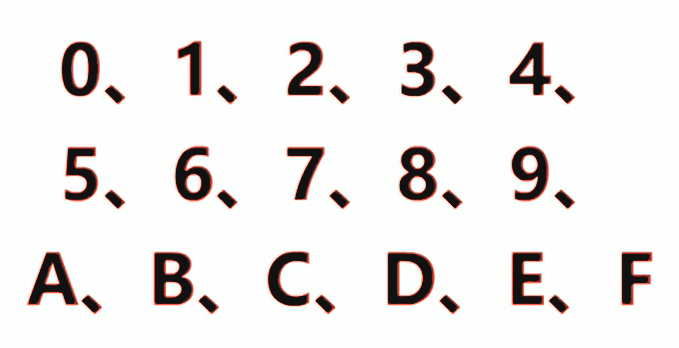
Ad esempio, il numero 57 in decimale è scritto come 111001 in binario e 39 in esadecimale. Il sistema esadecimale odierno è ampiamente utilizzato nel campo informatico, perché non è difficile convertire 4 bit (Bit) in numeri esadecimali individuali. 1 byte può essere rappresentato come 2 numeri esadecimali consecutivi. Tuttavia, questa notazione mista è confusa e richiede alcuni prefissi, suffissi o pedici per mostrarlo.
Decimale a Binario
La conversione di un numero decimale in un numero binario comporta conversioni separate per le parti intere e frazionarie, che vengono poi combinate.
Per la parte intera, si utilizza il metodo della “divisione per 2 e inversione dei resti”. La procedura è la seguente: dividere il numero decimale intero per 2, ottenendo un quoziente e un resto. Dividere nuovamente il quoziente per 2 e continuare questo processo finché il quoziente non diventa inferiore a 1. Quindi, prendere i resti inizialmente ottenuti come bit meno significativi del numero binario e i resti successivamente ottenuti come bit più significativi, disponendoli in ordine inverso.
| Decimal | Binary |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
Ad esempio, convertendo il numero decimale 1 in binario si ottiene 1B (dove B indica il suffisso binario). Per il numero decimale 2, poiché raggiungiamo 2, dobbiamo riportare 1, ottenendo il numero binario 10B. Allo stesso modo, quando si converte il numero decimale 5 in binario, poiché 2 è 10B, allora 3 è 10B + 1B = 11B, 4 è 11B + 1B = 100B e 5 è 100B + 1B = 101B. Continuando questo schema, quando il numero decimale è 254, la sua rappresentazione binaria è 11111110B.
Possiamo dedurre una regola generale quando si convertono i numeri binari in numeri decimali. Partendo dal bit meno significativo del numero binario e procedendo all’indietro, ogni bit rappresenta 2 elevato alla potenza di n, dove n indica la posizione del bit dalla fine. Qui, n inizia a contare da 0. Se un bit binario ha un valore di 1, contribuisce alla somma; se è 0, non contribuisce. Ad esempio, ricaviamo il numero decimale dal numero binario 11111110B, seguendo il processo di calcolo:
0*20+1*21+1*22+1*23+1*24+1*25+1*26+1*27=254
Perché i computer usano il sistema binario?
Innanzitutto, il sistema numerico binario utilizza solo due cifre. 0 e 1, quindi qualsiasi elemento con due stati stabili diversi può essere utilizzato per rappresentare un certo bit di un numero. In effetti, ci sono molti componenti con due stati stabili distinti. Ad esempio, “on” e “off” di una lampada al neon; “on” e “off” di un interruttore; “high” e “low”, “positivo” e “negativo” di una tensione; “Nessun foro”; “segnale” e “nessun segnale” nel circuito; poli sud e nord di materiali magnetici, ecc., la lista continua. Utilizzare questi stati distinti per rappresentare i numeri è facile da implementare. Non solo, ma soprattutto, i due stati completamente diversi non sono solo quantitativamente diversi, ma anche qualitativamente diversi. In questo modo, la capacità anti-interferenza della macchina può essere notevolmente migliorata e l’affidabilità può essere migliorata. È molto più difficile trovare un dispositivo semplice e affidabile che possa rappresentare più di due stati.
In secondo luogo, le quattro regole aritmetiche del sistema di conteggio binario sono molto semplici. Inoltre, tutte e quattro le operazioni aritmetiche possono essere ricondotte all’addizione e allo spostamento alla fine, in modo che il circuito dell’unità aritmetica nel computer elettronico sia diventato molto semplice. Non solo, ma la linea è semplificata e la velocità può essere aumentata. Questo è anche incomparabile con il sistema di conteggio decimale.
In terzo luogo, l’uso di rappresentazioni binarie nei computer elettronici può risparmiare apparecchiature. Può essere dimostrato teoricamente che l’uso del sistema ternario consente di risparmiare più apparecchiature, seguito dal sistema binario. Tuttavia, poiché il sistema binario ha vantaggi che altri sistemi binari inclusi il sistema ternario non hanno, la maggior parte dei computer elettronici utilizza ancora il sistema binario. Inoltre, poiché nel sistema binario vengono utilizzati solo due simboli “0” e “1”, l’algebra booleana può essere utilizzata per analizzare e sintetizzare i circuiti logici nella macchina. Questo fornisce uno strumento utile per la progettazione di circuiti di computer elettronici. In quarto luogo, i simboli binari “1” e “0” corrispondono esattamente a “vero” e “falso” nelle operazioni logiche, il che è conveniente per i computer per eseguire operazioni logiche.
Decimale contro binario contro esadecimale
Esadecimale è simile al binario, con la differenza fondamentale che l’esadecimale segue un sistema “a base sedici”, dove ogni sedici conteggi sono raggruppati insieme. Un altro aspetto importante da notare è che i numeri decimali da 0 a 15 sono rappresentati in esadecimale come da 0 a 9, seguiti da A, B, C, D, E, F, dove 10 in decimale corrisponde ad A in esadecimale, 11 a B, e così via fino a 15 che corrisponde a F.
Generalmente denotiamo i numeri esadecimali aggiungendo il suffisso ‘H’ alla fine, indicando che il numero è in formato esadecimale, come AH, DEH, ecc. La distinzione tra maiuscole e minuscole qui non è significativa. Nel contesto della programmazione nel linguaggio C, i numeri esadecimali dovrebbero essere scritti come “0xA” o “0xDE”, dove il prefisso “0x” indica l’esadecimale.
La conversione tra numeri decimali ed esadecimali non viene discussa qui, poiché le regole sono simili alla conversione tra decimale e binario. È fondamentale essere competenti nella conversione tra decimale, binario ed esadecimale, poiché queste competenze sono ampiamente utilizzate, soprattutto nella programmazione di microcontrollori utilizzando C.
Per i numeri compresi tra 0 e 15, che sono frequentemente utilizzati nella programmazione di microcontrollori, la conversione tipica prevede prima la conversione da binario a decimale, quindi da decimale a esadecimale. Se trovi difficile ricordare queste conversioni ora, puoi rafforzare la tua memoria man mano che progredisci nei tuoi studi.
Ecco la tabella di conversione per i numeri binari, decimali ed esadecimali da 0 a 15:
| Decimal | Binary | Hexadecimal |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |