Was ist ein RLC-Schaltkreis?
Ein RLC-Schaltkreis ist ein elektrischer Schaltkreis, der einen Widerstand (R), eine Induktivität (L) und einen Kondensator (C) enthält, die in Reihe oder parallel geschaltet sind. Diese Komponenten arbeiten zusammen, um Energie zu speichern und zu übertragen, was zu Schwingungen bei einer bestimmten Resonanzfrequenz führt. RLC-Schaltkreise werden häufig in verschiedenen Anwendungen eingesetzt, darunter Filter, Oszillatoren und Abstimmschaltungen.
Arten von RLC-Schaltungen
RLC-Schaltungen lassen sich hauptsächlich in folgende Typen unterteilen:
RLC-Serienkreis:
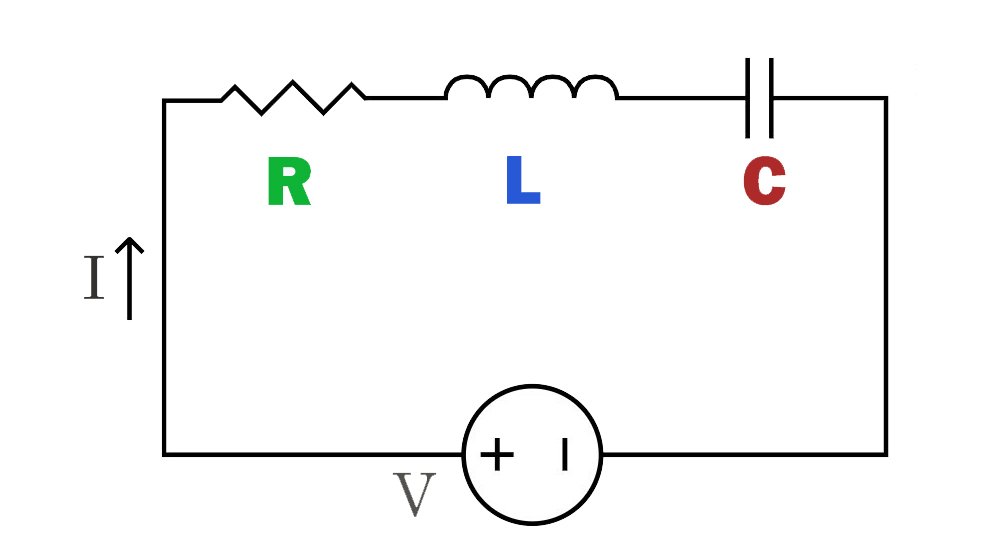
In diesem Schaltkreis sind die Komponenten Widerstand (R), Induktivität (L) und Kondensator (C) nacheinander auf demselben Pfad geschaltet. Der Strom fließt nacheinander durch den Widerstand, die Induktivität und den Kondensator, wodurch sich der Strom in jeder Komponente entsprechend ändert.
Der RLC-Serienschaltkreis hat die Eigenschaft der Frequenzselektivität und weist bei verschiedenen Frequenzen unterschiedliche Impedanz- und Ansprechcharakteristiken auf, weshalb er häufig in Filtern und abgestimmten Schaltkreisen verwendet wird.
RLC-Parallelschaltung:
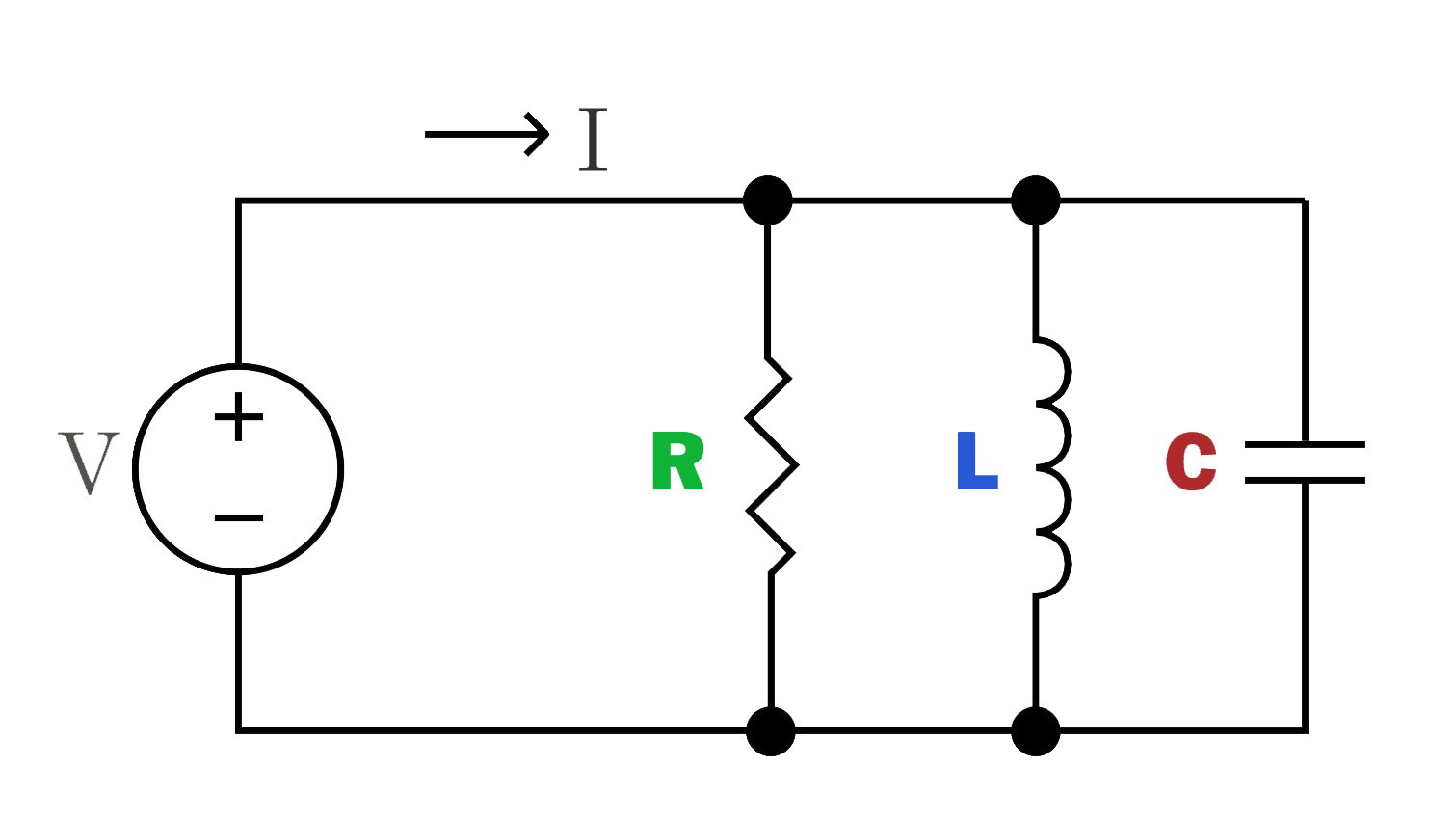
Der parallele RLC-Schaltkreis verbindet den Widerstand, die Induktivität und den Kondensator jeweils in parallelen Pfaden. Der Strom wird auf die Zweige aufgeteilt, und die Spannung, die durch jede Komponente fließt, ist gleich.
Der Schaltkreis hat Impedanzeigenschaften für Strom bei einer bestimmten Frequenz, die dazu verwendet werden können, Signale bestimmter Frequenzen selektiv durchzulassen oder zu blockieren.
Wie misst man die Spannung in einem RLC-Stromkreis?
Wie die folgenden Diagramme zeigen:
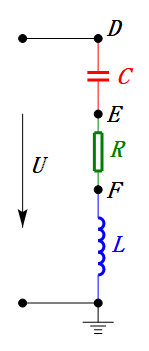
Wenn U eine sinusförmige Spannung ist, hat dieser Stromkreis drei Potentialpunkte D, E und F. Diese drei Wellenformen können mit einem Oszilloskop beobachtet oder mit einem Wechselspannungsmessgerät für UD, UE, UL, UR und UC gemessen werden. Das dynamische Diagramm auf der rechten Seite spiegelt die Veränderungen dieser fünf Spannungen im Laufe der Zeit in einem bestimmten Szenario wider. Im dynamischen Diagramm entspricht UF UL, und idealerweise sollte es eine weitere Spannung UDF geben, aber ich habe mich der Einfachheit halber dafür entschieden, Spannungen mit zweistelligen Indizes nicht aufzunehmen.
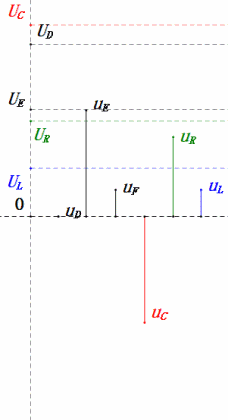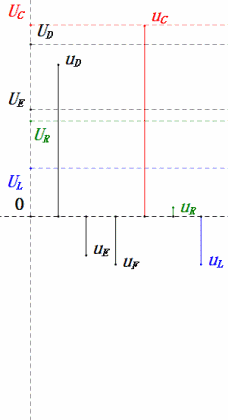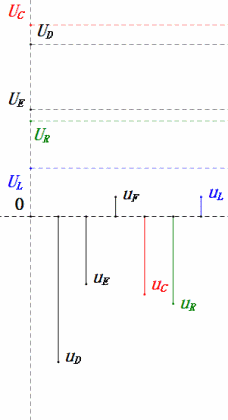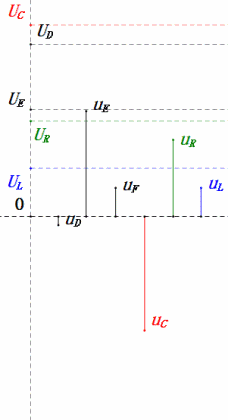
Berechnungsformel für Spannung
Die Zeigermethode ist eine brillante Lösung, die die Problemlösung erleichtert, aber dazu führen kann, dass wir die faszinierenden dynamischen Prozesse übersehen, die in der obigen Grafik dargestellt sind. Mit der induktiven Reaktanz XL, dem Widerstand R und der kapazitiven Reaktanz XC lässt sich die Zeigermethode zur Lösung dieses Schaltkreises wie folgt zusammenfassen:
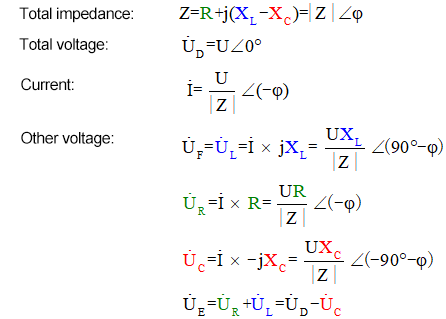
Das Wechselspannungsmessgerät misst UR ≠ UE – UL. Wenn L ein idealer Induktor ist, bilden diese drei ein rechtwinkliges Dreieck. In ähnlicher Weise bilden UC, UD und UE ebenfalls ein Dreieck, wenn auch nicht unbedingt ein rechtwinkliges. Dies bedeutet nicht, dass das Kirchhoffsche Spannungsgesetz (KVL) verletzt wird. Wenn der Momentanwert u zu einem bestimmten Zeitpunkt gemessen wird, ergibt sich uR = uE – uL und uC = uD – uE. Obwohl der Strom nicht gemessen wird, sind die Änderungen von UR phasengleich mit den Änderungen des Stroms.
Sinusförmiges Signal und Resonanzzustand
Wenn ein Sinussignal angelegt wird, beträgt die induktive Reaktanz XL = ωL und die kapazitive Reaktanz XC = (ωC)^-1. Der Zustand, in dem diese beiden Werte gleich sind, wird als Resonanz bezeichnet und ermöglicht die Berechnung einer Resonanzwinkelgeschwindigkeit ω0.
Im nächsten Abschnitt legen wir die Parameter fest, um Zeigerdiagramme, statische Sinuswellen-Diagramme und Animationen der momentanen Wertänderungen der Spannung bei 0,5ω0, ω0 und 2ω0 zu erstellen.
Spannung bei verschiedenen Resonanzwinkel-Frequenzen
Modellparameter:
- U = 6,00 mV
- R = 2,00 Ω (effektiver Strom weniger als 3,00 mA, im Allgemeinen sicher für Komponenten)
- C = 125 μF
- L = 0,500 mH
Berechnetes ω0 = 4000 rad/s (entspricht einer Frequenz von ca. 637 Hz, wobei elektromagnetische Strahlungseffekte zur Vereinfachung der Modellierung vernachlässigt werden. Phasendiagramme und Sinuswellendiagramme verwenden RMS-Werte; für Spitzenwerte multiplizieren Sie mit 1,414)
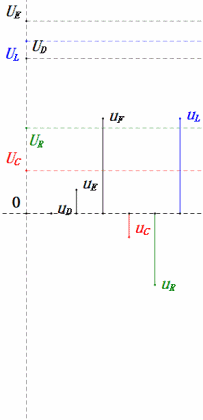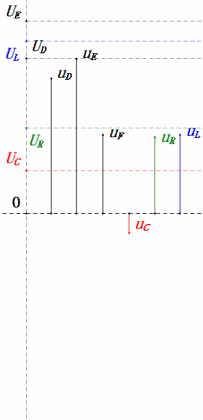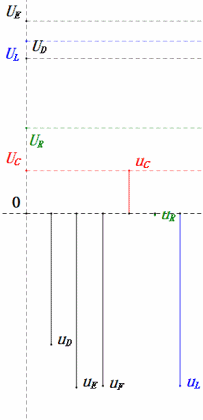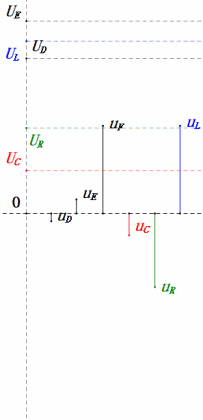
Dynamische Spannung unter 0,5 ω0
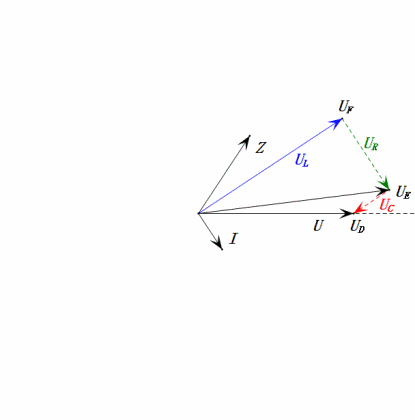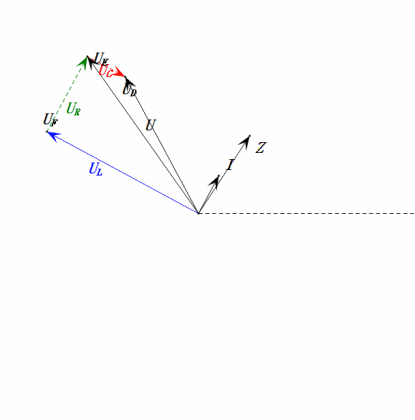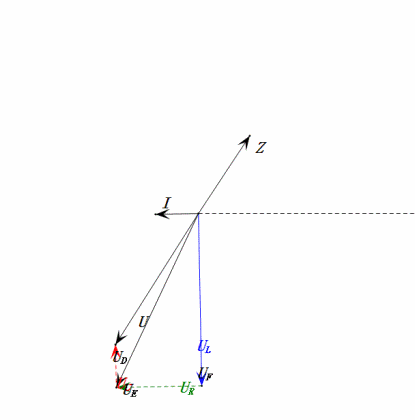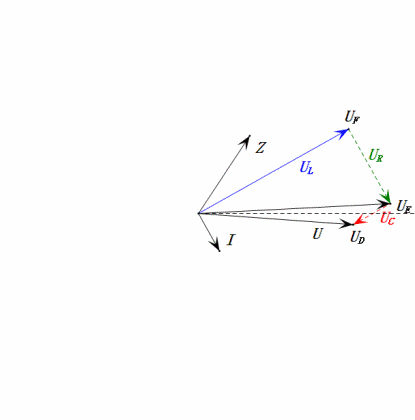
Nach den Berechnungen können wir das Zeigerdiagramm und das statische Sinuswellen-Diagramm zum Anfangszeitpunkt zeichnen:
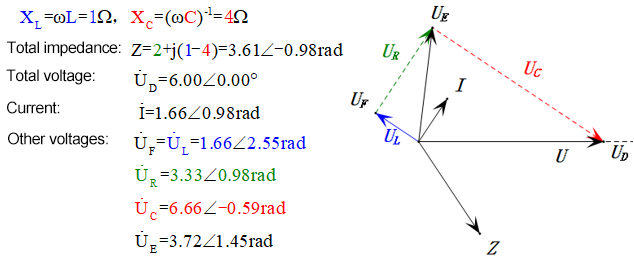
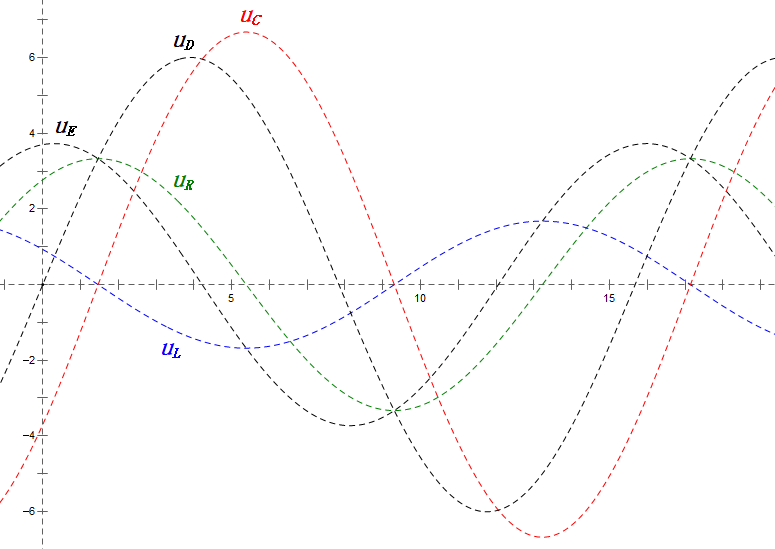
Analyse:
- Maximaler Strom ≈ 1,57 mA, sicher für Komponenten.
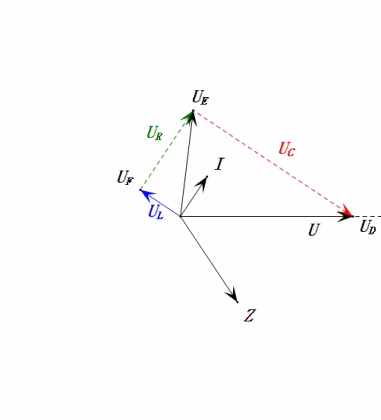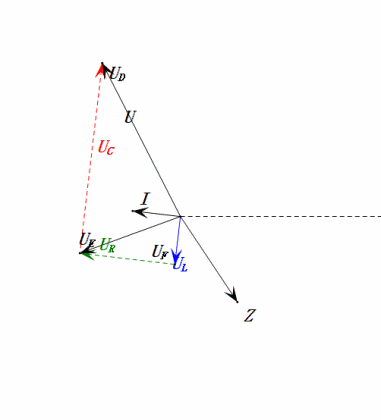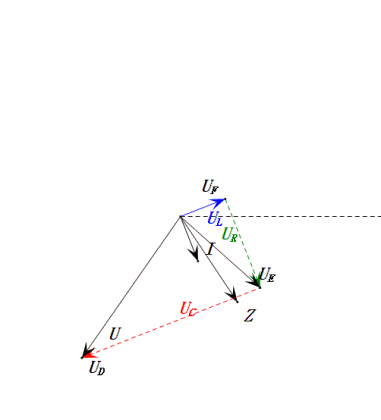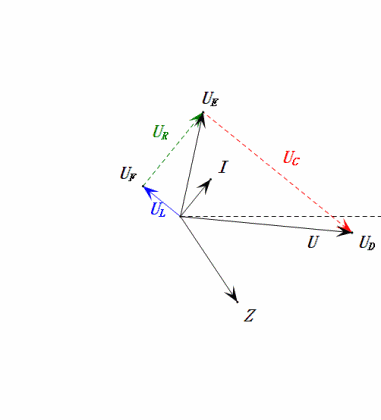
- Das Phasendiagramm bildet ein rechtwinkliges Trapez, wobei UDF nicht berücksichtigt wird.
- Bei 0,5 ω0 ist XL < XC → kleinerer UL, größerer UC. Der maximale uC überschreitet die Versorgungsspannung, wodurch der Kondensator beschädigt werden kann.
- uC liegt um ≈30° hinter uD zurück; der Ladevorgang beginnt während der Anstiegsphase von uD und endet, wenn uR = 0 ist.
- Das Sinusdiagramm zeigt uR = uE – uL und uC = uD – uE zu jedem Zeitpunkt.
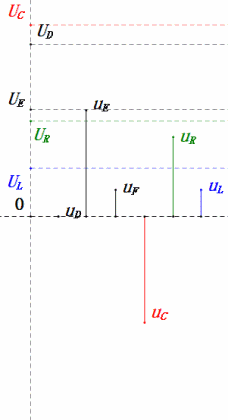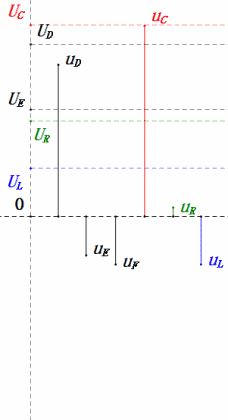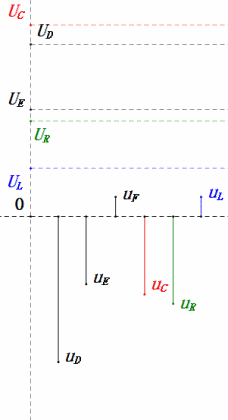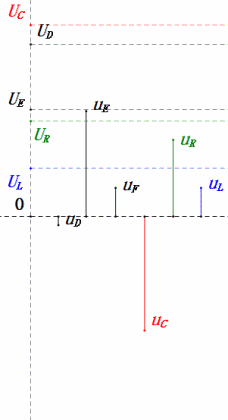
Dynamische Spannung unter 1ω0
Nach den Berechnungen können wir das Zeigerdiagramm und das statische Sinuswellen-Diagramm zum Anfangszeitpunkt zeichnen:
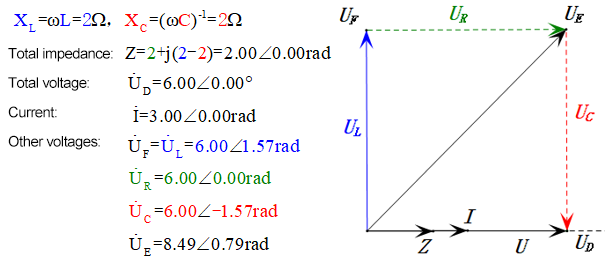
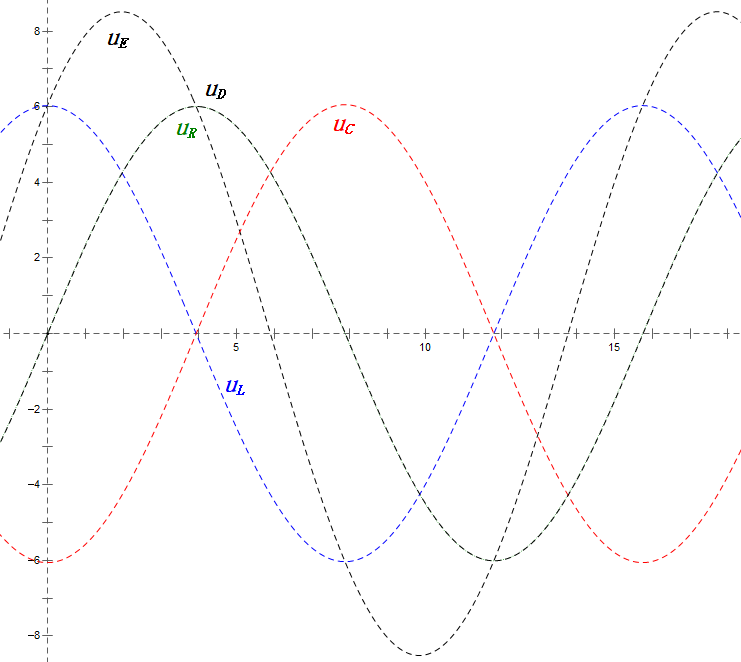
Analyse:
- Maximaler Strom ≈ 4,24 mA, sicher für Komponenten.
- Das Phasendiagramm bildet bei Resonanz (XL = XC) ein Quadrat.
- Maximale uE überschreitet die Versorgungsspannung, aber Auswirkungen auf die Komponenten unklar.
- Zufall: XL = XC = R → uL und uC heben sich im Sinusdiagramm gegenseitig auf, aber Stromänderungen beeinflussen die Amplituden.
- Impedanz minimiert, Strom maximiert bei Resonanz aufgrund des „Maximalstrom”-Effekts.
- uC liegt genau 90° hinter uD zurück; der Ladevorgang beginnt, wenn uD seinen Spitzenwert erreicht, und endet, wenn uR = uD = 0 ist.
- Die Segmente des Sinusdiagramms entsprechen der Hälfte der Zeit von Fall 1.
- Maximales UD = UR, UL = UC aufgrund der Parameter, aber dass alle vier Spannungen gleich sind, ist ein Zufall.
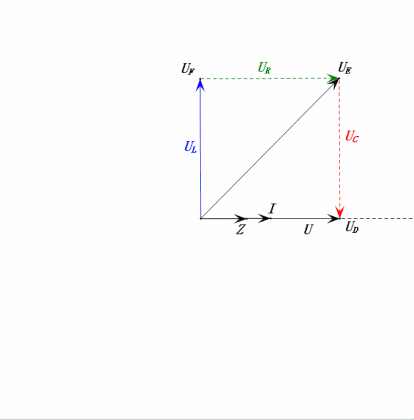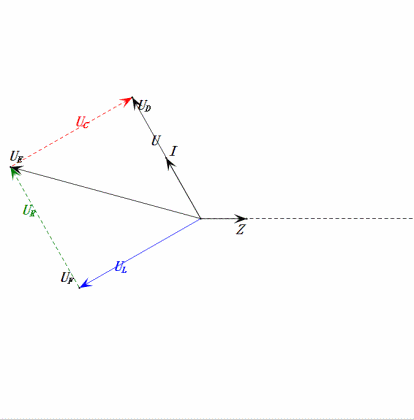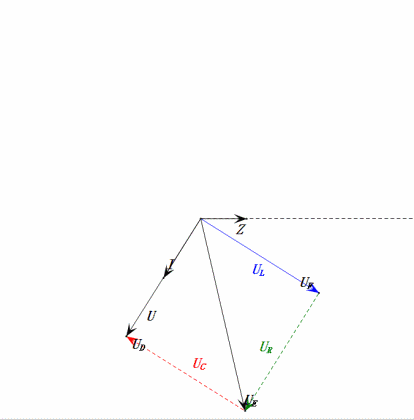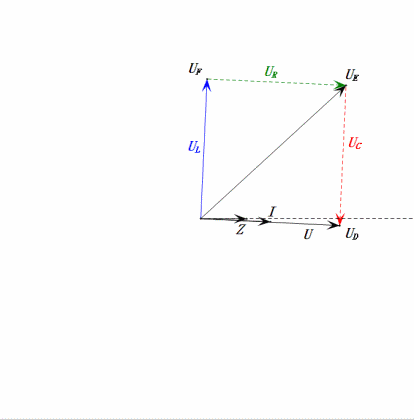
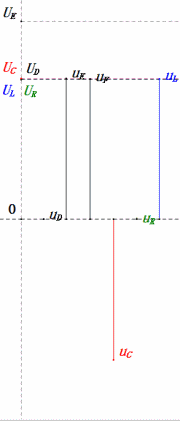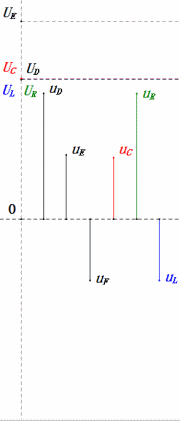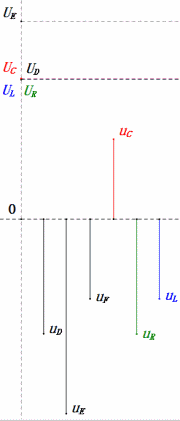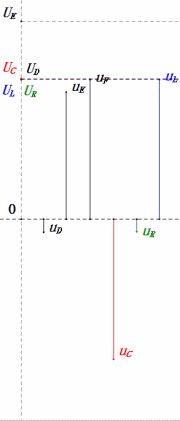
Dynamische Spannung unter 2ω0
Nach den Berechnungen können wir das Zeigerdiagramm und das statische Sinuswellen-Diagramm zum Anfangszeitpunkt zeichnen:
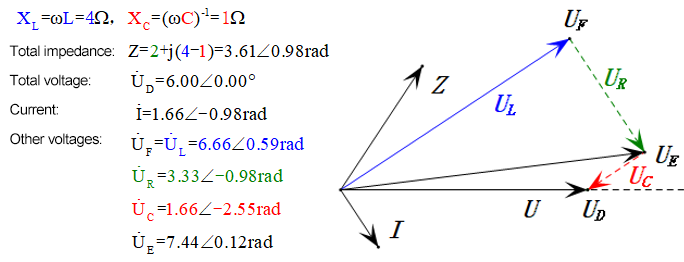
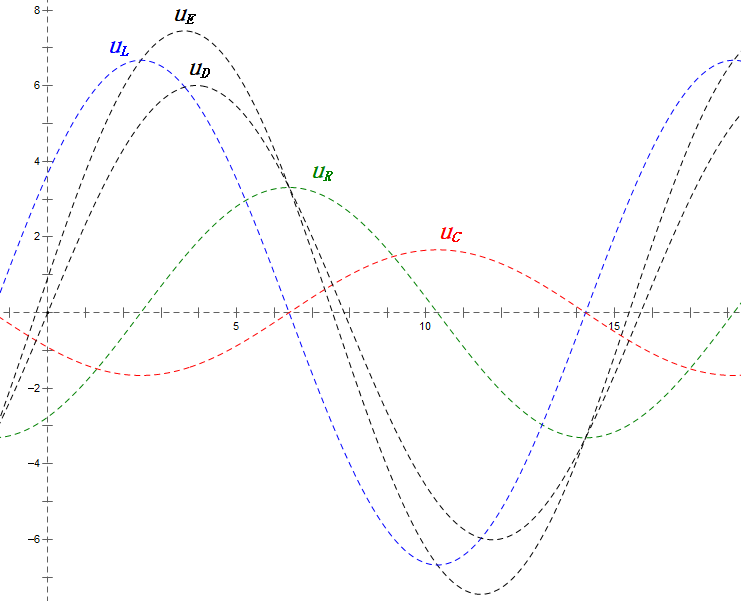
Analyse:
- Maximaler Strom ≈ 1,57 mA, sicher für Komponenten.
- Das Phasendiagramm bildet ein rechtwinkliges Trapez.
- Bei 2ω0 ist XL > XC → größeres UL, kleineres UC. Maximale uL und uE überschreiten die Versorgungsspannung, was zu Bedenken hinsichtlich einer Beschädigung der Induktivität führt.
- uC liegt um ≈150° hinter uD zurück; der Ladevorgang beginnt, wenn uD auf ≈die Hälfte seines Maximums fällt, und endet, wenn uR = uD = 0 ist.
- Die Segmente des Sinusdiagramms entsprechen der Hälfte der Zeit von Fall 2.
- Die Gleichungen uR = uE – uL und uC = uD – uE gelten zu jedem Zeitpunkt.