Che cos'è un circuito RLC?
Un circuito RLC è un circuito elettrico che contiene una resistenza (R), un induttore (L) e un condensatore (C) collegati in serie o in parallelo. Questi componenti lavorano insieme per immagazzinare e trasferire energia, portando a oscillazioni a una specifica frequenza di risonanza. I circuiti RLC sono comunemente utilizzati in varie applicazioni, tra cui filtri, oscillatori e circuiti di sintonizzazione.
Tipi di circuiti RLC
I circuiti RLC possono essere suddivisi principalmente nei seguenti tipi:
Circuito RLC in serie:
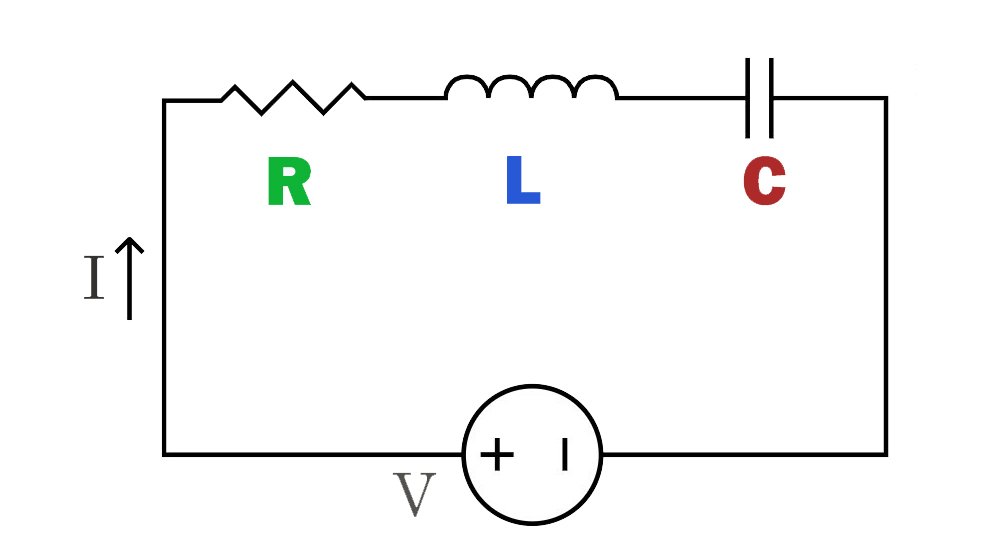
In questo circuito, i componenti resistenza (R), induttore (L) e condensatore (C) sono collegati in sequenza sullo stesso percorso. La corrente passa attraverso la resistenza, l’induttore e il condensatore in sequenza, causando la variazione della corrente in ciascun componente.
Il circuito RLC in serie ha le caratteristiche di selettività di frequenza, presentando diverse impedenze e caratteristiche di risposta a diverse frequenze, quindi è ampiamente utilizzato in filtri e circuiti sintonizzati.
Circuito RLC in parallelo:
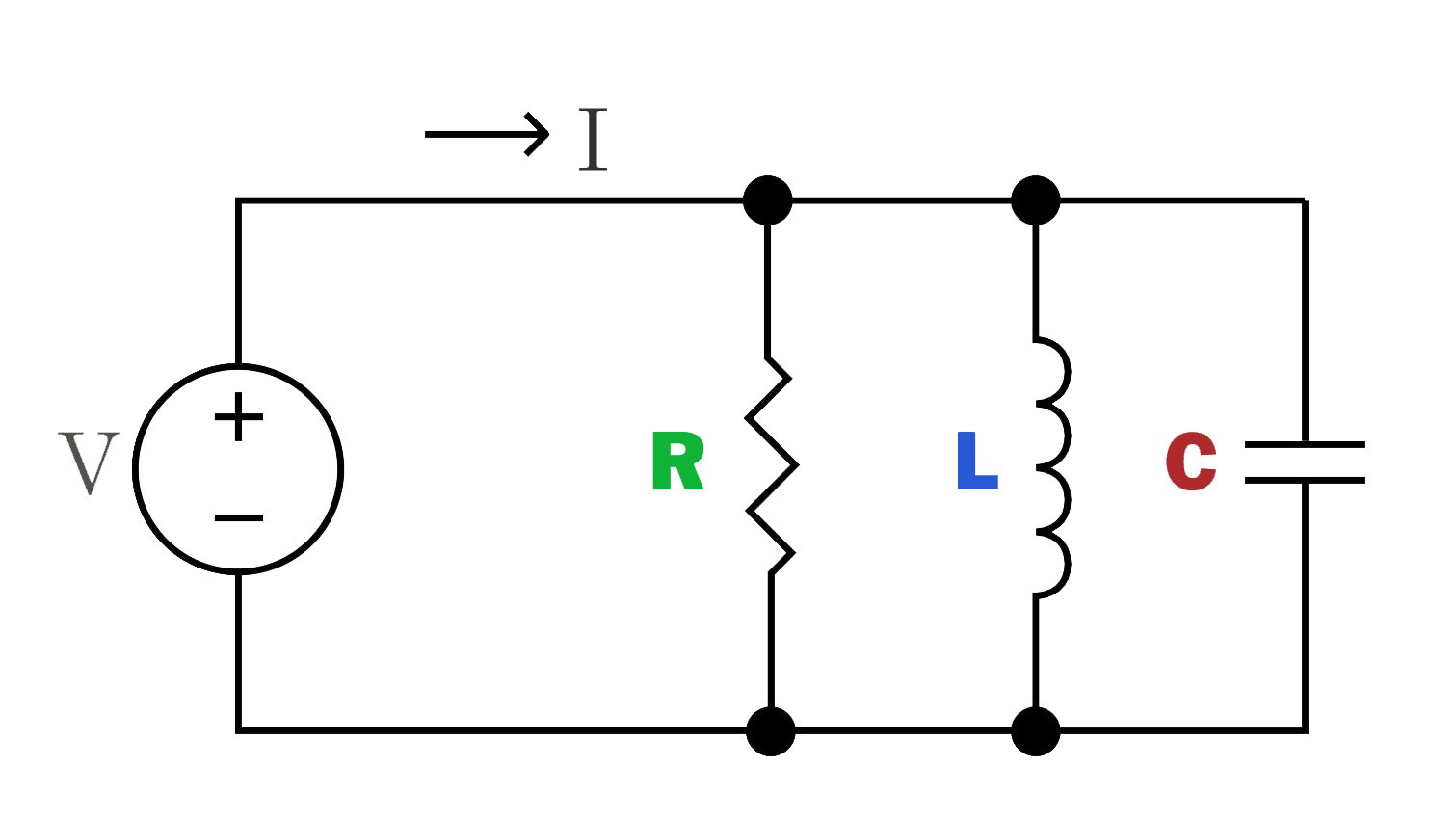
Il circuito RLC in parallelo consiste nel collegare la resistenza, l’induttore e il condensatore in percorsi paralleli rispettivamente. La corrente è divisa nei rami e la tensione che passa attraverso ciascun componente è la stessa.
Il circuito ha caratteristiche di impedenza per la corrente a una specifica frequenza, che può essere utilizzata per passare o bloccare selettivamente segnali di determinate frequenze.
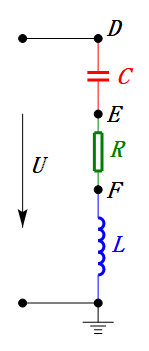
Come misurare la tensione nel circuito RLC?
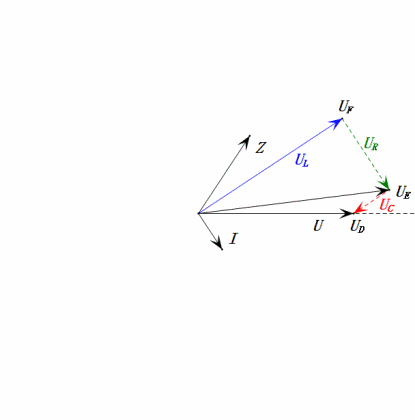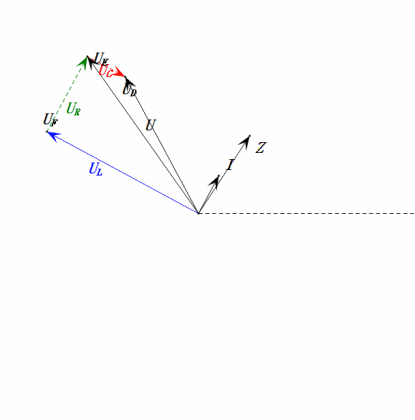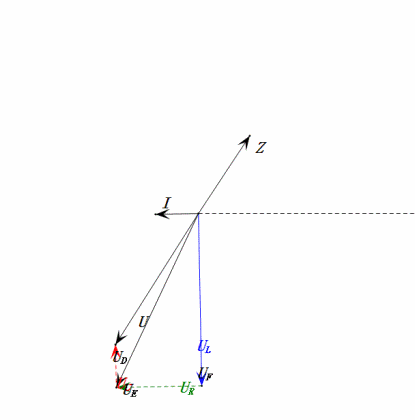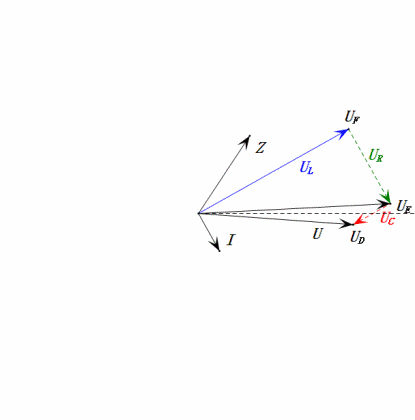
Come mostrano i diagrammi seguenti:
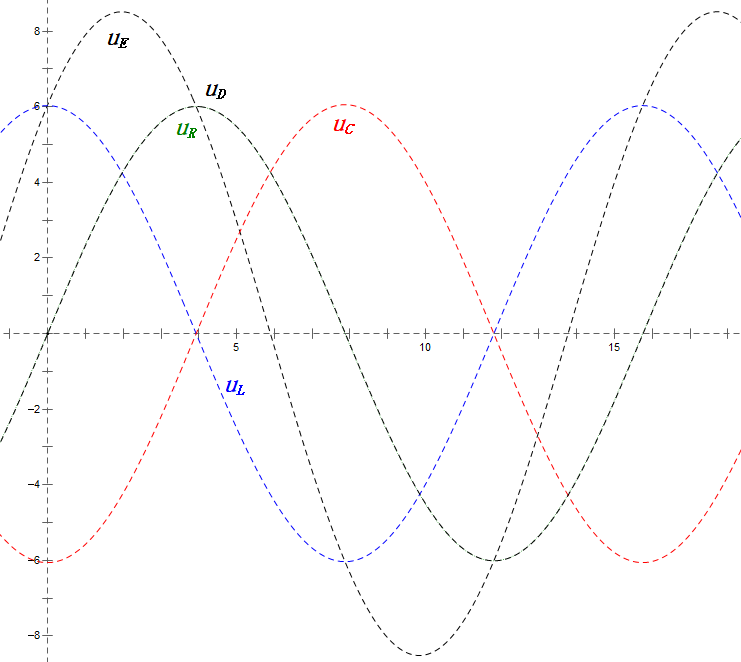
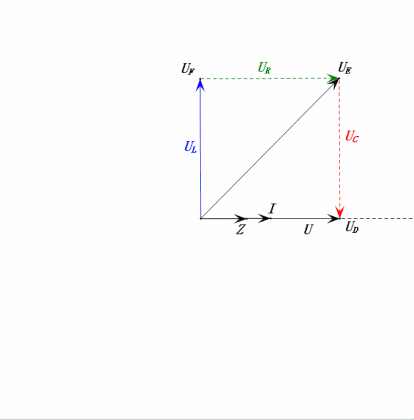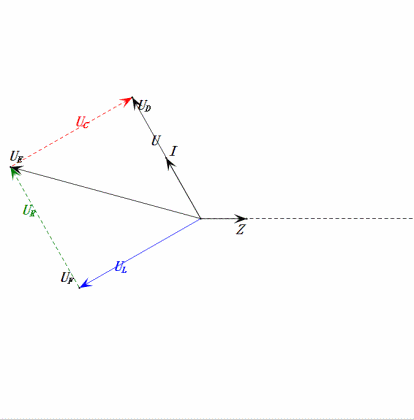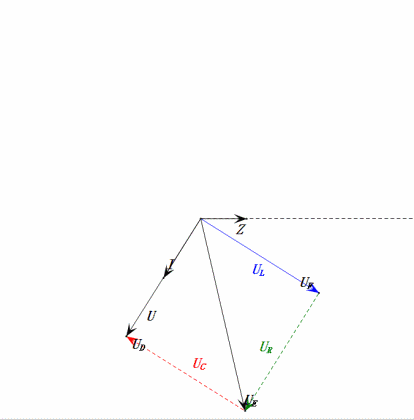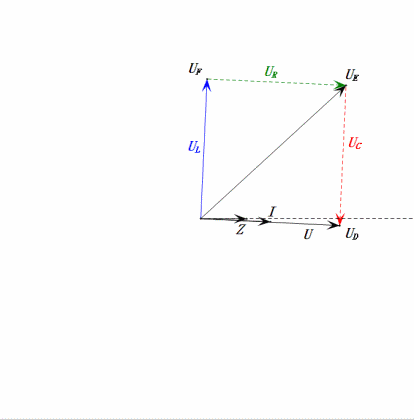
Quando U è una tensione sinusoidale, questo circuito ha tre punti potenziali D, E e F. Queste tre forme d’onda possono essere osservate utilizzando un oscilloscopio o misurate con un voltmetro CA per UD, UE, UL, UR e UC. Il grafico dinamico a destra riflette le variazioni di queste cinque tensioni nel tempo in uno scenario specifico. Nel grafico dinamico, UF è equivalente a UL e idealmente dovrebbe esserci un’altra tensione UDF, ma ho scelto di non includere tensioni con sottoscrizioni di due lettere per semplicità.
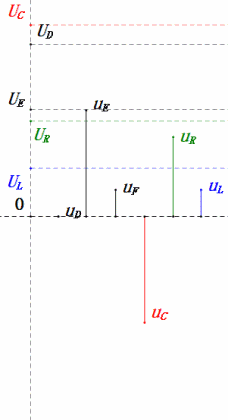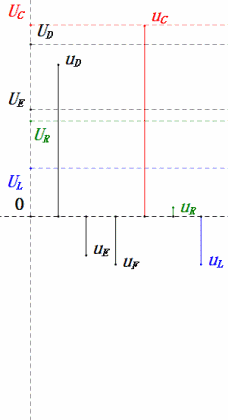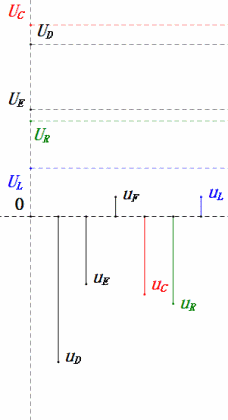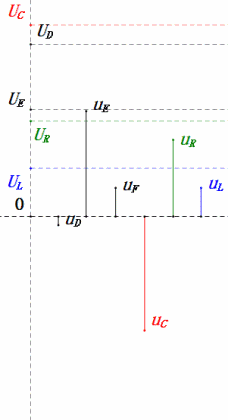
Formula di calcolo per la tensione
Il metodo fasoriale è una soluzione brillante che facilita la risoluzione dei problemi, ma potrebbe farci perdere i fascinanti processi dinamici rappresentati nel grafico precedente. Con la reattanza induttiva XL, la resistenza R e la reattanza capacitiva XC, il metodo fasoriale per risolvere questo circuito è delineato come segue:
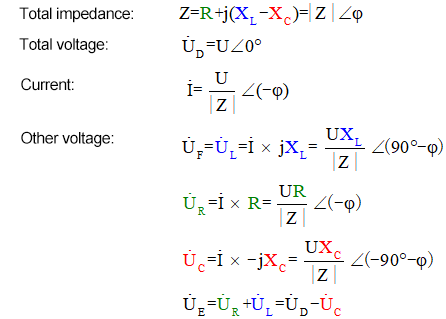
Il voltmetro CA misura UR ≠ UE – UL. Se L è un induttore ideale, questi tre formeranno un triangolo rettangolo. Allo stesso modo, UC, UD e UE formeranno anche un triangolo, anche se non necessariamente un triangolo rettangolo. Ciò non implica una violazione della legge di Kirchhoff sulla tensione (KVL). Se il valore istantaneo u in un determinato momento viene misurato, si troverà che uR = uE – uL e uC = uD – uE. Inoltre, anche se la corrente non viene misurata, le variazioni di UR sono in fase con le variazioni di corrente.
Azione del segnale sinusoidale e stato di risonanza
Quando viene applicato un segnale sinusoidale, la reattanza induttiva XL = ωL e la reattanza capacitiva XC = (ωC)^-1. Lo stato in cui queste due sono uguali è noto come risonanza, consentendoci di calcolare una frequenza angolare di risonanza ω0.
Nella sezione successiva, imposteremo i parametri per creare diagrammi fasoriali, diagrammi di onde sinusoidali statiche e animazioni delle variazioni istantanee del valore della tensione a 0,5ω0, ω0 e 2ω0.
Tensione a diverse frequenze angolari di risonanza
Parametri del modello:
- U = 6,00mV
- R = 2,00Ω (corrente efficace inferiore a 3,00mA, generalmente sicura per i componenti)
- C = 125μF
- L = 0,500mH
ω0 calcolato = 4000rad/s (corrispondente a una frequenza di circa 637Hz, ignorando gli effetti della radiazione elettromagnetica per comodità di modellazione. I diagrammi fasoriali e i diagrammi di onde sinusoidali utilizzano valori RMS; per i valori di picco, moltiplicare per 1,414)
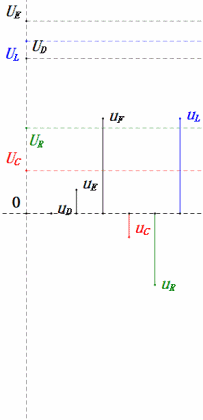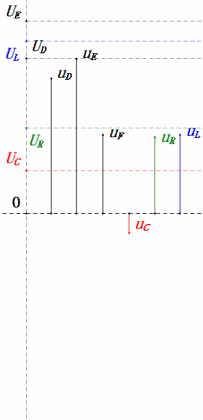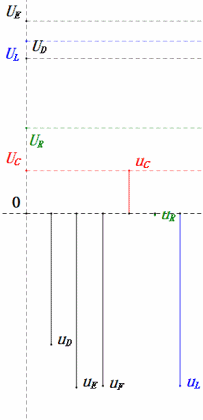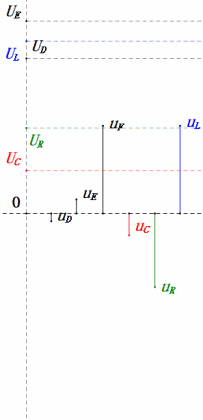
Tensione dinamica a 0,5ω0
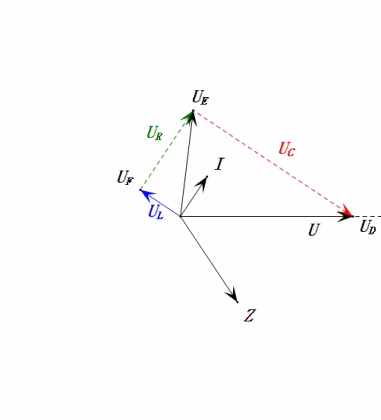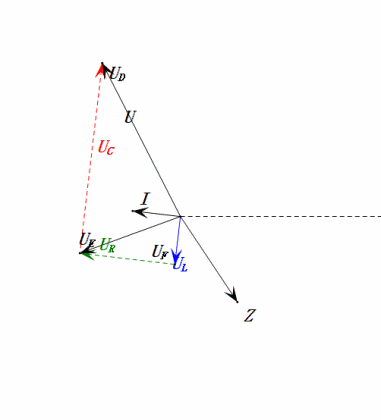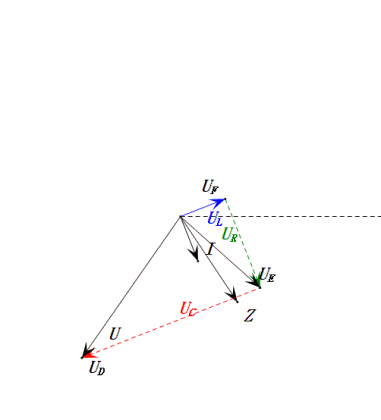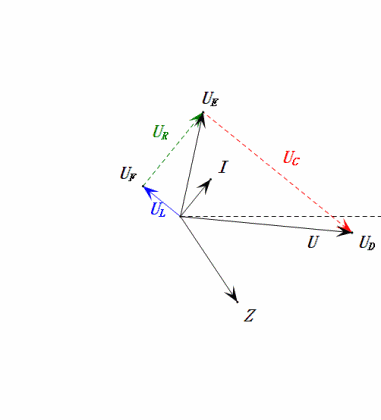
Dopo i calcoli, possiamo disegnare il diagramma fasoriale e il diagramma della sinusoide statica all’istante iniziale:
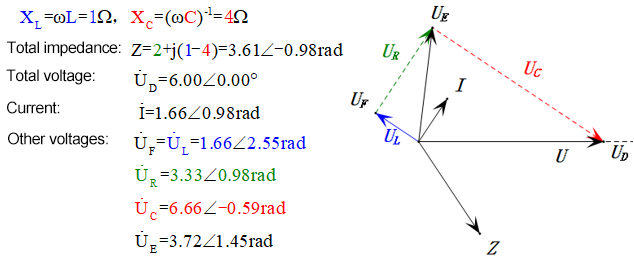
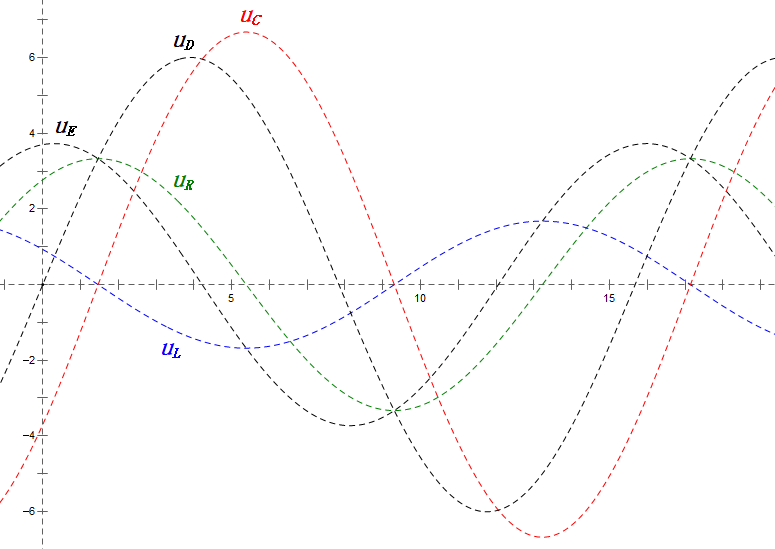
Analisi:
- Corrente massima ≈ 1,57mA, sicura per i componenti.
- Il diagramma fasoriale forma un trapezio rettangolo con UDF non considerato.
- A 0,5π, XL < XC ⇒ UL più piccola, UC più grande. UC massima supera la tensione di alimentazione, danneggiando potenzialmente il condensatore.
- uC è in ritardo di circa 30° rispetto a uD; la carica inizia durante la fase crescente di uD, terminando quando uR = 0.
- Il diagramma della sinusoide mostra uR = uE – uL e uC = uD – uE ad ogni istante.
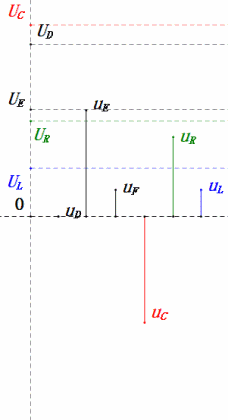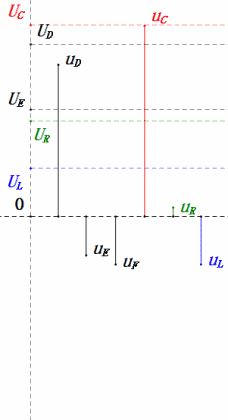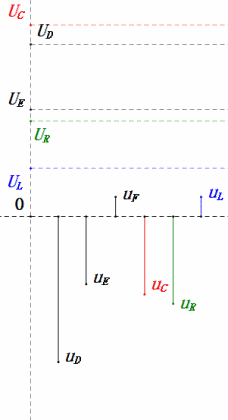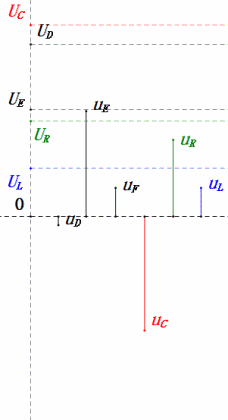
Tensione dinamica sotto 1π
Dopo i calcoli, possiamo disegnare il diagramma fasoriale e il diagramma della sinusoide statica all’istante iniziale:
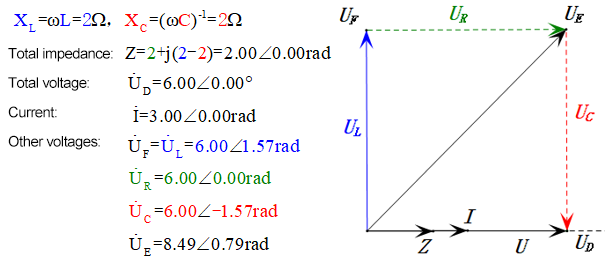
Analisi:
- Corrente massima ≈ 4,24mA, sicura per i componenti.
- Il diagramma fasoriale forma un quadrato in risonanza (XL = XC).
- uE massima supera la tensione di alimentazione, ma l’impatto sui componenti non è chiaro.
- Coincidenza: XL = XC = R ⇒ uL e uC si annullano a vicenda nel diagramma della sinusoide, ma le variazioni di corrente influiscono sulle ampiezze.
- L’impedenza è minimizzata, la corrente è massimizzata in risonanza grazie all’effetto “corrente massima”.
- uC è in ritardo di esattamente 90° rispetto a uD; la carica inizia quando uD raggiunge il picco e termina quando uR = uD = 0.
- I segmenti del diagramma della sinusoide rappresentano metà del tempo del Caso 1.
- UD massima = UR, UL = UC a causa dei parametri, ma il fatto che tutte e quattro le tensioni siano uguali è una coincidenza.
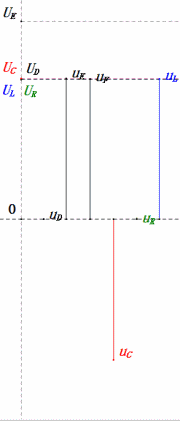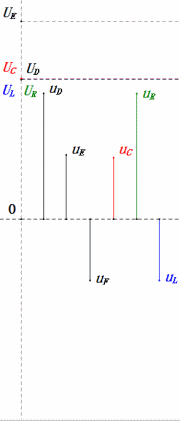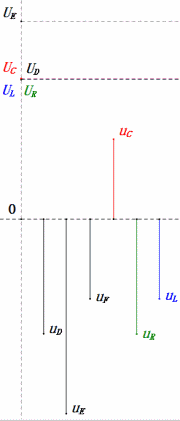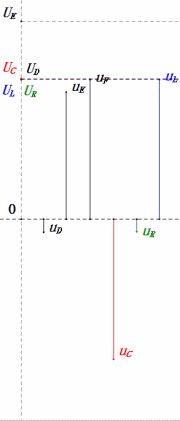
Tensione dinamica sotto 2π
Dopo i calcoli, possiamo disegnare il diagramma fasoriale e il diagramma della sinusoide statica all’istante iniziale:
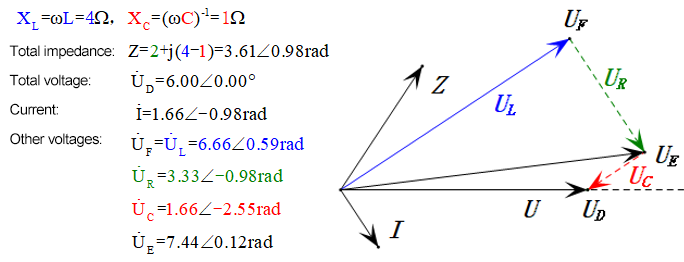
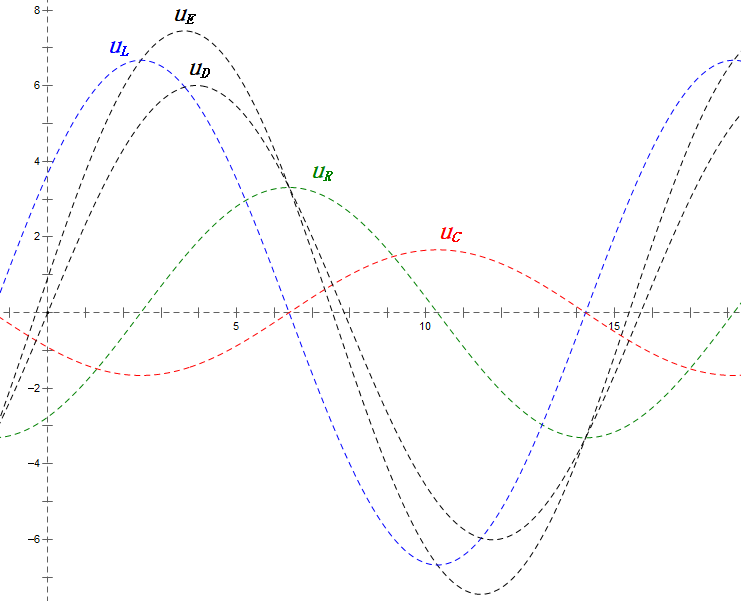
Analisi:
- Corrente massima ≈ 1,57mA, sicura per i componenti.
- Il diagramma fasoriale forma un trapezio rettangolo.
- A 2π, XL > XC ⇒ UL più grande, UC più piccola. UL e uE massimi superano la tensione di alimentazione, sollevando preoccupazioni per danni all’induttore.
- uC è in ritardo di circa 150° rispetto a uD; la carica inizia quando uD scende a circa metà del suo massimo, terminando quando uR = uD = 0.
- I segmenti del diagramma della sinusoide rappresentano metà del tempo del Caso 2.
- Le equazioni uR = uE – uL e uC = uD – uE sono valide ad ogni istante.