Qué es un circuito RLC?
Un circuito RLC es un circuito eléctrico que contiene una resistencia (R), un inductor (L) y un capacitor (C) conectados en serie o paralelo. Estos componentes trabajan juntos para almacenar y transferir energía, lo que lleva a oscilaciones a una frecuencia resonante específica. Los circuitos RLC se utilizan comúnmente en varias aplicaciones, incluidas filtros, osciladores y circuitos de sintonización.
Tipos de Circuitos RLC
Los circuitos RLC se pueden dividir principalmente en los siguientes tipos:
Circuito Serie RLC:
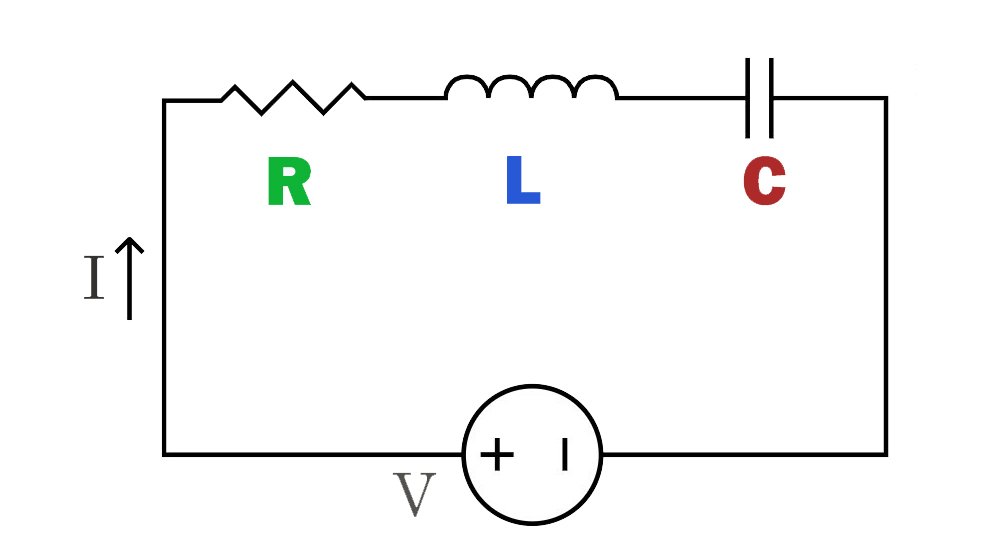
En este circuito, los componentes de resistencia (R), inductor (L) y capacitor (C) están conectados en secuencia en el mismo camino. La corriente pasa a través de la resistencia, el inductor y el capacitor en secuencia, lo que hace que la corriente cambie en consecuencia en cada componente.
El circuito RLC en serie tiene las características de selectividad de frecuencia, presentando diferentes impedancias y características de respuesta a diferentes frecuencias, por lo que se utiliza ampliamente en filtros y circuitos sintonizados.
Circuito Paralelo RLC:
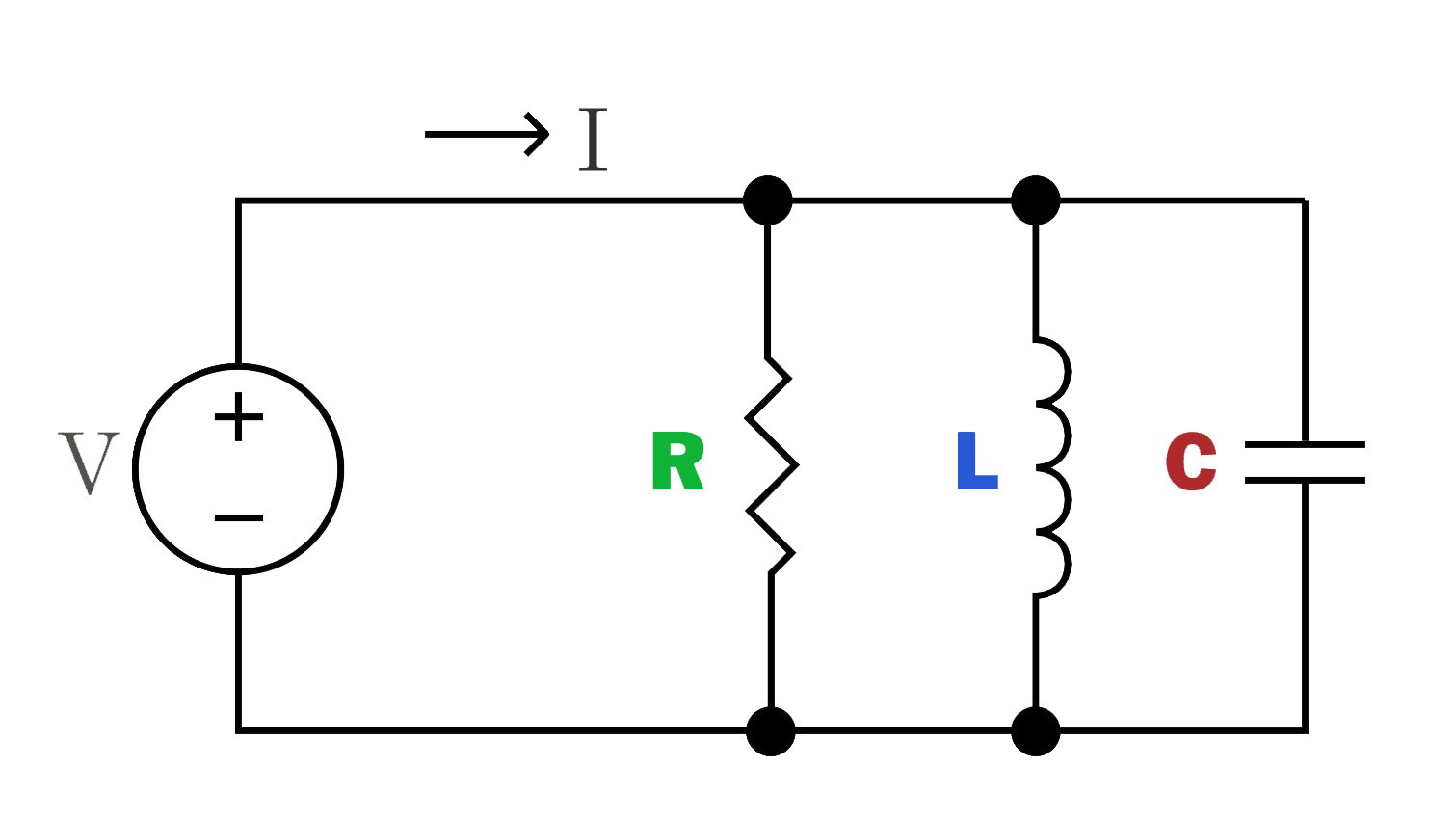
El circuito RLC paralelo es conectar la resistencia, el inductor y el capacitor en caminos paralelos respectivamente. La corriente se divide en las ramas, y el voltaje que pasa a través de cada componente es el mismo.
Este circuito tiene características de impedancia para la corriente a una frecuencia específica, que se puede utilizar para pasar o bloquear selectivamente señales de ciertas frecuencias.
¿Cómo medir el voltaje en el circuito RLC?
Como se muestra en los diagramas de abajo:
Cuando U es un voltaje sinusoidal, este circuito tiene tres puntos potenciales D, E y F. Estas tres formas de onda se pueden observar usando un osciloscopio o medir con un voltímetro de CA para UD, UE, UL, UR y UC. El gráfico dinámico de la derecha refleja los cambios en estos cinco voltajes con el tiempo en un determinado escenario. En el gráfico dinámico, UF es equivalente a UL, e idealmente, debería haber otro voltaje UDF, pero he elegido no incluir voltajes con subíndices de dos letras por simplicidad.
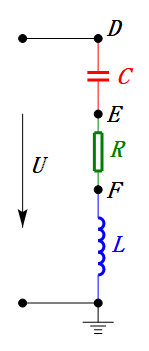
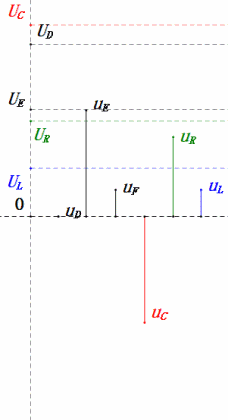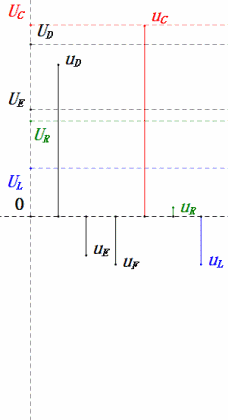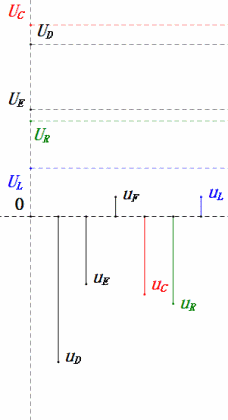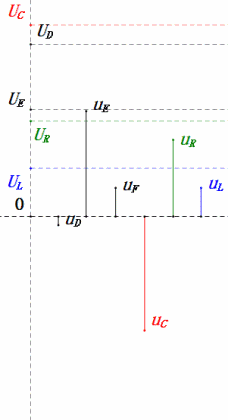
Calculation Formula for Voltage
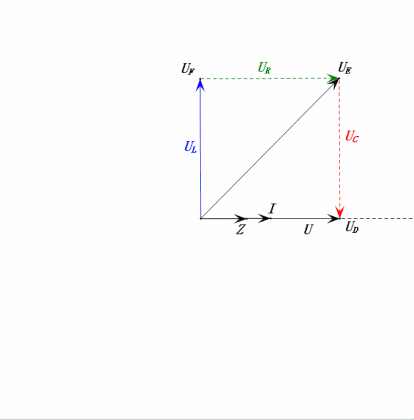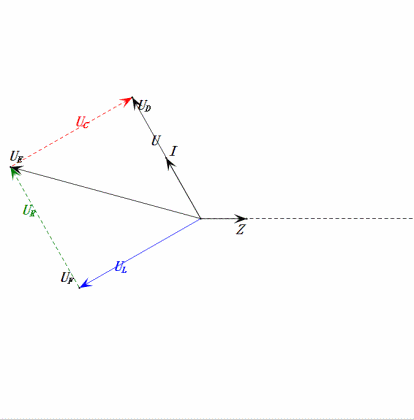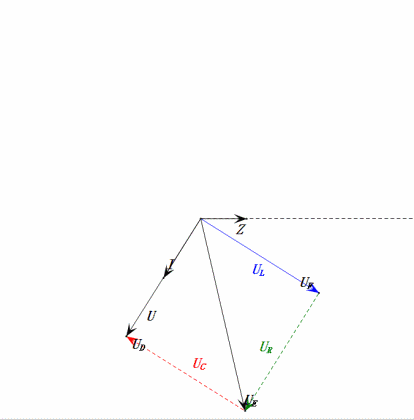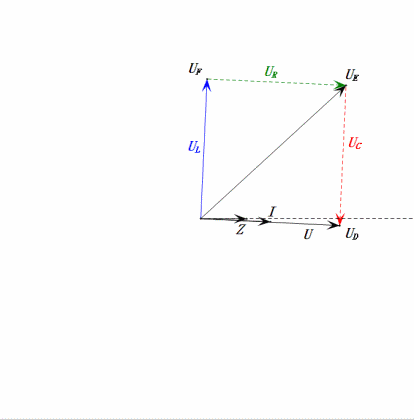
El método del fasor es una solución brillante que facilita la resolución de problemas, pero puede hacernos perdernos los fascinantes procesos dinámicos representados en el gráfico anterior. Con la reactancia inductiva XL, la resistencia R y la reactancia capacitiva XC, el método del fasor para resolver este circuito se describe a continuación:
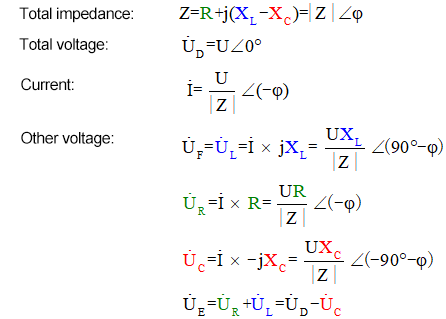
El voltímetro de CA mide UR ≠ UE – UL. Si L es un inductor ideal, estos tres formarán un triángulo rectángulo. De manera similar, UC, UD y UE también formarán un triángulo, aunque no necesariamente rectángulo. Esto no implica que se viole la ley de voltaje de Kirchhoff (KVL). Si se mide el valor instantáneo u en un determinado momento, se encontrará que uR = uE – uL y uC = uD – uE. Además, aunque no se mide la corriente, los cambios en UR están en fase con los cambios en la corriente.
Sine Signal Action and Resonance State
Cuando se aplica una señal sinusoidal, la reactancia inductiva XL = ωL y la reactancia capacitiva XC = (ωC)^-1. El estado en el que estos dos son iguales se conoce como resonancia, lo que nos permite calcular una frecuencia angular de resonancia ω₀.
En la siguiente sección, configuraremos los parámetros para crear diagramas de fasores, diagramas de ondas sinusoidales estáticas y animaciones de los cambios instantáneos del valor del voltaje a 0.5ω₀, ω₀ y 2ω₀.
Voltage under Different Resonant Angular Frequencies
Model Parameters:
- U = 6.00mV
- R = 2.00Ω (corriente efectiva menor a 3.00mA, generalmente seguro para componentes)
- C = 125μF
- L = 0.500mH
Calculado ω = 4000rad/s (correspondiendo a una frecuencia de aproximadamente 637Hz, ignorando los efectos de la radiación electromagnética para conveniencia de modelado. Los diagramas fasoriales y los diagramas de onda sinusoidal utilizan valores RMS; para valores máximos, multiplique por 1.414)
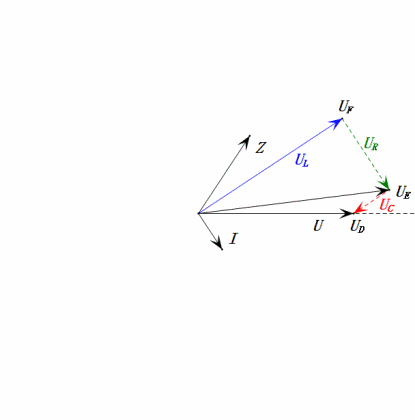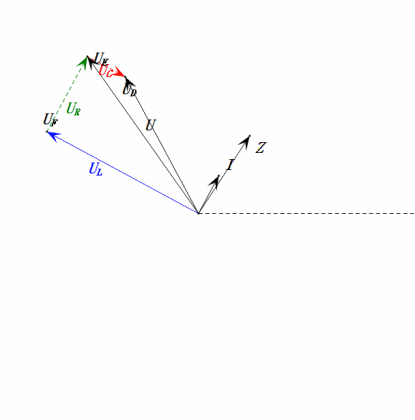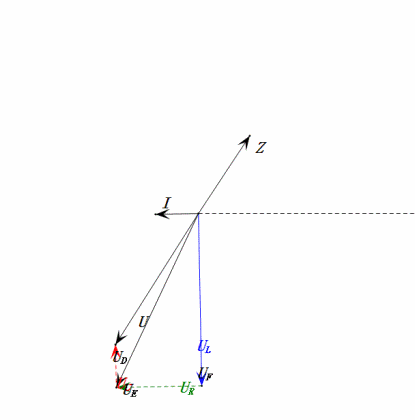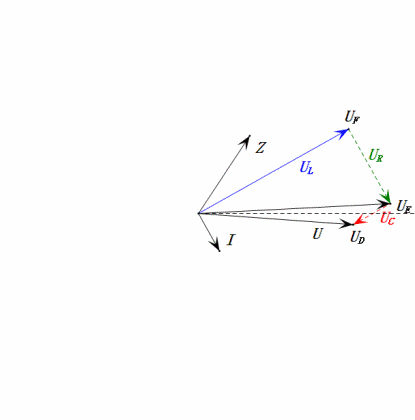
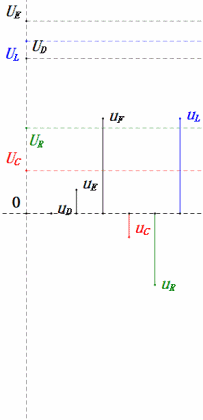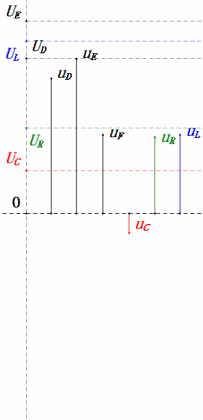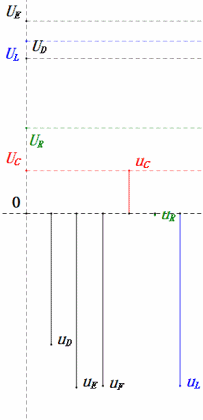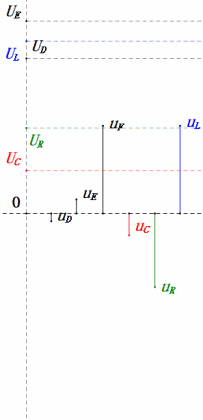
Voltaje dinámico bajo 0.5ω
Después de los cálculos, podemos dibujar el diagrama fasorial y el diagrama de onda sinusoidal estática en el momento inicial:
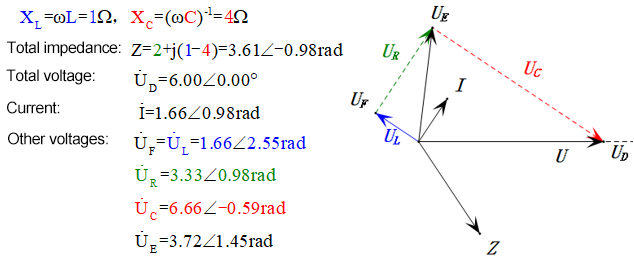
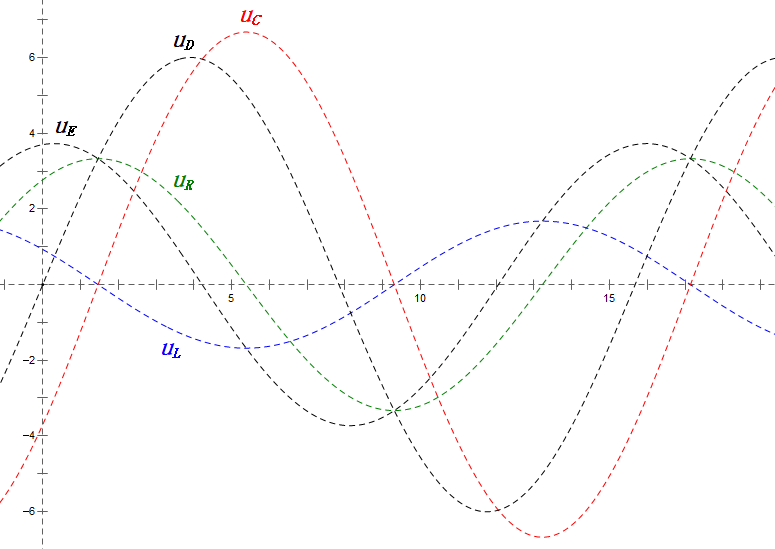
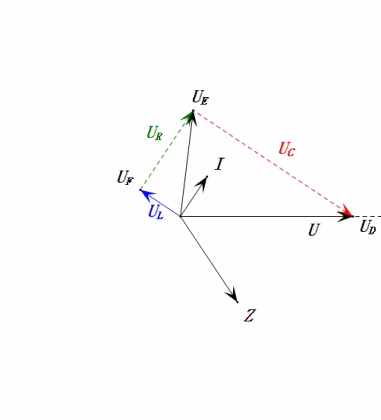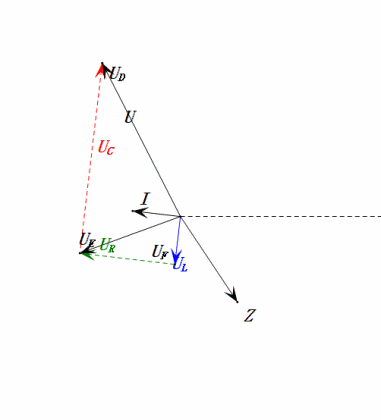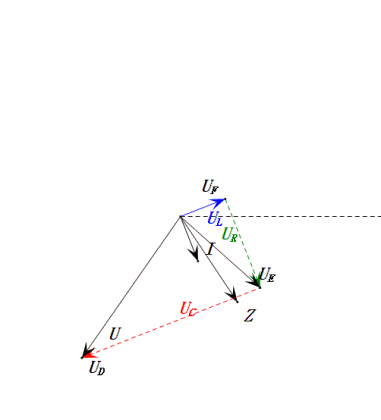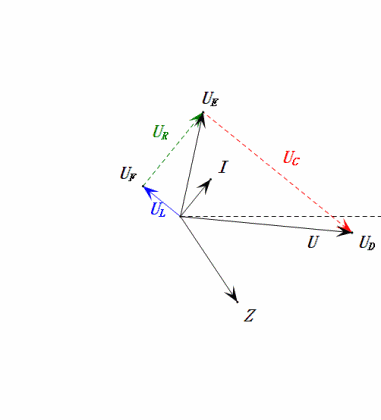
Análisis:
- Corriente máxima ≤ 1.57mA, seguro para componentes.
- El diagrama fasorial forma un trapecio rectángulo sin considerar el UDF.
- A 0.5ω, XL < XC → menor UL, mayor UC. El uC excede el voltaje de la fuente de alimentación, potencialmente dañando el capacitor.
- uC se retrasa en relación con uD por ≈30°. La carga comienza durante la fase ascendente de uD, terminando cuando uR = 0.
- El diagrama de onda sinusoidal muestra uR = uE – uL y uC = uD – uE en cada momento.
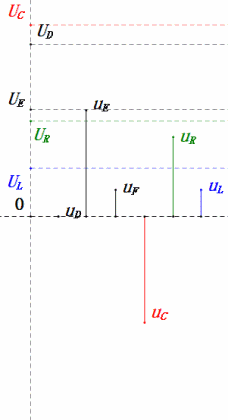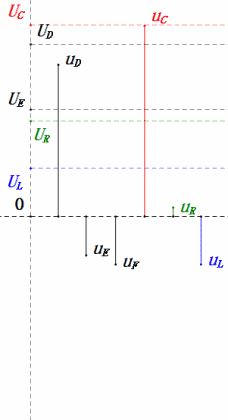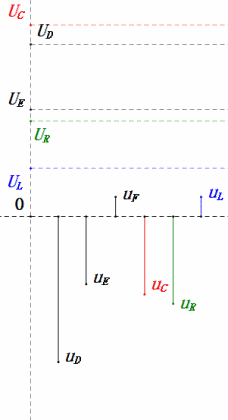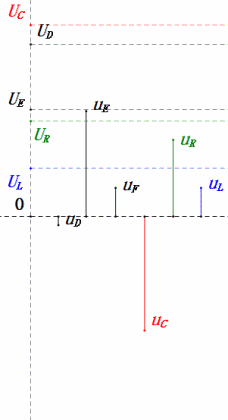
Voltaje dinámico bajo 1ω
Después de los cálculos, podemos dibujar el diagrama fasorial y el diagrama de onda sinusoidal estática en el momento inicial:
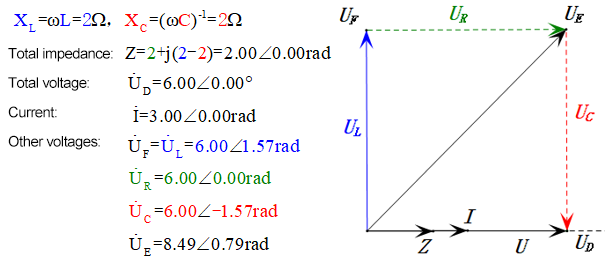
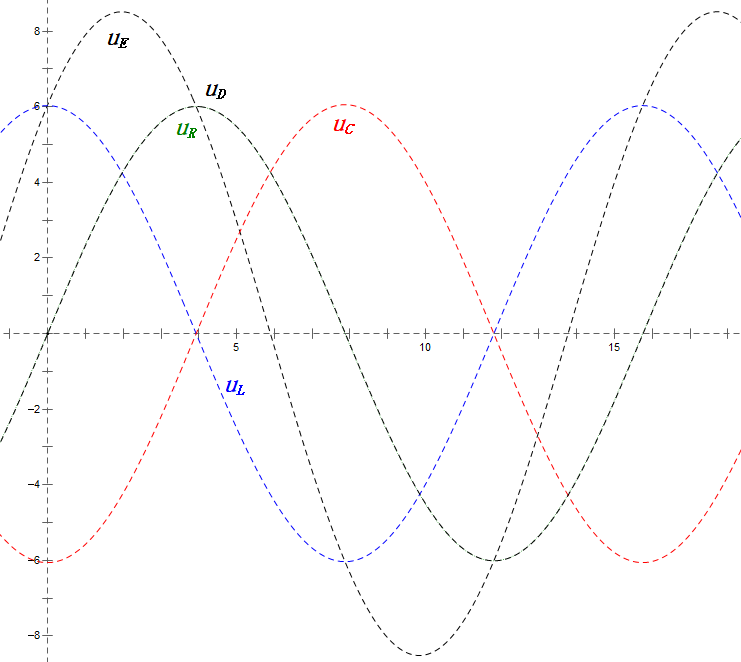
Análisis:
- Corriente máxima ≈ 4.24mA, seguro para los componentes.
- El diagrama fasorial forma un cuadrado en resonancia (XL = XC).
- La tensión uE excede la tensión de alimentación, pero el impacto en el componente no está claro.
- Coincidencia: XL = XC = R → uL y uC se cancelan en el diagrama de onda sinusoidal, pero los cambios de corriente afectan las amplitudes.
- Impedancia minimizada, corriente maximizada en resonancia debido al efecto de «corriente máxima».
- uC se retrasa con respecto a uD exactamente en 90°; la carga comienza cuando uD alcanza su pico y termina cuando uR = uD = 0.
- Los segmentos del diagrama de onda sinusoidal representan la mitad del tiempo del Caso 1.
- Máxima UD = UR, UL = UC debido a los parámetros, pero que todas las cuatro tensiones sean iguales es una coincidencia.
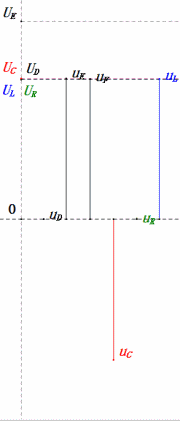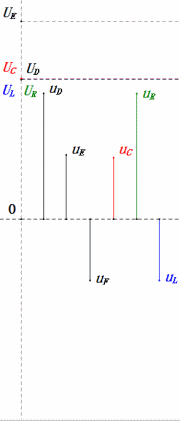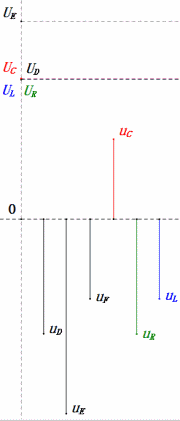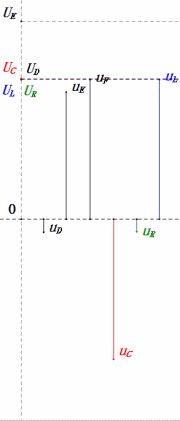
Voltaje dinámico bajo 2ω0
Después de los cálculos, podemos dibujar el diagrama fasorial y el diagrama de onda sinusoidal estática en el momento inicial:
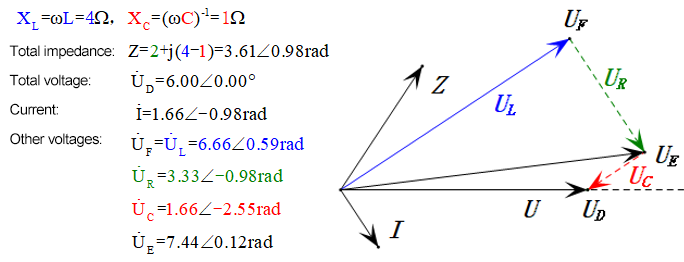
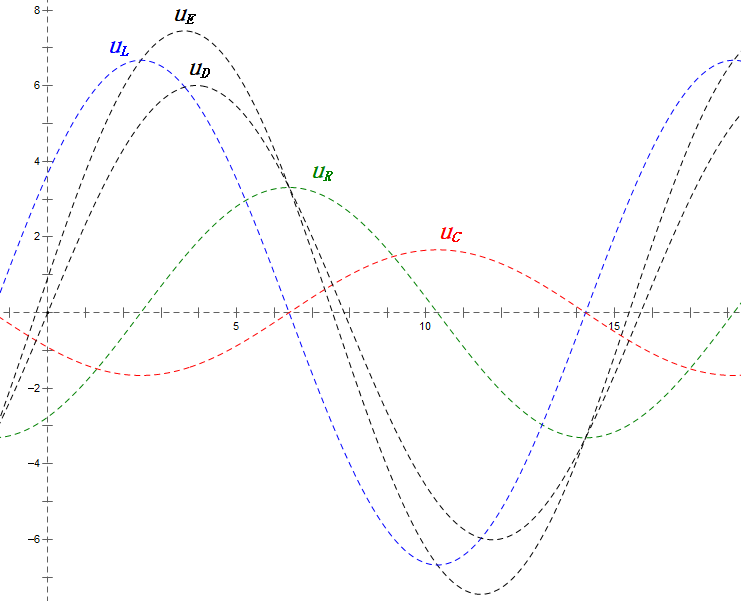
Análisis:
- Corriente máxima ≈ 1.57mA, seguro para los componentes.
- El diagrama fasorial forma un trapecio derecho.
- A 2ω0, XL > XC → UL más grande, UC más pequeño. Máxima uL y uE exceden la tensión de alimentación, lo que genera preocupaciones sobre daños al inductor.
- uC se retrasa con respecto a uD en ≈150°; la carga comienza cuando uD cae a ≈la mitad de su valor máximo, terminando cuando uR = uD = 0.
- Los segmentos del diagrama de onda sinusoidal representan la mitad del tiempo del Caso 2.
- Las ecuaciones uR = uE – uL y uC = uD – uE se cumplen en cada momento.