Что такое цепь RLC?
Цепь RLC — это электрическая цепь, содержащая резистор (R), индуктор (L) и конденсатор (C), соединенные последовательно или параллельно. Эти компоненты работают вместе для хранения и передачи энергии, что приводит к колебаниям с определенной резонансной частотой. Цепи RLC широко используются в различных приложениях, включая фильтры, генераторы и настроечные цепи.
Типы RLC-цепей
Цепи RLC можно разделить на следующие типы:
Цепь серии RLC:
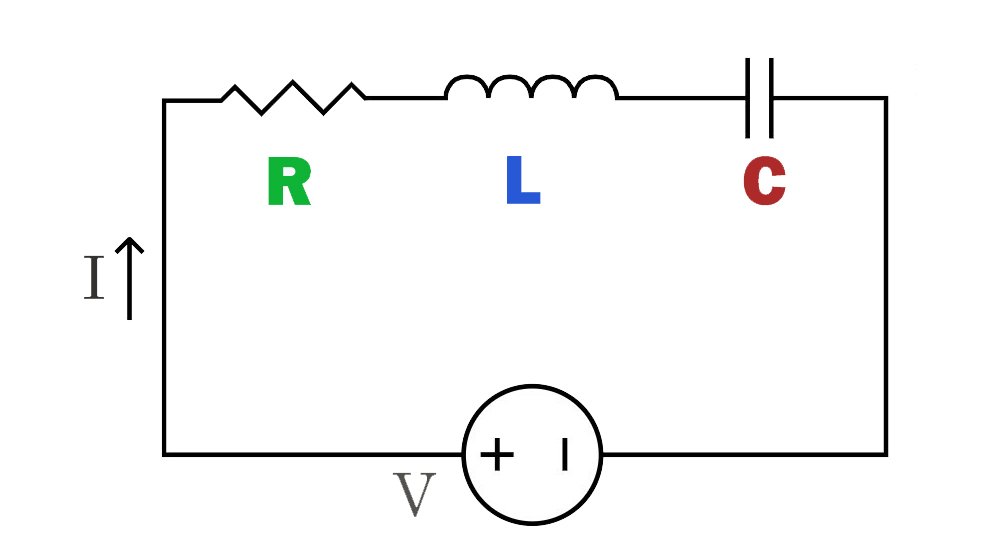
В этой цепи резистор (R), индуктор (L) и конденсатор (C) соединены последовательно на одном пути. Ток проходит через резистор, индуктор и конденсатор последовательно, вызывая соответствующее изменение тока в каждом компоненте.
Последовательная RLC-цепь обладает характеристиками частотной селективности, демонстрируя различные характеристики импеданса и отклика на разных частотах, поэтому она широко используется в фильтрах и настроенных цепях.
Параллельная цепь RLC:
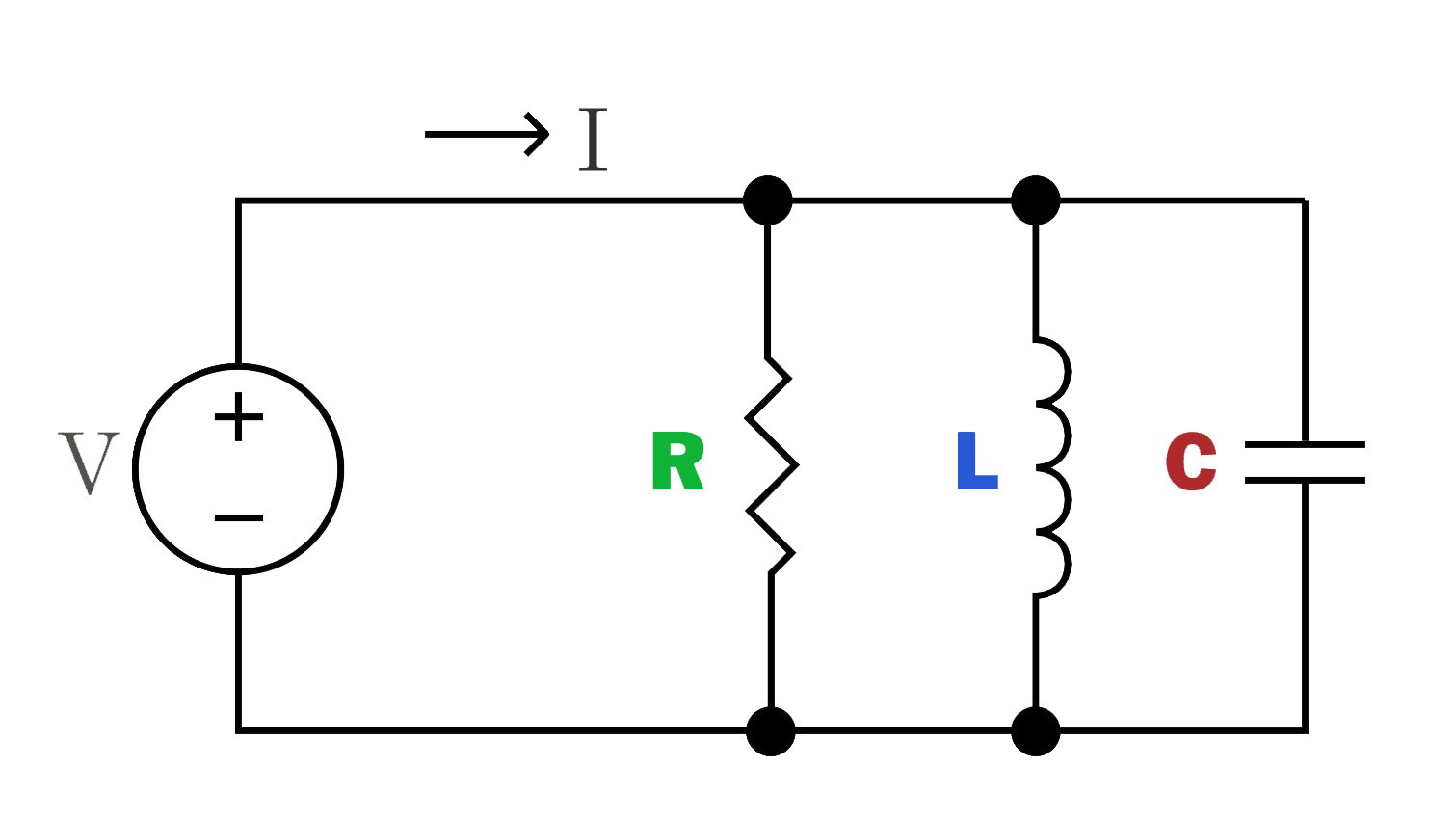
Параллельная цепь RLC состоит из резистора, индуктора и конденсатора, соединенных параллельно. Ток распределяется по ветвям, и напряжение, проходящее через каждый компонент, одинаково.
Эта цепь имеет импедансные характеристики для тока с определенной частотой, что может быть использовано для выборочной пропускания или блокирования сигналов определенных частот.
Как измерить напряжение в RLC-цепи?
Как показано на приведенных ниже схемах:
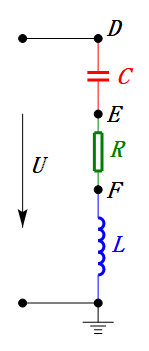
Когда U является синусоидальным напряжением, эта схема имеет три потенциальные точки D, E и F. Эти три формы волны можно наблюдать с помощью осциллографа или измерить с помощью вольтметра переменного тока для UD, UE, UL, UR и UC. Динамический график справа отражает изменения этих пяти напряжений во времени в определенном сценарии. На динамическом графике UF эквивалентно UL, и в идеале должно быть еще одно напряжение UDF, но для простоты я решил не включать напряжения с двухбуквенными индексами.
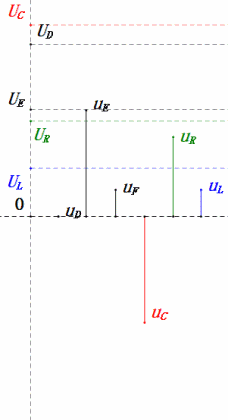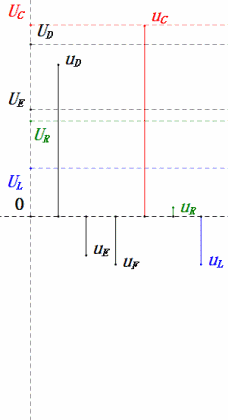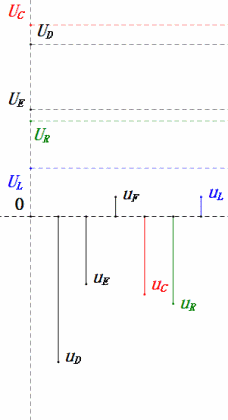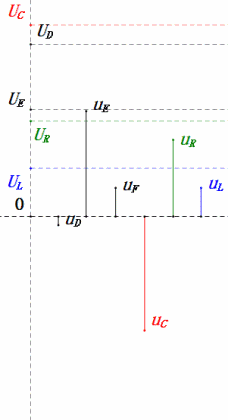
Формула расчета напряжения
Фазорный метод — это блестящее решение, которое облегчает решение задач, но может привести к тому, что мы упустим из виду увлекательные динамические процессы, изображенные на графике выше. С индуктивным сопротивлением XL, сопротивлением R и емкостным сопротивлением XC фазорный метод решения этой схемы выглядит следующим образом:
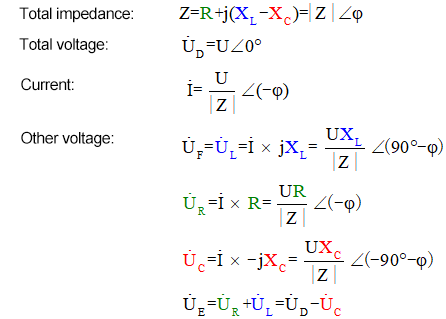
Вольтметр переменного тока измеряет UR ≠ UE — UL. Если L является идеальным индуктором, эти три элемента образуют прямоугольный треугольник. Аналогично, UC, UD и UE также образуют треугольник, хотя и не обязательно прямоугольный. Это не означает, что нарушается закон Кирхгофа (KVL). Если измерить мгновенное значение u в определенный момент времени, то будет обнаружено, что uR = uE — uL и uC = uD — uE. Кроме того, хотя ток не измеряется, изменения UR синхронизированы с изменениями тока.
Действие синусоидального сигнала и состояние резонанса
При подаче синусоидального сигнала индуктивное сопротивление XL = ωL, а емкостное сопротивление XC = (ωC)^-1. Состояние, при котором эти два сопротивления равны, называется резонансом, что позволяет рассчитать резонансную угловую частоту ω0.
В следующем разделе мы установим параметры для создания фазорных диаграмм, статических синусоидальных диаграмм и анимаций мгновенных изменений напряжения при 0,5ω0, ω0 и 2ω0.
Напряжение при различных резонансных угловых частотах
Параметры модели:
- U = 6,00 мВ
- R = 2,00 Ом (эффективный ток менее 3,00 мА, в целом безопасен для компонентов)
- C = 125 мкФ
- L = 0,500 мГн
Рассчитанное ω0 = 4000 рад/с (соответствует частоте примерно 637 Гц, без учета эффектов электромагнитного излучения для удобства моделирования. В фазорных диаграммах и диаграммах синусоидальных волн используются среднеквадратичные значения; для получения пиковых значений умножьте на 1,414).
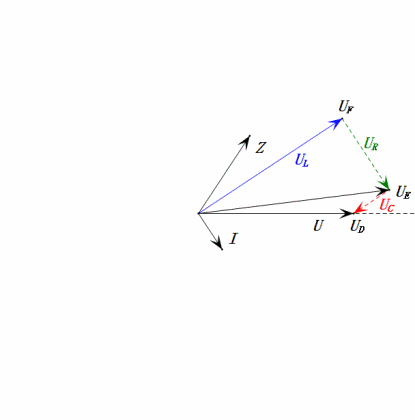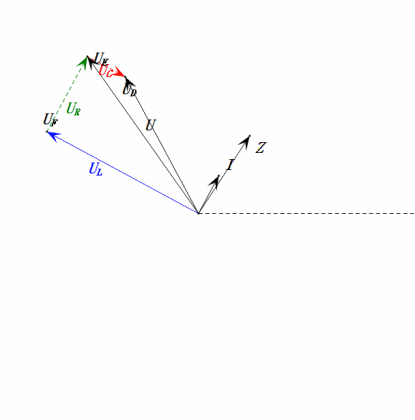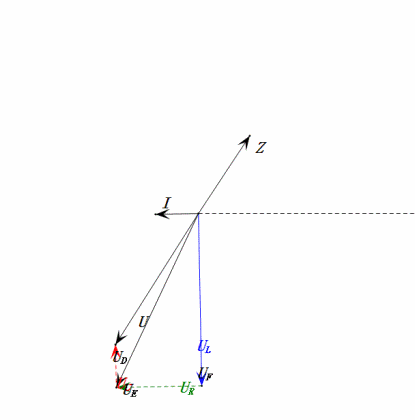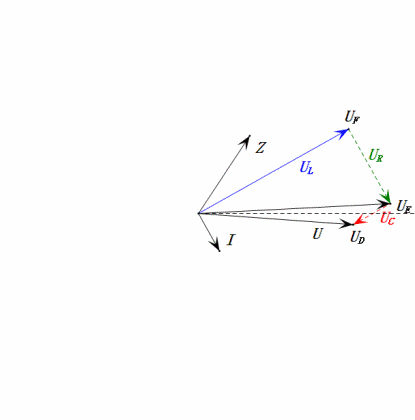
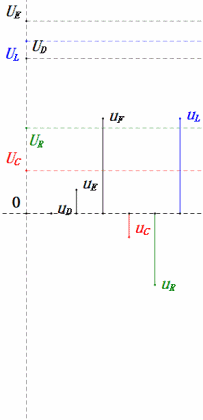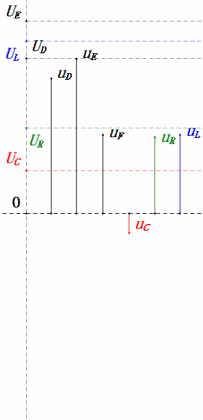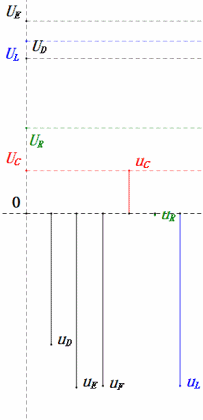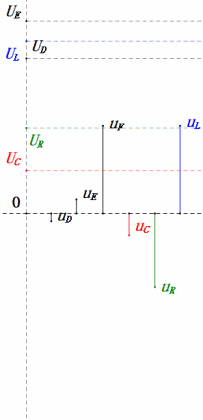
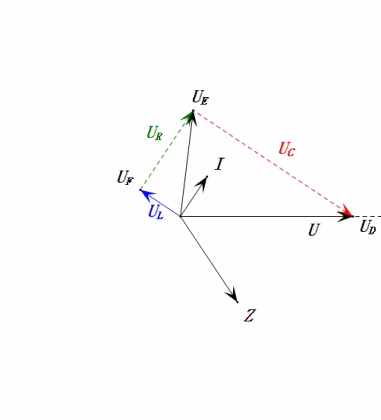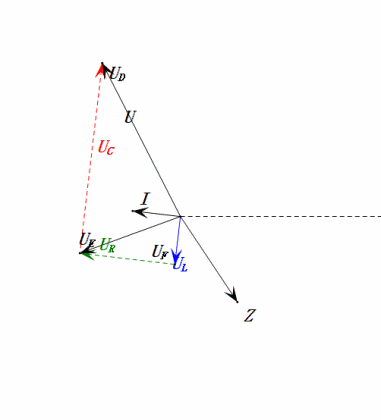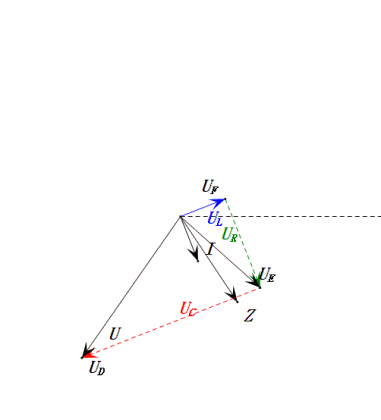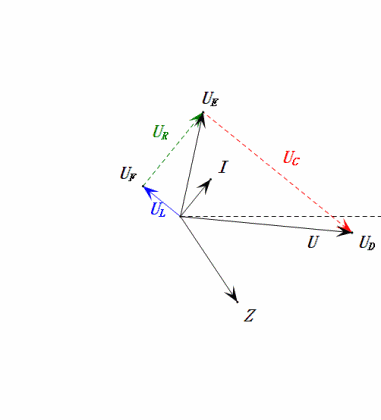
Динамическое напряжение при 0,5 Ом
После расчетов мы можем построить фазорную диаграмму и статическую синусоидальную диаграмму в начальный момент:
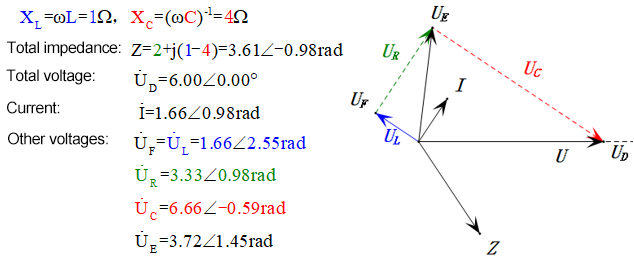
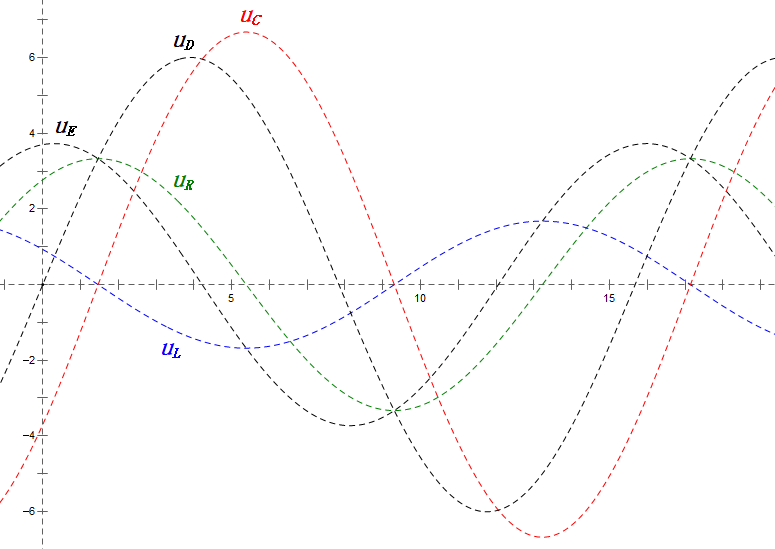
Анализ:
- Максимальный ток ≈ 1,57 мА, безопасный для компонентов.
- Фазорная диаграмма образует правильную трапецию без учета UDF.
- При 0,5 Ом, XL < XC → меньшее UL, большее UC. Максимальное uC превышает напряжение источника питания, что может повредить конденсатор.
- uC отстает от uD на ≈30°; зарядка начинается во время фазы нарастания uD и заканчивается, когда uR = 0.
- Синусоидальная диаграмма показывает, что uR = uE — uL и uC = uD — uE в каждый момент времени.
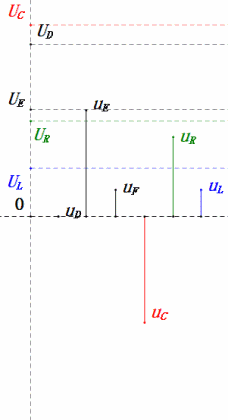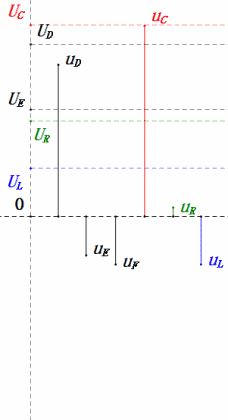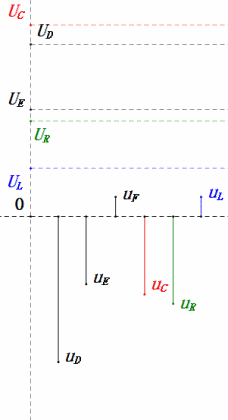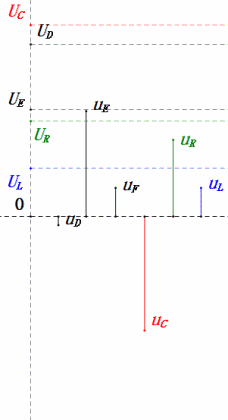
Динамическое напряжение при 1ω0
После расчетов мы можем построить фазорную диаграмму и статическую синусоидальную диаграмму в начальный момент:
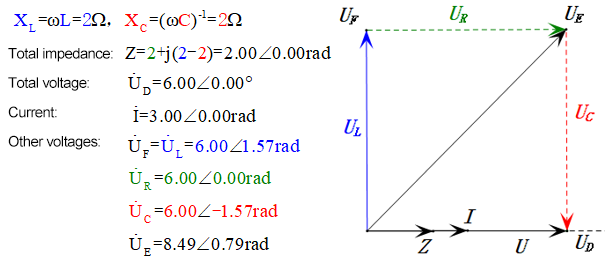
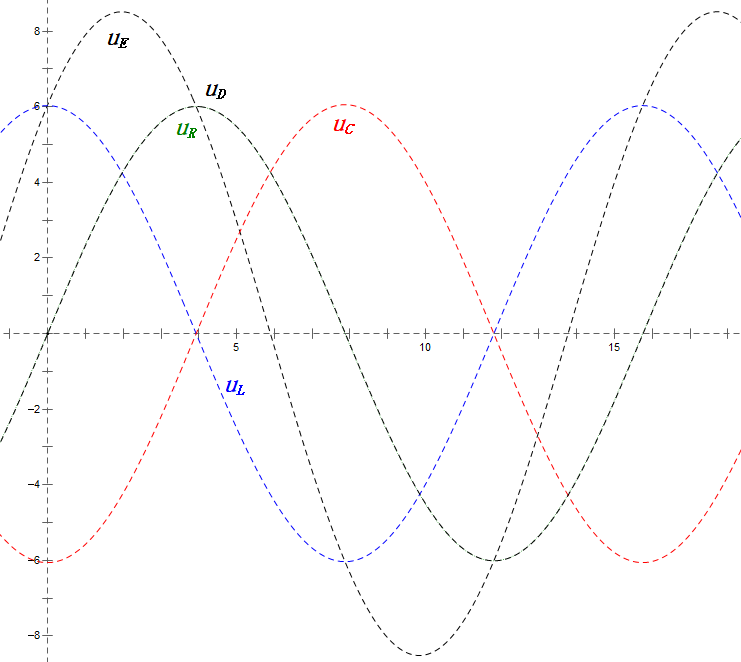
Анализ:
- Максимальный ток ≈ 4,24 мА, безопасный для компонентов.
- Фазорная диаграмма образует квадрат при резонансе (XL = XC).
- Максимальное uE превышает напряжение источника питания, но влияние на компоненты неясно.
- Совпадение: XL = XC = R → uL и uC взаимно компенсируются в синусоидальной диаграмме, но изменения тока влияют на амплитуды.
- Импеданс минимизирован, ток максимизирован при резонансе из-за эффекта «максимального тока».
- uC отстает от uD ровно на 90°; зарядка начинается, когда uD достигает пика, и заканчивается, когда uR = uD = 0.
- Сегменты синусоидальной диаграммы представляют половину времени случая 1.
- Максимальное UD = UR, UL = UC из-за параметров, но равенство всех четырех напряжений является совпадением.
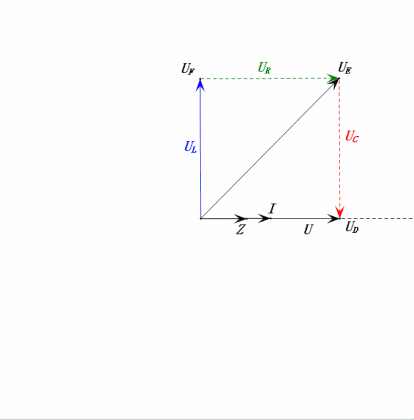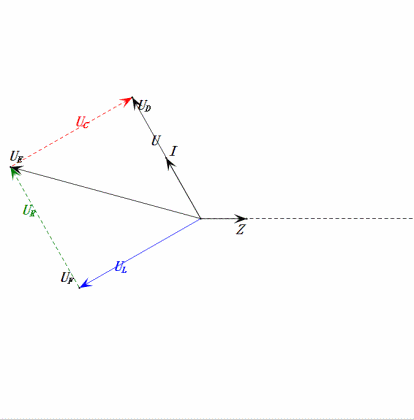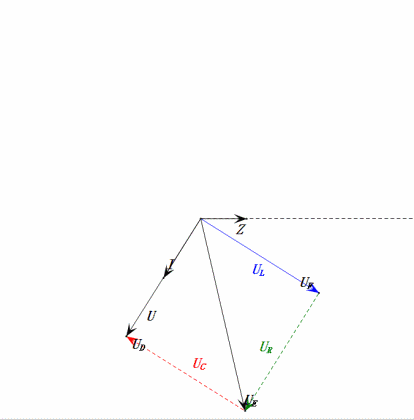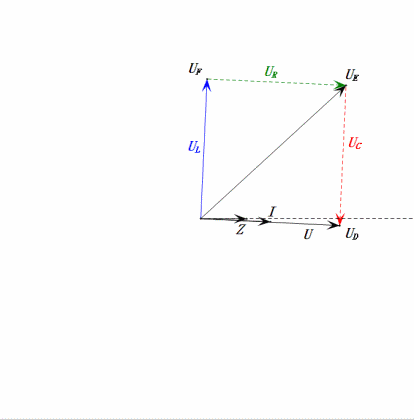
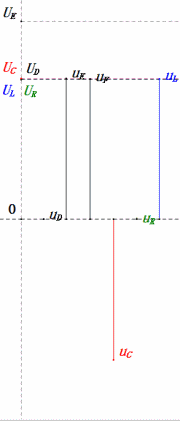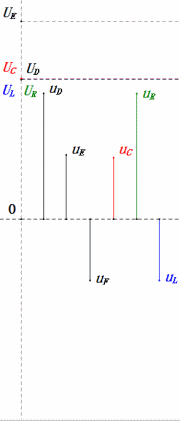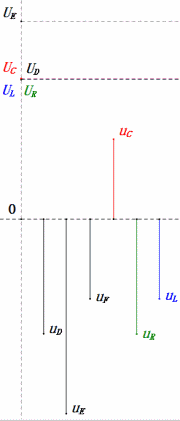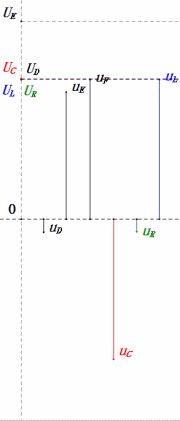
Динамическое напряжение при 2ω0
После расчетов мы можем построить фазорную диаграмму и статическую синусоидальную диаграмму в начальный момент:
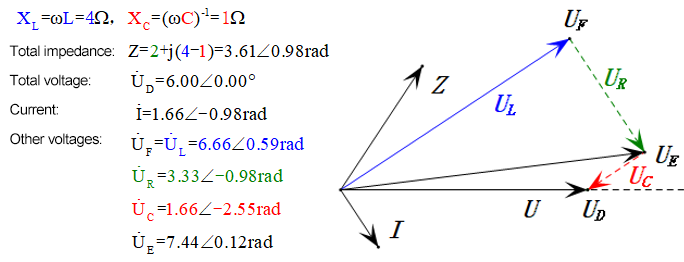
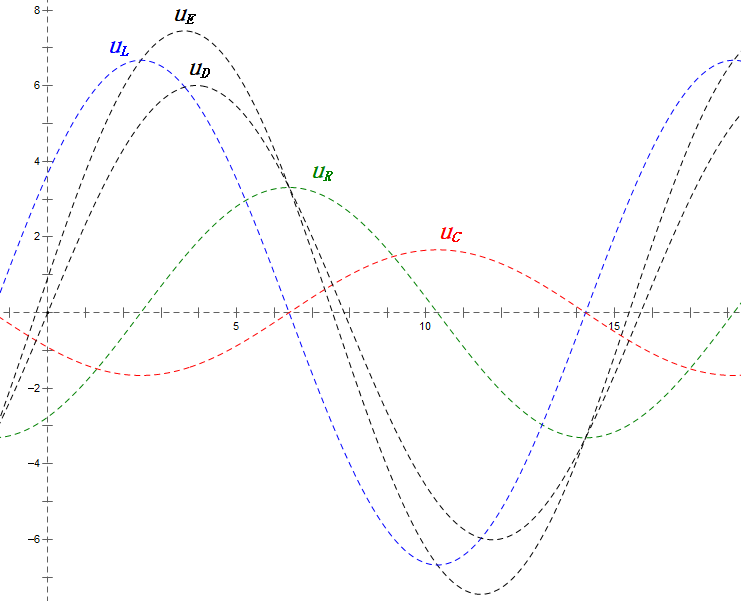
Анализ:
- Максимальный ток ≈ 1,57 мА, безопасный для компонентов.
- Фазорная диаграмма образует правильную трапецию.
- При 2ω0, XL > XC → больше UL, меньше UC. Максимальные значения uL и uE превышают напряжение источника питания, что вызывает опасения по поводу повреждения индуктора.
- uC отстает от uD на ≈150°; зарядка начинается, когда uD падает до ≈половины своего максимального значения, и заканчивается, когда uR = uD = 0.
- Сегменты синусоидальной диаграммы представляют половину времени случая 2.
- Уравнения uR = uE — uL и uC = uD — uE верны в каждый момент времени.